Para o pórtico abaixo determine o sistema de equações completo que devemos resolver para determinação dos seus esforços.
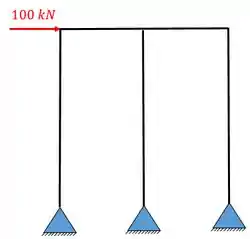
Passo 1
Fala, pessoal!! Vamos resolver um exercício aqui sobre método das forças. Esse problema não pede para acharmos o resultado final (valor das reações nos apoios), pede apenas para encontrarmos as equações que nos levarão a esse resultado, beleza?
Para achar essas equações a gente tem que lembrar de dividir esse problema hiperestático em problemas isostáticos, que são mais simples. Além disso, vamos ter de utilizar aquele conceito das deformações:

Esse conceito é a parte fundamental do nosso problema e saber utilizá-lo corretamente fará toda a diferença!
Então vamos seguir nosso passo a passo para resolver com calma.
Passo 2
Para podermos saber como montar o nosso sistema, precisamos em primeiro lugar saber quantos termos nosso sistema vai ter, e já sabemos que isso vai ser dado pelo número de hiperestáticos, então o que precisamos fazer é determinar o número de hiperestáticos do nosso problema.
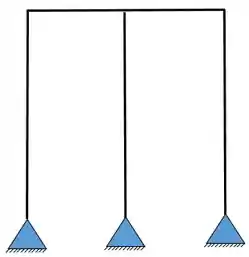
- Hiperestáticos totais pelo macete
- Sabemos que temos 3 apoios do segundo gênero, totalizando 6 incógnitas externas
- Não temos regiões fechadas, totalizando 0 incógnitas internas
- Temos 3 equações de equilíbrio
- Não temos rótulas
Ou seja, nossa estrutura possui um grau de hiperestaticidade, sendo assim, nós precisamos abaixar dois graus da nossa estrutura, transformando-a em uma estrutura em isostática. É exatamente isso que vamos fazer, e é aqui que mora o segredo, podemos quebrar quaisquer dois vínculos da nossa estrutura, desde que ela fique isostática (ou seja, a nossa estrutura deve permanecer em equilíbrio, não pode cair kkkk).
Passo 3
Para obter uma estrutura isostática vamos fazer o seguinte: retirar completamente um dos apoios e colocar duas forças (uma horizontal e outra vertical) em seu lugar; e transformar o outro apoio num apoio de primeiro gênero com uma força horizontal. Sendo assim vamos ter o seguinte:
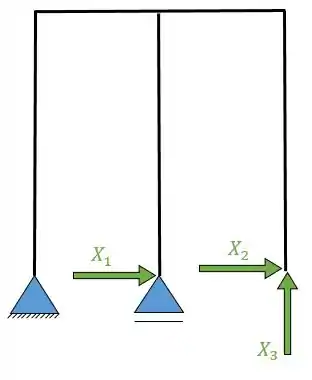
Onde os hiperestáticos são , e .
Passo 4
O próximo passo é bem importante, porque consiste em determinar o número de sistemas que vamos ter que trabalhar. O número de sistemas é dado pela fórmula
Com isso fica bem simples determinar o nosso número de sistemas, pois no passo anterior já determinamos o nosso número de hiperestáticos.
Com isso teremos:
Sabemos que um dos sistemas é o nosso sistema principal, ou como gosto de chamar, sistema zero, onde está o nosso carregamento. Mostrando os sistemas vamos ter:
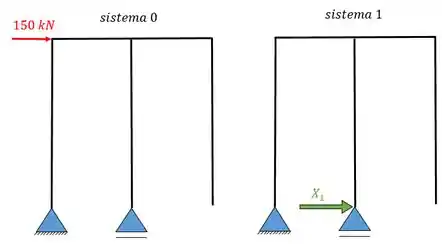
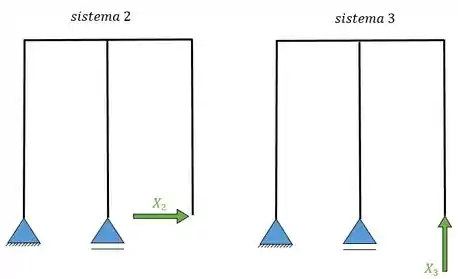
Passo 5
Agora precisamos lembrar como definir a nossa equação, sabemos que o formato segue o seguinte padrão
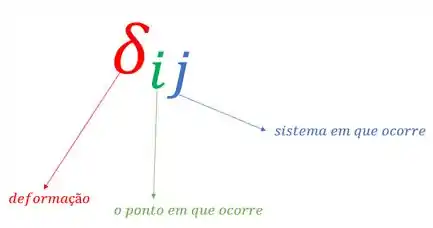
E sabemos que como liberamos a estrutura para se movimentar, sendo que ela não possuía esse movimento, precisamos garantir que o que ocorre nos sistemas 0, 1, 2 e 3 irão se anular.
As nossas equações então vão relacionar o ponto com o sistema. Numerando os apoios de 1, 2 e 3 da esquerda para a direita vamos ter.
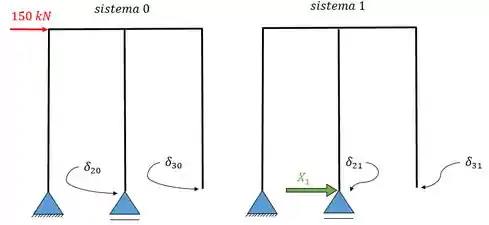
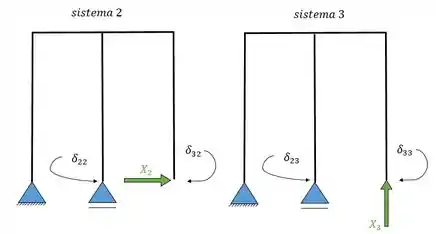
Repare que não temos nenhuma deformação no apoio de segundo gênero, isso acontece porque esse tipo de apoio não permite deformação. Sendo assim vamos ter apenas os seis relacionados acima.
Passo 6
Pessoal, a gente tem que lembrar que o nosso é uma deformação unitária, enquanto os nossos hiperestáticos são as cargas reais. Então a deformação real, que é nula, é dada pela soma de cada parte:
Como dividimos o problema a soma de cada parte tem que ser igual ao problema original. Sendo assim vamos ter:
Pessoal, tão vendo que tem duas equações praticamente iguais? Isso acontece porque no ponto 3 existem dois tipos de deslocamento, o horizontal e o vertical, sendo assim, vamos ter duas equações distintas onde os de uma são diferentes da outra.
Perceba que para o sistema zero não há hiperestático.