Um tanque de mistura mostrado na figura seguinte com volume de líquido e densisdade constante é usado para misturar duas correntes.
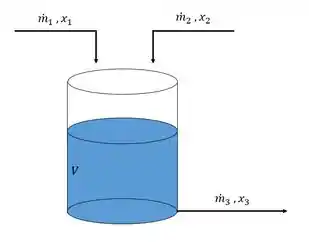
- Assuma que o processo está operando por um longo período de tempo com uma vazão mássica de entrada de e e composição das correntes de entrada de e . Nesse contexto, qual é o estado estacionário de ?
- Desenvolva o modelo matemático do sistema supondo que o nível de líquido possa variar.
Passo 1
Para determinar a composição de saída, precisamos fazer o balanço de massa para o componente.
Não existe reação no processo, portanto os termos de reação e consumo serão nulos. Além disso, também não existe acúmulo porque o enunciado diz que o volume não vatia e as composições são constantes.
Portanto:
Sabendo que as correntes e são as correntes de entrada e a corrente é a corrente de saída, teremos:
Substituindo os valores do enunciado:
Passo 2
Primeiramente vamos fazer o modelo para o volume de líquido no tanque. Vamos fazer o balanço de massa geral:
Novamente não temos reação, portanto sem acúmulo e sem geração:
Fazendo:
Como é constante, podemos passar ele dividinfo para o outro lado:
Passo 3
Vamos fazer agora o modelo matemático para a composição de saída . Para isso, devemos considerar que o modelo está em parâmetros concentrados, ou seja, o tanque é perfeitamente misturado e a composição no interior do tanque é igual à composição da saída. Vamos partir da expressão de balanço de massa geral que encontramos no passo anterior:
Agora vamos escrever o balanço de massa por componente:
Vamos aplicar a regra do produto no termo do acúmulo:
Substituindo no balanço:
Rearranjando:
Como:
Podemos substituir no balanço:
Vamos cortar que da pra cortar:
Por fim:
Se você quiser escrever as respostas em termos de volume, é só substituir por :
Resposta
a)
b)