Introdução a Bombas
Teoria
Máquinas de fluxo
Antes de falar especificamente de bombas, queria fazer um comentário geral sobre máquinas de fluxo, porque esse termo é importante, ok?
Máquinas de fluxo são máquinas que adicionam ou retiram energia de um fluido. Aqui embaixo tem um resumo das classes de máquinas e quando são usadas:
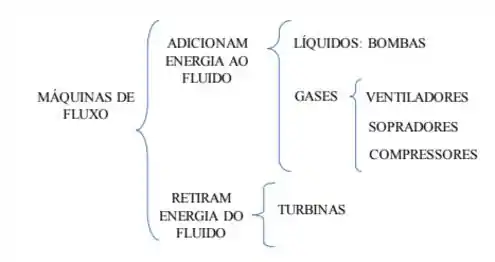
O nosso foco maior agora são as bombas.
Bombas
Chegou a hora de falar de bombas!
Ops, essas não!
Bombas são máquinas de fluxo que fornecem energia a um fluido INCOMPRESSÍVEL, ou seja, líquidos. Esse aumento de energia resulta em aumento de PRESSÃO, mas não necessariamente de velocidade, ok?
Podemos classificar as bombas pela forma que essa energia é transferida ao líquido:
- Bombas Dinâmicas (ou Turbobombas)
- Bombas de deslocamento positivo (ou volumétricas)
Mas antes de falar um pouco delas, bora entender melhor a estrutura de uma bomba. Por enquanto, queria que você soubesse de três partes principais:
- Bocal de sucção, que é por onde o fluido entra na bomba
- Carcaça da bomba, que é a estrutura externa dela como um todo
- Bocal de descarga (ou recalque), que é por onde o líquido sai
Bombas Dinâmicas ou Turbobombas
Nas turbobombas, a energia é fornecida ao fluido por meio de um impelidor (ou impulsor, ou rotor) que vai aumentar a energia cinética do fluido e depois vai ser transformada em energia de pressão. E, antes que você me bata, deixa eu explicar melhor esse lance de impelidor haha. Dá uma olhada nessa imagem:
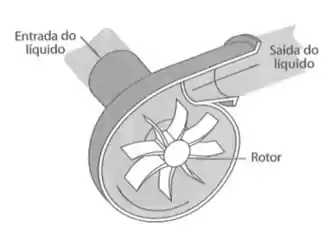
Pra ajudar a visualizar, pensa como se fosse a hélice de um navio. Enfim, um detalhe é que, como tá na figura aí de cima, o fluido entra na carcaça da bomba no sentido axial e só depois começa o giro, isto é, movimento radial em direção à saída.
Dentro de turbobombas, vou destacar a mais falada: a bomba centrífuga. Nelas, a energia cinética vem somente de forças centrifugas que atuam no líquido. Uma vantagem delas é uniformidade da pressão do líquido de saída, sem pulsações.
Bombas de Deslocamento Positivo
Lá nas turbobombas, vimos que a energia transferida ao fluido primeiro era transformada em energia cinética e só depois em energia de pressão. Em bombas de deslocamento positivo, NÃO tem essa passagem pela energia cinética; aqui, a energia é transferida por variação do volume do fluido dentro da própria bomba!
Um exemplo disso são bombas com pistões:
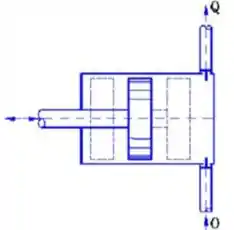
Carga líquida da bomba
A gente viu que as bombas fornecem energia pra um fluido, mas quanta energia? Temos que saber isso, concorda?
Os limites de controle que utilizamos quando trabalhamos com bombas são os locais de entrada e saída do fluido, ou seja, os bocais de sucção e descarga. Fazendo um balanço de energia pro fluido entre os pontos 1 (bocal de sucção) e 2 (bocal de saída):
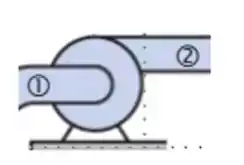
Matematicamente:
Em que:
Se eu estiver falando grego, talvez seja melhor você dar uma olhada, antes de continuar, nos balanços em Mecânica do fluidos, que também estão disponíveis aqui no Responde Aí : )
Continuando, vamos dividir cada termo desse balanço pela gravidade (). Além disso, vamos zerar o termo de atrito; o porquê disso eu te explico daqui a pouco. Relaxa aí.
TODOS os termos que aparecem nessa equação aí de cima têm unidade de comprimento! Todos! Adotando o SI: metro. E, talvez, você precise saber os nomes alguns desses termos:
Mas, sem dúvida, o que você com certeza vai ter que saber é o , que é representado por .
Chamamos de “altura” porque tem unidade de comprimento haha ajuda a lembrar. Outro nome que podemos usar pro é carga líquida da bomba; o porquê desse nome vem lá daquele zerar o termo de atrito que eu fiz, lembra?
É porque a bomba vai dar uma carga pro fluido, mas também vai ter, inevitavelmente, atrito dentro da bomba. Ao zerar o termo de atrito, você tá pegando só a parcela da carga dada que o fluido realmente aproveita.
Curva característica da bomba
A curva característica de uma bomba nada mais é do que uma curva que mostra como a carga fornecida pela bomba () varia com a vazão volumétrica passando pela bomba (). Essas curvas são tipo assim:
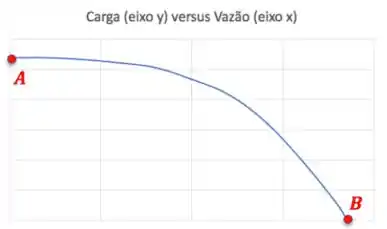
Repara que quanto maior a vazão passando pela bomba, menor a carga fornecida por ela. Mas para vazões baixas, a carga é aproximadamente constante com a vazão. E eu destaquei dois pontos importantes na curva:
Carga de fechamento é a carga fornecida pela bomba quando a vazão é “zero” e vazão de fornecimento livre é a vazão acima da qual nenhuma carga líquida é fornecida.
Curva Característica do Sistema
Assim como podemos obter uma curva para a bomba, podemos obter uma curva característica para um sistema.
Usando o balanço de energia no sistema. Pegando dois pontos quaisquer, 1 e 2, o balanço de energia fica:
Dividindo pela gravidade e rearranjando de forma a isolar o :
é a carga fornecida pela bomba e o termo em vermelho é o , isto é, a carga que o sistema precisa pra funcionar como você quer, com tais velocidades, pressões etc nesses dois pontos.
Se formos plotar versus vazão volumétrica , a gente vai ver que a cara dessa curva é sempre subindo, isto é, quanto maior a vazão, maior a carga requerida pelo sistema.
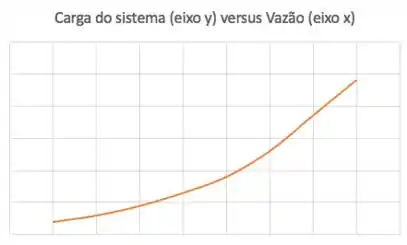
E isso é bem intuitivo. Quanto maior a vazão, maiores as perdas por atritos na tubulação e em cada acidente, então maior será a carga requerida pelo sistema.
Você vai, então, utilizar uma bomba capaz de dar ao seu sistema a carga requerida por ele.
Como o balanço de energia já sugere, o ponto de operação é quando:
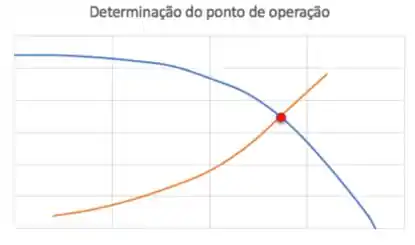
A vazão do ponto de operação é a vazão de operação (nome criativo, né? Haha). E se a bomba é adequada, a vazão de operação é próxima daquela requerida no projeto inicial.
Bombas Dinâmicas ou Turbobombas
Bombas de Deslocamento Positivo
Carga líquida da bomba
Curva característica da bomba
Curva Característica do Sistema
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Bombas são usadas para dar energia, em forma de pressão a fluidos incompressíveis, que é o caso dos líquidos. Diferencie bombas dinâmicas de bombas de deslocamento positivo.
Passo 1
Nas bombas dinâmicas (também conhecidas como turbobombas), a energia é fornecida ao fluido por meio de um impelidor, que vai aumentar a energia cinética do fluido e depois é transformada em energia de pressão.
Já em bombas de deslocamento positivo, NÃO tem essa passagem pela energia cinética; nelas, a energia é transferida por variação do volume do fluido dentro da própria bomba. Um exemplo disso são bombas com pistões.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Elaboração própria
Calcular a carga fornecida por uma bomba centrífuga minerva para um fluido escoando a em uma tubulação de de diâmetro interno.
Dado:
Passo 1
Lá na teoria a gente viu que a carga fornecida por uma bomba centrífuga varia com a vazão de fluido, certo? Temos aqui dados da carga fornecida em diferentes vazões; podemos plotar esses pontos e achar a curva característica da bomba.
Também sabemos a velocidade do fluido e podemos calcular a área transversal da tubulação, já que temos o diâmetro interno.
Como vazão volumétrica é:
Passo 2
Agora que temos a vazão, é só plotar a curva característica da bomba com os dados que temos e pegar o ponto correspondente à . Plotando:
Aí é só ver qual a carga quando à :
Daí carga é:
Passo 3
Uma vez que a gente encontrou , uma forma mais aproximativa de resolver a questão é fazendo uma “regressão linear” dos pontos e . Ou seja, fazer a média dos valores de dados para essas vazões:
Os dois resultados têm um erro associado às aproximações feitas.
Resposta
Exercício Resolvido #3
Elaboração própria
Duas bombas estão disponíveis para determinado projeto e deseja-se selecionar a mais adequada. Sabendo que a vazão desejada ao projeto é e tendo o comportamento das cargas das bombas e do sistema com diferentes vazões, selecione.
Passo 1
Pra fazer essa questão, você tem que lembrar que a vazão de operação de uma bomba é quando a curva da bomba e a curva do sistema se cruzam.
Vamos plotar essas curvas com os dados que nos foram fornecidos e avaliar qual a bomba tem vazão de operação mais próxima de
Passo 2
Repara que a vazão de operação da bomba 1 é mais próxima da vazão de projeto do que a vazão de operação da bomba 2 .
Mas, além disso, tem um detalhe muito importante: ter a próxima da é o norte pra você se aproximar da bomba ideal ao seu projeto quando há várias opções, mas temos sempre que escolher de forma a superprojetar a bomba, caso não seja possível a exatidão.
O que quero dizer com isso é, caso não dê para escolher uma bomba em que , então escolha . Dessa forma, caímos sempre numa situação em que , ou seja, a carga fornecida é maior do que a carga necessária.
Então, escolhe-se a bomba 1.
Para que a vazão seja correta, vamos utilizar uma válvula logo depois da bomba, que controle essa vazão!
Resposta
Bomba 1
Exercício Resolvido #4
Concurso Petrobras 2011 - Eng. Proc. Júnior
Em uma refinaria, uma bomba será responsável por transportar água entre duas lagoas de aeração, ao longo de uma tubulação de de comprimento e de diâmetro. Não há diferença de elevação entre os pontos de captação e descarga da água. No escoamento, através da tubulação, o fator de atrito de Darcy pode ser estimado como . Para executar essa tarefa, está sendo avaliada a possibilidade da utilização de uma bomba com a seguinte curva característica:
onde H é a carga hidráulica em metros e q é a vazão volumétrica em . Considerando-se a aceleração da gravidade como , a relação entre o comprimento e o diâmetro da circunferência como 3 e desprezando-se as perdas de carga localizadas, a vazão de operação do sistema corresponderá à solução da seguinte equação algébrica:
Passo 1
O enunciado é grande, mas a resolução é de boas, ainda que meio longa. É só lembrar do balanço de energia:
No balanço de energia aparece , mas o enunciado dá informação de ; ou divido tudo por ou multiplico o por para aparecer o . Vou de primeira opção porque as curvas de sistema e bombas são com .
Como vimos na teoria, isolamos o e o que sobra é o ; temos essa igualdade no ponto de operação. Daí, rearranjando:
Passo 2
Bora simplificar essa equação!
- “Não há diferença de elevação entre os pontos de captação e descarga da água” Então:
- O enunciado fala que são LAGOAS de aeração. Você já viu alguma lagoa que não seja aberta pra atmosfera? Haha Daí, pegando pontos 1 e 2 no topo das superfícies de líquido:
- Uma lagoa é imensa comparada à uma tubulação de de diâmetro, concorda? O líquido que sai e entra nessas lagoas é coisa pouca perto do líquido que tem nas lagoas então a altura de líquido praticamente não se move.
Com isso:
Quanto ao , sabemos que ele tem duas contribuições:
Em que:
O enunciado diz que não tem acidentes então . Quanto à , podemos, lá de Mecânica dos Fluidos, escrevê-lo em função do fator de atrito de Moody:
Em que é a velocidade média dentro na tubulação. Daí:
E temos a expressão de em função de . Mas ainda precisamos dar mais uma trabalhada nisso.
Passo 3
Chegamos em:
Substituindo a expressão de em função de :
E podemos colocar esse em função da vazão também.
O enunciado deu que o diâmetro é . Repara que tá tudo em metro então tenho que usar o diâmetro em metro também. Calculando a área transversal:
Nesses concursos geralmente não pode usar calculadora, então eles simplificam as coisas falando pra usar .
Daí:
Temos também que , e :
Resolvendo essa equação, achamos a vazão de operação, mas nem precisamos resolver; o enunciado pediu a equação só.
Resposta
Letra d)
Exercício Resolvido #5
UFRJ – Apostila de Mecânica dos Fluidos, Prof. Heloísa
Uma bomba centrífuga é instalada em um sistema de tubulações com comprimento e diâmetro , feitas de ferro fundido. A superfície do reservatório a jusante (após) a bomba está abaixo do reservatório a montante da bomba (antes). Determine a curva do sistema. Estime a potência necessária para que a bomba funcione à vazão de . Os reservatórios estão abertos para a atmosfera.
Passo 1
O enunciado descreve uma instalação e pede primeiro pra determinar a curva do sistema. Precisamos, então, lembrar quem é o , lá da teoria. Partindo do balanço de energia dividido por , é só isolar o e todo o resto é . O balanço de energia é:
Nesses casos de reservatórios, é conveniente usar a superfície dos reservatórios como esses pontos 1 e 2 a serem analisados. Chamando de:
E isso é conveniente porque o volume de líquido saindo ou entrando em um reservatório é muito pequeno face ao volume que tem nele. Aí podemos aproximar que altura de líquido quase não se move, daí:
Outro ponto importante sobre estes reservatórios é que estão abertos para a atmosfera e como escolhemos pontos na superfície do líquido, isto é, em contato com a atmosfera:
Substituindo isso tudo no balanço de energia:
Dividindo por e isolando o :
Podemos, ainda, abrir esse termo de perda de carga total:
Em que:
Como o enunciado não fala nada de acidentes (exemplo: válvulas, curvas etc), só tem esse termo . E podemos escrevê-lo em termos do fator de atrito de Moody :
Em que esse é a velocidade média dentro da tubulação.
Substituindo no balanço de energia:
Em que o termo em vermelho é o .
Substituindo os valores dados no enunciado
Como é função de , o valor de varia conforme a varia (ou ; dá no mesmo). Daí, vamos ter que estimar para cada vazão analisada; para isso, pode-se usar ou a correlação de Colebrook ou o diagrama de Moody. Vou usar a segunda opção.
Passo 2
Para construir a curva do sistema, precisamos do valor de para diferentes valores de vazão . Vou construir uma tabela pra organizar a obtenção desses pontos, ok? E vou usar nos cálculos, para a água:
Também vamos precisar da rugosidade do ferro fundido para ver os valores no diagrama de Moody. Procurando na literatura:
Daí:
Aí, variando valores de vazão:
Plotando valores de , obtemos a curva do sistema:
E quero destacar uma coisa pra você: esses pontos em que deu negativo significa que não precisaria de bomba nesses casos; só a diferença de altura já daria conta do transporte do líquido de um ponto a outro. Lembre que a definição de é quanto de carga o sistema precisa naquelas condições.
Passo 3
Por fim, é pedido pra calcular a potência da bomba que opere à vazão de .
“Ah, mas eu não lembro a fórmula de potência”! Então bora pelas unidades. Uma unidade de potência é . Temos que a unidade de está em . Daí, dá pra chegar em:
Alternativamente:
Agora é só lembrar que no ponto de operação:
E com nós já calculamos está na tabela. Daí:
Resposta
Exercício Resolvido #6
UFPE – Cálculo 1 – Listas de Cálculo 1 – 1ª Lista – 2022.2 – Exercício 1a
Calcule os seguintes limites:
Passo 1
Fala aí galera, bora resolver o nosso exercício?
Vamos substituir o valor que está tendendo:
Show, nos vemos no próximo exercício.
Resposta
Exercício Resolvido #7
UFPE – Cálculo 1 – Listas de Cálculo 1 – 1ª Lista – 2022.2 – Exercício 1a
Calcule os seguintes limites:
Passo 1
Fala aí galera, bora resolver o nosso exercício?
Vamos substituir o valor que está tendendo:
Show, nos vemos no próximo exercício.
Resposta
Exercício Resolvido #8
UFPE – Cálculo 1 – Listas de Cálculo 1 – 1ª Lista – 2022.2 – Exercício 1a
Calcule os seguintes limites:
Passo 1
Fala aí galera, bora resolver o nosso exercício?
Vamos substituir o valor que está tendendo:
Show, nos vemos no próximo exercício.
Resposta
Exercício Resolvido #9
Passo 1
Para resolver essa integral, podemos usar a substituição trigonométrica. Neste caso, vamos usar a identidade trigonométrica para simplificar a integral.
Começamos com a integral original:
Usando a identidade , podemos reescrever como
Passo 2
Passo 3
Resposta
Exercício Resolvido #10
Passo 1
Para resolver essa integral, podemos usar a substituição trigonométrica. Neste caso, vamos usar a identidade trigonométrica para simplificar a integral.
Começamos com a integral original:
Usando a identidade , podemos reescrever como