Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 6.3 - Ex. 29

Uma clínica de emagrecimento recebe pacientes aldultos com peso seguindo uma distribuição normal de média 130 k g e desvio padrão 20 k g . Para efeito de determinar o tratamento mais adequado, os 25 % pacientes de menor peso são classificados de “magros”, enquanto os 25 % de maior peso de “obesos”.

Determine os valores que delimitam cada uma dessas classificações.

Passo 1

Definindo nossa variável como,

X = p e s o   d o s   p a c i e n t e s   ( e m   k g )

De forma que:

X ~ N 130 ; 20 2

Vamos então, usar a aproximação pela normal padrão, teremos o seguinte:

Z = X - μ σ ~ N ( 0,1 )

E lembrando que, seja a probabilidade:

P a ≤ X ≤ b = P a - μ σ ≤ Z ≤ b - μ σ

Passo 2

Agora, perceba que o enunciado pede um valor t , tal que:

P X < t = 0,25

Aplicando aproximação pela normal:

P Z < t - 130 20 = 0,25

Vamos buscar na tabela um valor - z , onde:

- z = t - 130 20

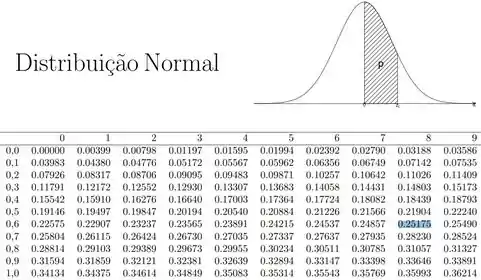
Perceba que:

t - 130 20 = - 0,68

Isolando t :

t = 116,4

Isso significa que:

P X < 116,4 = P Z < - 0,68 = 0,25

Passo 3

Na outra parte da resposta, queremos:

P X > t = 0 , 25

P X > t = P Z > t - 130 20 ⏟ z = 0 , 2 5

Então:

P 0 ≤ Z < + ∞ ⏟ 0,5 - P 0 < Z < z   = 0,25

Ou seja,

P 0 ≤ Z ≤ z = 0,25

Como na primeira perte da resposta, z = 0,68

t - 130 20 = 0,68

Isolando t

t = 143,6 k g

Resposta

Portanto, concluímos que os pacientes com menos de 116,4 k g são classificados como magros; e os com mais de 143,6 k g são colocados no grupo dos obesos.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A quantidade de querosene, em milhares de litros,em um tanque no começo de um dia é a quantidadevariável K, da qual uma quantidade variável X é vendidanaquele dia. Assuma que a função de densidade con
A velocidade de uma molécula em um gás uniformeem equilíbrio é a variável aleatória V, cuja distribuiçãode probabilidade é dada porf ( \ {kv 2e-h"\ v 0,f{v ) = \ 0; contrario,onde k é uma constante ap
Considere X uma variável aleatória binomial comdistribuição de probabilidade/ M . Í Q ( f * - 0 . 1 . 2. 3.10 , caso contrario.Determine a distribuição de probabilidade da variávelaleatória Y - X 2
A função geradora de momento de uma variávelaleatória de Poisson X é dada porMx (t) = e ^ x\Determine P(fi - 2 a
Uma variável aleatória X tem distribuição uniforme discreta/ (*x —1 , 2,..., kycaso contrário.Mostre que a função geradora de momentos de X é'(!- e kt)Mx(t) =k{\ - e‘)