Partindo do repouso quando , a polia tem aceleração , onde é dado em radianos. Determine a velocidade do bloco quando ele atinge a posiç��o . A polia tem um cubo interno que está fixo em e gira com ela.
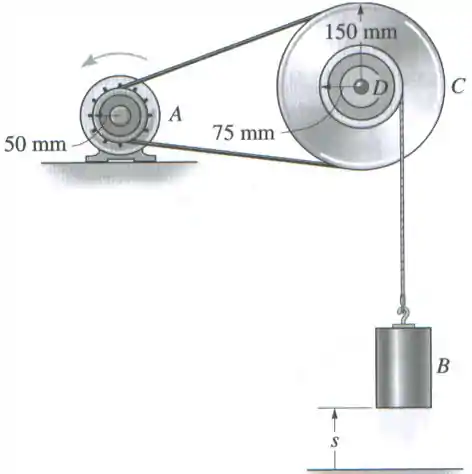
Passo 1
Quando temos duas polias ligadas por uma corda, nós vimos que o tanto que a corda andar na polia é o mesmo tanto que ela vai andar na polia . Ou seja, o deslocamento da corda tanto na polia quanto na polia deve ser o mesmo:
Repare que o bloco está ligado a polia por uma corda, então quando a polia começar a girar vai levantar o bloco . E seguindo o mesmo raciocínio de antes, conforme a polia girar ela vai enrolar a corda em torno de si. Vamos fazer um esqueminha para entendermos melhor.
Na situação inicial, quando , temos:
Quando as polias começarem a girar vamos ter:
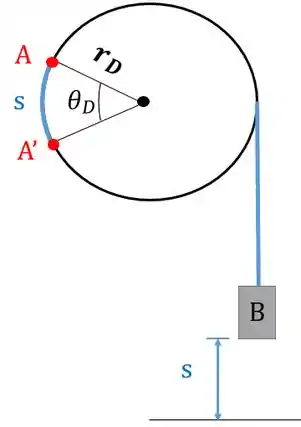
Escrevendo isso matematicamente, temos:
Mas repare que a polia D está fixa na polia C e gira com ela, de modo que:
Vamos substituir isso na equação de
Agora, vamos isolar o nas duas equações que temos até agora que são:
E:
Isolando , vamos ter:
E:
Igualando essas equações, teremos:
Vamos isolar , porque no enunciado foi dada a aceleração da polia :
Passo 2
Vamos pensar em outra relação entre as duas polias. Lembre que a velocidade da corda é sempre a mesma esteja ela passando pela polia ou pela polia , então:
Mas o que queremos saber é a velocidade do bloco B, não é mesmo?
Para calcular a velocidade angular , usamos a seguinte equação:
Mas lembra que a polia e a polia estão girando juntas? Desse modo que . Então, essas duas polias têm a mesma variação do ângulo em relação ao tempo, portanto vão ter a mesma velocidade angular:
Podemos dizer, então que:
Agora, vamos substituir na seguinte equação:
Passo 3
Até agora temos duas equações:
E:
Temos que arranjar um jeito dessas duas equações virar uma só. Vamos achar as variáveis que se repetem nas duas equações: e . Vamos isolar essas variáveis em ambas as equações:
E:
Vamos igualar as equações e isolar o que queremos saber que é o :
Simplificando, temos:
Passo 4
Agora temos que dar um jeito de achar uma relação entre a velocidade angular e a deslocamento angular da polia . Qual é a equação que relaciona essas duas variáveis?
Opa, vamos ter que integrar o lado esquerdo com relação a e o lado direito com relação a :
Lembrando que o enunciado disse que . Vamos colocar isso na nossa integral:
Sabemos que o sistema partiu do repouso então e . Vamos ter que:
Vamos substituir nesta equação aqui:
Simplificando vamos ter:
Então, quando s = 6 m, a velocidade do bloco B será: