Ache a inversa de Laplace da seguinte equação:
Passo 1
Falaaa... beleza???? Vamos fazer essa inversa aqui juntos?? Então bora...
A primeira coisa que vamos fazer é dividir em frações parciais, que vai ficar assim: (repara bem quando o polinômio embaixo é de segundo grau, em cima vai ter um do primeiro grau...)
E vamos usar a tabela de transformadas:
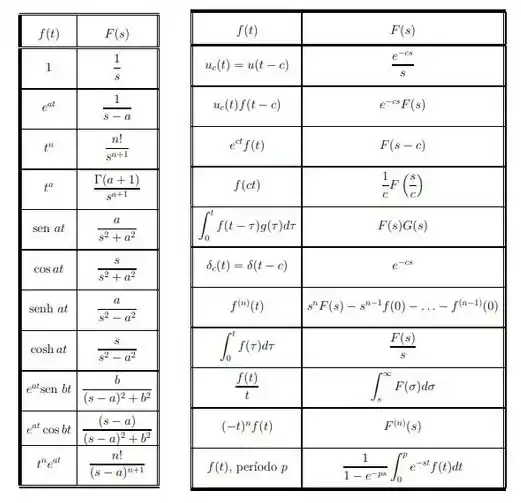
E vamos fazer uma pré seleção das que parecem mais com as do nosso problema:
Passo 2
Vamos achar os , então:
E ficamos com o sisteminha: (igualando o que ta na frente do de um lado e do outro, do e os que não têm )
E achamos:
Então ficamos com:
A gente vai precisar achar a inversa de e de .
Pra é só ver:
Então:
Passo 3
E pra outra vamos precisar fazer algumas manipulaçõezinhas...
Primeiro a gente quer deixar parecido com:
(a gente sempre começa com o “s”, que a do cosseno, porque depois é só ir adicinando alguma coisa e vai dar a do seno)
A gente pode reescrever assim, oh:
E dá pra dividir em duas, ainda:
Passo 4
Vamos pegar a primeira parcela da soma:
Repara que temos o caso e , então vamos ter:
Já pra segunda parcela:
Agora vamos relacionar com o seno:
Entãããooo agora é só somar tudo (ou diminuir porque tem um sinal de menos... só ter atenção):
E acabamos... dá um trabalhinho, mas a gente chega, viu?