O circuito abaixo está operando no estado permanente para , com a chave aberta. Se a chave se fecha em , determine para .
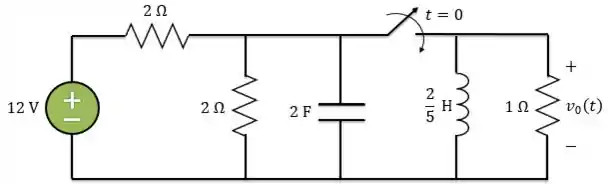
Passo 1
Antes de mais nada, vamos determinar as condições iniciais.
Em , o enunciado disse que o circuito estava em seu regime permanente. Então, podemos considerar o indutor um curto-circuito, o capacitor um circuito aberto e temos o circuito abaixo:
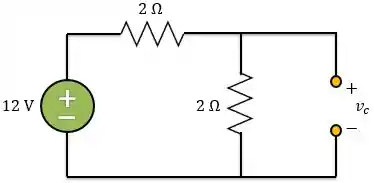
Aplicando divisor de tensão, temos que a tensão no capacitor é
Além disso, como a chave está aberta, não há circulação de corrente pelo indutor.
Em a chave é fechada e temos o seguinte circuito:
Como a tensão no capacitor não pode variar instantaneamente, assim como a corrente no indutor, temos que
Logo,
Passo 2
Agora, vamos encontrar a EDO que descreve no circuito para Então, após o fechamento da chave, a gente tem o circuito abaixo:
Aplicando LCK ao nó do circuito acima,
Dando aquela simplificada,
Passo 3
Aplicando Transformada de Laplace na expressão acima, temos
Substituindo a condição inicial que encontramos:
Temos,
Simplificando,
Isolando a transformada da tensão,
Passo 4
Agora que encontramos a expressão para , vamos utilizar o método de expansão em frações parciais.
Fatorando o polinômio do denominador, temos
Expandindo em frações parciais,
Agora, precisamos determinar as constantes e .
Para temos
Simplificando,
Vamos seguir o mesmo processo para encontrarmos .
Simplificando,
Substituindo o valor de cada constante, temos que
Passo 5
Agora que encontramos a expressão para em frações parciais, vamos aplicar a Transformada inversa de Laplace:
Poderíamos deixar com essa expressão, mas a gente sempre evita grandezas complexas na resposta final. Então, vamos simplificá-la bastante e deixá-la mais bonita.
Lembrando da identidade
Temos,
Portanto,