Determine se o circuito abaixo não contiver energia armazenada para , e se
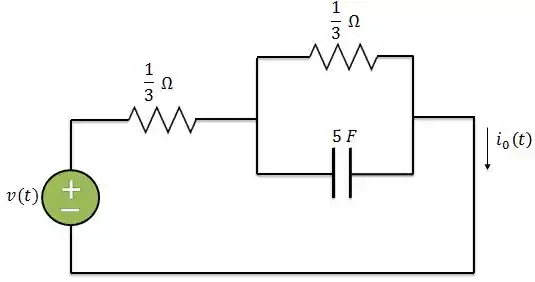
Passo 1
Primeiro, vamos analisar em . Como o impulso de tensão não pode ser aplicado no capacitor nem no resistor que está em paralelo com ele, porque causaria uma mudança repentina na tensão do capacitor.
Ele deve ser aplicado no primeiro resistor de , gerando um impulso de corrente:
Pronto, encontramos a corrente em .
Passo 2
Agora falta calcularmos para
Vamos distribuir a corrente como no circuito abaixo:
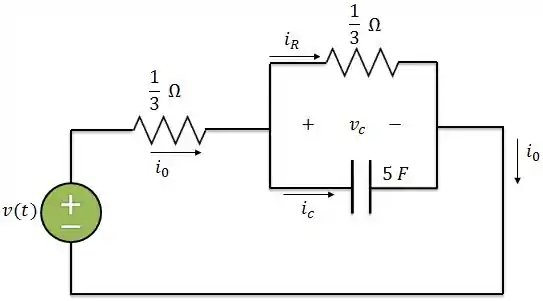
Aplicando a LCK, temos:
Como,
e
Substituindo:
Então, para encontrarmos para , precisamos encontrar antes para podermos substituir na equação aí de cima.
Passo 3
Agora, vamos aplicar a LTK no circuito:
Igualando as duas equações de a gente encontra:
Como,
Temos,
Passo 4
Aplicando Transformada de Laplace na expressão acima, temos
Como estamos resolvendo a EDO por transformada de Laplace, não precisamos considerar como o impulso afeta as condições iniciais da tensão do capacitor. Pois quando fazemos a transformada do impulso essa condição já está presente nela.
Logo, como capacitor estava inicialmente descarregado,
Lembrando que a tensão no capacitor não pode variar instantaneamente, então:
Logo,
Isolando a transformada da tensão,
Passo 5
Aplicando a Transformada inversa de Laplace:
Logo,
Passo 6
Agora que encontramos , podemos substituí-lo na equação abaixo para encontrarmos para
Simplificando:
Portanto:
Que também podemos escrever assim: