Lei da Refração
Produzido por Bruno SoaresTeoria
Já tentou falar dentro da água?
Quando você e outra pessoa tentam conversar por baixo d’água, a voz sai estranha, meio grossa, e não conseguimos entender nada!
Isso acontece porque o som atravessa a água com uma velocidade diferente da velocidade que ele atravessa o ar.
Com a luz acontece a mesma coisa.
Quando temos luz atravessando a água, ou um vidro, um plástico, ou qualquer outra coisa, a velocidade dela muda! Por exemplo, a luz no vácuo tem uma velocidade MUITO maior que a luz na água!

Neste tópico, vamos discutir essa mudança de velocidade a partir de uma propriedade bem comum dos materiais.
Entra em cena o índice de refração!
Existe uma grandeza que tem dentro de si a informação da velocidade da luz em um dado meio: o índice de refração. Ele é dado por:
Onde é a velocidade da luz no vácuo, que vale aproximadamente , e é a velocidade da luz no interior do material.
Ou seja, o índice mede a diminuição da velocidade das ondas eletromagnéticas quando elas se propagam em um lugar que não seja o vácuo.
Vale notar três coisas:
- Como o índice de refração é uma razão de velocidades, ele não tem unidade.
- Quanto maior a velocidade no meio, menor o índice de refração.
- Quanto menor a velocidade no meio, maior o índice de refração.
No vácuo, , e por isso .
Agora, embora a velocidade da luz varie de um meio para outro, a sua frequência permanece constante.
Além disso, a velocidade da onda , a frequência e o comprimento de onda estão relacionados por
Então se a velocidade muda e a frequência não, o comprimento de onda tem que mudar também!
Se substituirmos essa equação na fórmula do índice de refração, nós podemos encontrar uma relação entre o comprimento de onda da luz no vácuo e do comprimento de onda no material .
A diferença na imagem observada dentro e fora d’água
Você já viu o mistério do canudo quebrado?

Quando vemos a parte do canudo que fica fora da água e a parte dentro, ele parece meio... bizarro.
Por que isso acontece?
Isso é uma consequência direta da mudança de velocidade da luz: trata-se da refração.
A refração é a mudança da direção de propagação dos raios luminosos que ocorre quando a luz que se propagava em um meio (como o ar) passa a se propagar em outro (como a água).
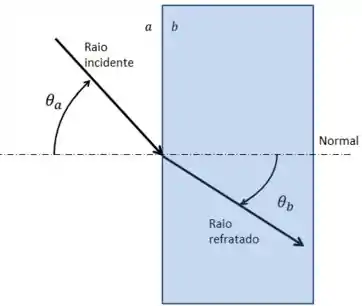
Lei de Snell
A relação entre os ângulos (ângulo de incidência) e (ângulo de refração) é dada pela seguinte fórmula:
Que é conhecida como Lei de Snell.
Nessa fórmula, temos que é o índice de refração do meio e é o índice de refração do meio . Ela nos diz o seguinte:
- Se , então ( Quando a luz refrata de um meio com maior índice de refração para um com menor índice, o ângulo de refração é maior que o ângulo de incidência)
- Se , então ( Quando a luz refrata de um meio com menor índice de refração para um com maior índice, o ângulo de refração é menor que o ângulo de incidência)
Contudo, ela tem uma limitação:
Ambos os ângulos de incidência e de refração devem ser menores de . Esse é um ângulo limite pois nos casos em que os ângulos seriam “maiores” o que acontece é que na verdade não teremos refração!
Análise Gráfica da Refração
Se tem uma coisa que vira e mexe aparece em questões de prova ou de lista de exercícios, essa coisa é “gráficos”.
Por isso, este tipo é destinado a observamos os gráficos que podem aparecer na sua vida.
O ângulo de refração é sempre dado pela Lei de Snell (considerando ângulos menores que )
Podemos rearrumá-lo e ver que:
Ou, pra quem preferir, podemos já inverter:
Essas fórmulas nos dizem o seguinte:
- O ângulo de refração depende do ângulo de incidência . Quanto maior o ângulo de incidência, maior o ângulo de refração.
- O ângulo de refração depende do inverso do índice de refração , do meio onde a luz refrata. Quanto maior esse índice, menor o ângulo que a luz faz com a reta normal à interface.
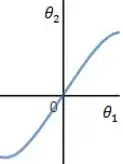
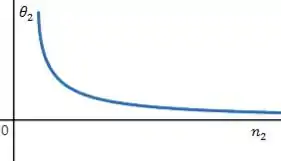
Em geral, os gráficos vão nos dar pares de valores de e ou pares de valores de e .
Então, a questão pode te dar uma terceira informação (ou o ângulo que falta ou um dos índices de refração) e te pedir pra encontrar o que falta.
Agora vamos praticar em alguns exercícios?
Entra em cena o índice de refração!
A diferença na imagem observada dentro e fora d’água
Lei de Snell
Análise Gráfica da Refração
Exercícios Resolvidos
Exercício Resolvido #1
Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, pp 29-33.5
Um feixe de luz desloca-se no quartzo com velocidade . O comprimento de onda da luz no quartzo é .
- Qual é o índice de refração do quartzo para esse comprimento de onda?
- Se essa mesma luz se propagasse no ar, qual seria seu comprimento de onda?
Passo 1
Letra a)
O problema nos dá a velocidade da luz no quartzo e o comprimento de onda no quartzo .
A letra a) nos pede o índice de refração do quartzo.
Quando falamos sobre o índice de refração, vimos que ele pode ser calculado através do comprimento de onda e da velocidade , através das seguintes relações:
Onde é a velocidade da luz no vácuo, que vale e é o comprimento de onda no vácuo.
Passo 2
Como já sabemos o valor de e o valor de que é preestabelecido, vamos usar a relação:
Onde:
;
;
Logo:
Passo 3
Letra b)
A letra b) nos pede para calcular o comprimento da onda caso ela se propagasse no ar.
Antes de começar a resolver a questão, é importante lembrar uma informação muito importante:
Como o índice de refração no ar é aproximadamente igual ao do vácuo, usaremos e para a velocidade de onda no ar e o comprimento de onda no ar, respectivamente.
Beleza?! Ok, então vamos continuar.
Conforme falamos anteriormente, o índice de refração pode ser calculado por:
Onde é o índice de refração no quartzo (que calculamos na letra a)), e o comprimento de onda no ar e é o comprimento de onda no quartzo.
Passo 4
Onde:
;
;
Logo:
Resposta
Letra a)
Letra b)
Exercício Resolvido #2
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 100-4
O comprimento de onda da luz amarela do sódio no ar é .
- Qual é a frequência da luz?
- Qual é o comprimento de onda da luz em um vidro com um índice de refração de ?
- Use os resultados dos itens (a) e (b) para calcular a velocidade da luz no vidro.
Passo 1
Letra a)
A velocidade da luz no ar é constante e igual a e ela é dada por:
Sendo que o comprimento da luz amarela do sódio é:
Logo, sua frequência vai ser:
Passo 2
Letra b)
Quando a luz passa do ar pro vidro, seu novo comprimento de onda vai ser dado por:
Onde é o comprimento da luz no ar. Assim:
Passo 3
Letra c)
A velocidade da luz no vidro vai ser:
Resposta
Letra a)
Letra b)
Letra c)
Exercício Resolvido #3
Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, pp 29-33.15
Um raio de luz incide sobre a superfície plana que separa duas placas finas de vidro com índices de refração e .
O ângulo de incidência é , e o raio que provém da placa que possui índice de refração .
Calcule o ângulo de refração.
Passo 1
O problema nos dá os índices de refração e e o ângulo de incidência .
A questão nos pede para calcular o ângulo de refração
A equação que melhor se encaixa para resolver o problema é a Lei de Snell, dada por:
Passo 2
Onde:
;
;
;
Logo:
Resposta
Exercício Resolvido #4
Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, pp 29-33.9
Um raio de luz que se propaga no ar incide sobre a superfície de um bloco de plástico em um ângulo de com a normal e se desvia até formar um ângulo de com a normal no plástico.
Calcule a velocidade da luz no plástico.
Passo 1
O problema nos dá o ângulo de incidência e o ângulo de refração .
Sabemos que o índice de refração no ar é aproximadamente igual a .
O problema nos pede para calcular a velocidade da luz no plástico . Para isso, é preciso descobrir o índice de refração no plástico, já que:
Com os dados que o problema nos dá, a melhor maneira de encontrar o valor de é através da Lei de Snell, dada por:
Passo 2
Onde:
;
;
;
;
;
Logo:
Passo 3
Onde:
;
;
Logo:
Resposta
Exercício Resolvido #5
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 100-3
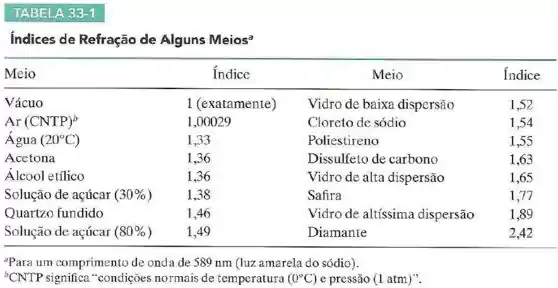
Qual é a diferença, em metros por segundo, entre a velocidade da luz na safira e a velocidade da luz no diamante?
Veja a Tabela 33-1.
Passo 1
A velocidade da luz no vácuo é de aproximadamente .
De forma mais exata:
Quando a luz se propaga em algum outro meio que não o vácuo, a sua velocidade diminui de forma que:
Onde é o índice de refração do meio.
Passo 2
Para a safira , e a velocidade da luz fica:
Para o diamante , e a velocidade da luz fica:
Assim, a diferença entre as velocidades é:
Resposta
Exercício Resolvido #6
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 99-2
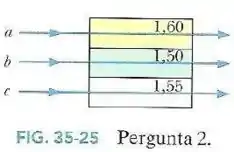
Na Fig.35-25 três pulsos luminosos de mesmo comprimento de onda, , e , atravessam blocos de plásticos de mesmo comprimento cujos índices de refração são dados.
Coloque os pulsos na ordem do tempo que levam para atravessar os blocos, começando pelo mais lento.
Passo 1
O índice de refração de um meio é definido como a razão entre a velocidade da luz no vácuo (ou no ar, que são muito parecidas) e a velocidade da luz no meio.
Em outras palavras:
Então quanto menor a velocidade da luz no meio, maior o índice de refração daquele meio. Dito de outra forma:
Vamos inverter o que dissemos:
Quanto maior o índice de refração, menor a velocidade da luz.
Passo 2
Imagina um carro.
Sabemos que, quanto maior a velocidade do carro, menor o tempo que ele demora pra percorrer um certo comprimento.
No nosso caso, para a luz, essa velocidade depende do índice de refração.
Vamos ter que:
Maior índice de refração Menor velocidade Maior tempo gasto
Logo, quanto maior o índice de refração, maior o tempo gasto.
Colocando os pulsos na ordem crescente de tempo que gastam para atravessar os blocos:
Resposta
Exercício Resolvido #7
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 101-8
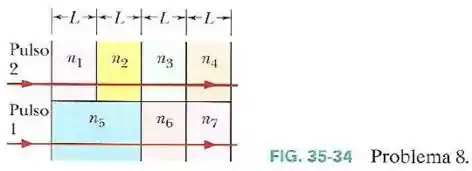
Na Fig.35-34, dois pulsos luminosos atravessam placas de plástico de espessura ou e índices de refração , , , , , e .
- Qual dos dois pulsos chega primeiro à outra extremidade das placas?
- A diferença entre os tempos de trânsito dos dois pulsos é igual a que múltiplo de ?
Passo 1
Letra a)
Digamos que um pulso de luz tem uma velocidade ao atravessar uma placa com índice de refração . Essa velocidade vai ser:
O tempo que esse pulso vai levar para atravessar uma placa com largura vai ser:
Passo 2
O tempo que o pulso dois leva para atravessar o bloco todo vai ser a soma dos tempos em cada placa.
Pelo enunciado:
Já o tempo que o pulso um vai levar vai ser:
Pelo enunciado:
O que nos mostra que o pulso dois chega primeiro à outra extremidade das placas.
Passo 3
Letra b)
A diferença entre os tempos de trânsito é:
Resposta
Letra a)
O pulso dois atinge a outra extremidade das placas primeiro.
Letra b)
A diferença entre os tempos de trânsito dos dois pulsos é de .
Exercício Resolvido #8
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 32-46
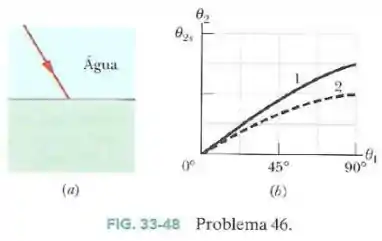
Na Fig.33-48a um raio luminoso que está se propagando inicialmente na água incide com um ângulo em outro material, no qual parte da luz se refrata. O outro material pode ser do tipo ou do tipo ; a Fig.33-48b mostra o ângulo de refração em função do ângulo de incidência para os dois tipos de material.
A escala do eixo vertical é definida por . Sem fazer nenhum cálculo, determine:
- Se o índice de refração do material é maior ou menor que o índice de refração da água ()
- Se o índice de refração do material é maior ou menor que o índice de refração da água.
- Do material .
- Do material .
Determine o índice de refração:
Passo 1
Letra a)
Seja o índice de refração da água e o índice de refração do material.
- O ângulo de refração é maior que o ângulo de incidência somente se .
- O ângulo de refração é menor que o ângulo de incidência somente se .
No caso da curva do material , é difícil confirmar graficamente para ângulos muito pequenos, mas para acima de fica mais claro que o ângulo de refração é menor que o ângulo de incidência.
Passo 2
Letra b)
Usando o mesmo raciocínio do item anterior, mas agora com a curva do material .
Neste caso, é mais fácil observar até mesmo para ângulos pequenos que o ângulo de refração é menor que o ângulo de incidência.
Passo 3
Letra c)
Para calcular o índice de refração, precisamos de algum ponto onde seja claro qual o ângulo de refração.
Podemos observar que quando teremos . ( Como , a unidade do eixo vertical é ).
Substituindo na lei de Snell:
Passo 4
Letra d)
O mesmo procedimento do item pode ser feito aqui, inclusive usando também para o qual .
Resposta
Letra a)
Letra b)
Letra c)
Letra d)
Exercício Resolvido #9
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 32-48
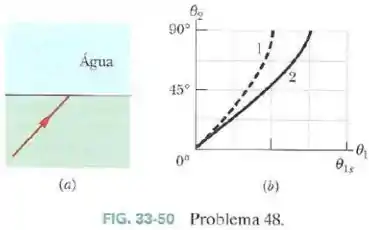
Na Fig.33-50a um raio luminoso que está se propagando inicialmente em um certo material incide com um ângulo na água, onde parte da luz se refrata. O outro material pode ser do tipo ou do tipo ; a FIg.33-50b mostra o ângulo de refração em função do ângulo de incidência para os dois tipos de material.
A escala do eixo horizontal é definida por . Sem fazer nenhum cálculo, determine:
- Se o índice de refração do material é maior ou menor que o índice de refração da água ().
- Se o índice de refração do material é maior ou menor que o índice de refração da água.
- Do material .
- Do material .
Determine o índice de refração:
Passo 1
Letra a)
Seja o índice de refração da água e o índice de refração do material.
- O ângulo de refração é menor que o ângulo de incidência somente se .
- O ângulo de refração é maior que o ângulo de incidência somente se .
Lembrando que a luz está refratando na água.
Como o ângulo de refração é sempre maior que o ângulo de incidência para a curva 1:
Passo 2
Letra b)
Semelhante ao caso da letra , o ângulo de refração da curva é sempre maior que o ângulo de incidência. Isso nos diz que:
Passo 3
Letra c)
A unidade do eixo horizontal do gráfico é de , ou seja, .
Assim, olhando a curva para , teremos
Passo 4
Letra d)
Olhando a curva , para teremos .
Resposta
Letra a)
Letra b)
Letra c)
Letra d)
Exercício Resolvido #10
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 32-50
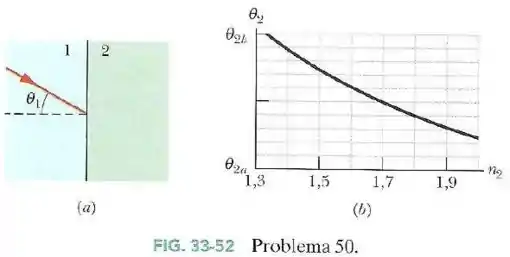
Na Fig.33-52a um feixe luminoso que está se propagando inicialmente no material incide no material com um ângulo de . A refração da luz no material depende, entre outros fatores, do índice de refração do material .
A Fig.33-52b mostra o ângulo de refração em função de . A escala do eixo vertical é definida por e .
- Qual é o índice de refração do material ?
- Se o ângulo de incidência aumenta para e , qual é o valor de ?
Passo 1
Letra a)
A dependência do ângulo de refração com o índice de refração do meio é dada pela Lei de Snell:
Nós temos o ângulo de incidência . Agora, precisamos de algum ponto no gráfico que nos dê e , para podermos substituir e achar .
Um ponto no gráfico que vai facilitar o nosso trabalho é o correspondente a , pois para este ponto o ângulo dado pela escala do eixo vertical é .
(no eixo vertical, os limites são e , e o nosso ponto é exatamente o ponto médio, logo ).
Ficamos com:
Passo 2
Letra b)
Graças ao gráfico, nós já temos o índice de refração . Com posse dos valores de e , podemos substituí-los na Lei de Snell:
Resposta
Letra a)
Letra b)
Exercício Resolvido #11
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 100-2
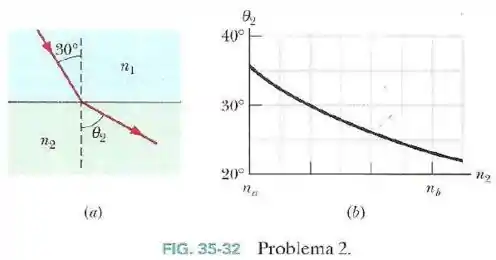
Na Fig.35-32a, um raio luminoso que estava se propagando no material incide em uma interface com um ângulo de . O desvio sofrido pelo raio devido à refração depende, em parte, do índice de refração do material .
A Fig.35-32b mostra o ângulo de refração em função de . A escala do eixo horizontal é definida por e .
Qual é a velocidade da luz no material ?
Passo 1
Para sabermos a velocidade da luz no material precisamos primeiro conhecer o índice de refração . Vamos usar o gráfico para encontra-lo.
A dependência do ângulo de refração com o índice de refração é dada pela lei de Snell:
Sabemos o ângulo de incidência . O ponto no gráfico correspondente a vai ser aquele onde .
Passo 2
Pela escala do eixo horizontal, cada unidade (traço mais escuro) é dada por:
(pois entre e temos três unidades)
Sendo o ângulo de corresponde à uma unidade depois de , temos que .
Pelo que falamos antes, teremos;
Passo 3
O índice de refração de um material é definido como:
Onde é a velocidade da luz no material, é a velocidade da luz no vácuo e é o índice de refração do material .
Resposta
Exercício Resolvido #12
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 32-51, modificado
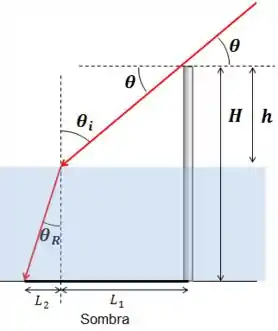
Na Fig.33-53 uma estaca vertical com de comprimento se projeta do fundo de uma piscina até um ponto acima da água. O sol está acima do horizonte.
Qual é o comprimento da sombra da estaca no fundo da piscina?
O índice de refração da água é de .

Passo 1
Primeiro, o ideal é tentarmos montar a geometria do problema, para não nos perdermos no nosso objetivo.
A sombra da estaca vai ser projetada por um raio que passa no topo dela, bate na superfície da água e, por causa da Lei de Snell, tem sua direção alterada ao entrar na água, e forma uma sombra no fundo da piscina.
Passo 2
Agora que já montamos o problema em um desenho (bem bonito, por sinal, e fui eu que fiz =D ) podemos tentar ver o comprimento da sombra.
Vamos de trás pra frente:
Podemos pensar na sombra em duas partes.
Uma parte vai da base da estaca até o comprimento que a luz entra na água. Ela é dada por:
A segunda parte vai ser:
Então, precisamos encontrar os ângulos de incidência e refratado.
Passo 3
Para o ângulo de incidência, note que temos um triângulo retângulo com os ângulos internos e e o enunciado nos diz que . Isso significa que:
Já para o ângulo refratado nós podemos usar a lei de Snell:
Lembrando que o índice do ar é aproximadamente , e o problema nos diz que :
Lembrando que se você precisar transformar ângulos de grau pra radiano e vice versa (caso sua calculadora só tenha um ou outro) você pode usar a regra de três:
Passo 4
Finalmente temos todas as informações necessárias para encontrar o comprimento da sombra.
- Pelo passo anterior, e .
- Pelo enunciado, e .
Logo, além do meu desenho estar extremamente fora de escala, o comprimento da sombra é:
Resposta
O comprimento da sombra é de .
Exercício Resolvido #13
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 106-83
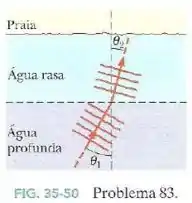
Ondas oceânicas, com uma velocidade de , se aproximam da praia fazendo um ângulo de com a normal, como se vê na vista de topo da Fig.35-50. A profundidade da água muda bruscamente a uma certa distância da praia, fazendo a velocidade das ondas diminuir para .
- Qual é o ângulo entre a direção das ondas e a normal perto da praia? (Suponha que a lei de refração é a mesma que para a luz)
- Explique por que quase sempre as ondas incidem perpendicularmente à praia, mesmo quando se aproximam da costa fazendo um ângulo relativamente grande com a normal.
Passo 1
Letra a)
No caso da água, nós não podemos simplesmente definir um “índice de refração” como a razão da velocidade da luz no vácuo e a velocidade de uma onda de água na água salgada. Isso não faria nenhum sentido! (isso não te impediria de tentar definir mesmo assim, e fazer dar certo, porque daria certo mesmo)
Mas vamos olhar a lei de refração de uma forma um pouco diferente, abrindo a definição do índice de refração:
Ela vai ficar:
Onde cortamos a velocidade da luz no vácuo de um lado e do outro. Dessa forma faz mais sentido sairmos colocando valores para ondas de água invés de ondas eletromagnéticas né?
Passo 2
A onda incidente faz um ângulo e tem uma velocidade de enquanto a onda refratada tem uma velocidade de .
Assim, rearranjando a equação anterior:
Passo 3
Letra b)
O ângulo que a onda da letra (a) faz com a praia é:
Que é “quase perpendicular” (ok, forcei um pouco a barra).
Se olharmos a equação que nos dá o ângulo da onda refratada, e considerarmos que as ondas sempre perdem velocidade ao chegar perto da praia, vemos que:
Ou seja, a onda sempre se aproxima da normal à praia quando ela vai perdendo velocidade devido à profundidade da água.
Se, desde o ponto que ela se forma, até a praia, ela perder a velocidade diversas vezes, o ângulo que ela faz com a normal vai diminuir cada vez mais, até que seja praticamente igual a zero.
Resposta
Letra a)
Letra b)
Quase sempre as ondas incidem perpendicularmente à praia pois a medida que elas vão perdendo velocidade, seu ângulo com a direção normal à praia vai diminuindo até que seja quase igual a zero.
Exercício Resolvido #14
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 33-54
Na Fig.33-56a um feixe de luz que estava se propagando no material incide com um ângulo na interface com o material . Parte da luz penetra no material e parte dessa luz penetra no material ; todas as interfaces são paralelas.
A orientação do feixe no material depende em parte do índice de refração do terceiro material. A Fig.33-56b mostra o ângulo em função de .
A escala do eixo vertical é definida por e .
- É possível calcular o índice de refração do material com base nessas informações? Se a resposta for afirmativa, determine o valor de .
- É possível calcular o índice de refração do material com base nessas informações? Se a resposta for afirmativa, determine o valor de .
- Se e , qual é o valor de ?
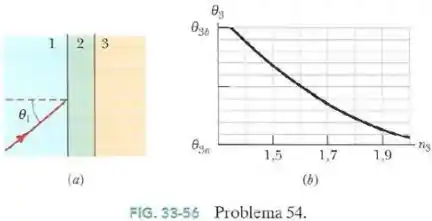
Passo 1
Letra a)
Vamos aos poucos, evitando terrenos perigosos.
O ângulo de refração da luz incidente na interface material -material é dado por:
Porém, pelo fato das interfaces serem paralelas, às retas normais à elas também vão ser paralelas, e o ângulo de refração vai ser o ângulo de incidência na interface material -material .
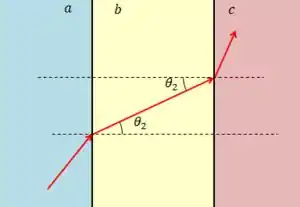
Aplicando a lei de Snell nessa interface:
Como temos e ambos e podem ser obtidos pelo gráfico, é possível encontrar .
Passo 2
O ideal é acharmos o ponto correspondente a no gráfico.
Esse ângulo corresponde à metade do eixo vertical (que varia de a ) e ele corresponde, no eixo horizontal, ao ponto médio entre os índices de refração e , significando que o índice correspondente é .
Passo 3
Letra b)
Poderíamos tentar usar duas fórmulas para calcular . A primeira é:
Mas neste caso, temos (pela letra ) e (pelo enunciado), mas não temos , o que nos impossibilita de achar .
A outra fórmula seria:
Mas nós cairíamos no mesmo problema! Temos vários valores possíveis de e , mas sem não temos como encontrar .
Nós poderíamos tentar usar uma das duas equações para achar e a outra para . Cairíamos no conto do vigário:
Pra achar precisaríamos de e pra achar precisaríamos de !
É um raciocínio circular. Então não temos como encontrar .
Passo 4
Letra c)
Vimos na letra que vale:
Substituindo , e :
Resposta
Letra a)
É possível calcular .
Letra b)
Não é possível calcular .
Letra c)