Obtenção da Série de Fourier
Produzido por Carolina SabaTeoria
Definição
Você já deve ter se deparado com aquelas funções bizarras que dava vontade de chorar! Então a série de Fourier vem para acabar com os nossos problemas. Essa série transforma as funções em soma de senos e cossenos (essas dai a gente gosta!).
Antes de vermos como se transforma uma função na soma de senos e cossenos, vamos entender a fórmula da série de Fourier que é dada por essa expressão:
Calma, vamos explicar o que cada parte significa!
Os termos , e são coeficientes, números, que variam dependendo da função que queremos representar, mais à frente vamos ver como calculá-los, ok?
Esse , presente tanto no seno como no cosseno vem do índice da série, ou seja, fazendo encontramos os termos do somatório.
Como queremos escrever uma função em forma de série, a variável está lá dentro do somatório.
Agora falta esse , o que ele significa? Ele vem do período da função, , que queremos representar.
Fórmula dos coeficientes da série de Fourier
Mas aquela fórmula da Série de Fourier não serve para nada se não tivermos os coeficientes e , não é? Eles são dados pelas seguintes fórmulas:
Mas Atenção!! Veja que fazendo , temos
E cuidado! Na série, o aparece dividido por dois!!
Essas são as fórmulas dos coeficientes da Série de Fourier, grave elas!!
Agora vamos para a parte que interessa: como representar funções por Séries de Fourier? Vamos ver isso na prática!
Exemplo: Esboce o gráfico da função dada e encontre sua Série de Fourier.
Passo 1: Vamos fazer o gráfico de
Para fazer o gráfico de , primeiro nós desenhamos os dados que estão nos colchetes (que valem em ), como fizemos em vermelho. Inclusive os pontos de descontinuidade, as bolinhas cheias e vazias!
Depois, é só repetir esse desenho para a esquerda e para a direita (a cada a função se repete). Inclusive os pontos de descontinuidade, ok?
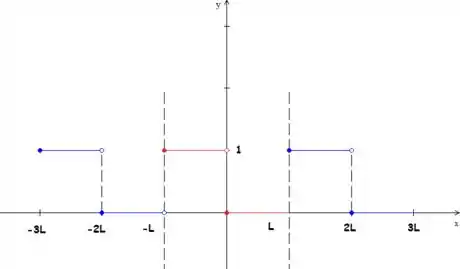
Ponto, essa é a função periódica.
Passo 2: Precisamos agora encontrar a Série de Fourier de , temos o seguinte:
Agora precisamos calcular essas integrais!
Passo 3: Vamos calcular
Fazendo na expressão de , temos:
Ok, mas o que colocamos no lugar de ? Veja no gráfico, que de a temos duas expressões diferentes para , então o único jeito é dividir essa integral em duas, olha só:
Veja os intervalos que escrevemos! A função vale em e em . Resolvendo essas integrais, temos
Passo 4: Agora vamos calcular os outros ’s.
Temos que:
Dividindo essa integral em duas, como fizemos com :
Guarde isso!
Passo 5: Agora só falta calcular os ’s
Dividindo essa integral em duas:
E como:
Sempre que você encontrar um cosseno (ou seno) na expressão do ou tente se livrar dele, porque isso simplifica a resposta. Em das vezes, você consegue fazer isso por essa análise aqui:
Logo
Passo 6: Agora vamos substituir tudo o que encontramos, temos:
Isso nos dá:
Agora vamos com calma. Não podemos escrever direto no somatório porque isso só vale para ímpar! Vamos definir então , porque isso garante que temos índices ímpares, ok? Para temos , portanto a série deve começar em .Temos então
Esses exercícios são realmente trabalhosos, mas a boa notícia é que são todos muito parecidos! Então se você treinar bastante acaba gravando como se faz.
Exercícios Resolvidos
Exercício Resolvido #1
William E. Boyce e Richard C. DiPrima, Equações diferenciais elementares e problemas de contorno, 9ª ed., Rio de Janeiro: LTC, 2010, pp. 314. Exercício 17
a) Esboce o gráfico da função dada por 3 períodos
b) Encontre a série de Fourier da função dada
Passo 1
a)
Para fazer o gráfico de , primeiro nós desenhamos os dados que estão nos colchetes (que valem em ), como fizemos em vermelho.
Depois, é só repetir esse desenho para a esquerda e para a direita (a cada a função se repete).
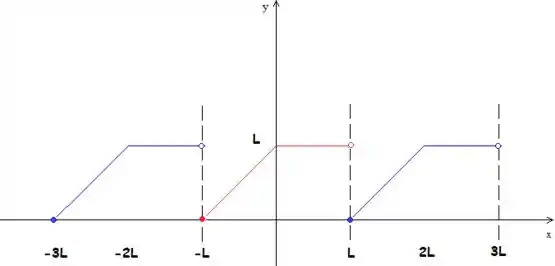
Passo 2
Letra b)
Precisamos agora encontrar a Série de Fourier de , temos o seguinte:
Como , sabemos que o período da função é , esse é o intervalo em que ela se repete. Lembra que a função representada por Série de Fourier tem que ser periódica? Então o da nossa fórmula é o mesmo da função.
Passo 3
Agora vamos calcular
Fazendo na expressão de temos:
Veja no gráfico, que de a temos duas expressões diferentes para , então o único jeito é dividir essa integral em duas, olha só:
Repare nos intervalos que escrevemos! A função vale em e em . Resolvendo essas integrais, temos
Passo 4
Agora vamos calcular os outros ’s. Temos que:
Dividindo essa integral em duas, como fizemos com :
Agora vamos integrar por partes, ok? Fazendo
Como o cosseno é uma função par:
Agora vamos analisar com calma. Perceba que
Logo
Guarde isso!
Obs: sempre que você encontrar um cosseno na expressão do ou do , faça essa análise!
Passo 5
Agora só falta calcular os ’s
Dividindo essa integral em duas:
Agora vamos fazer a integração por partes:
Lembrando que
Temos
Passo 6
Agora vamos substituir tudo o que encontramos, temos:
Vamos separar a série em duas para ver melhor:
Agora vamos com calma. Não podemos escrever direto no somatório porque isso só vale para ímpar. Vamos definir no primeiro somatório, então, , porque isso garante que temos índices ímpares, ok? Para temos , portanto a série deve começar em .Temos então
Agora vamos substituir o valor de usando a notação também, só para ficar igual à primeira série
Já que as duas séries possuem os mesmos índices, podemos juntá-las, não é?
Resposta
Exercício Resolvido #2
William E. Boyce e Richard C. DiPrima, Equações diferenciais elementares e problemas de contorno, 9ª ed., Rio de Janeiro: LTC, 2010, pp. 317. Exercício 6a
Suponha que a função dada é estendida, periodicamente, para fora do intervalo original.
Encontre a série de Fourier da função estendida
Passo 1
Precisamos encontrar a Série de Fourier de , temos o seguinte:
Como o intervalo da função que o problema deu é (de até ) e temos que estender a função, esse será o seu período. Então:
Passo 2
Agora vamos calcular
Fazendo na expressão de temos:
Veja que de a temos duas expressões diferentes para , então o único jeito é dividir essa integral em duas, olha só:
Repare nos intervalos que escrevemos! A função vale em e em . Resolvendo essas integrais, temos
Passo 3
Agora vamos calcular os outros ’s. Temos que:
Dividindo essa integral, como fizemos com :
Agora vamos integrar por partes, ok? Fazendo
Agora temos que integrar por partes de novo ¬¬ , vamos lá
Agora vamos analisar com calma. Perceba que
Logo
Guarde isso!
Passo 4
Agora só falta calcular os ’s
Dividindo essa integral:
Agora vamos fazer a integração por partes:
Agora temos que integrar por partes de novo
Lembrando que
Temos
Você poderia ter separado os ’ s em ’s ímpares e pares também, mas talvez ficasse mais complicado aqui! Vamos deixar assim então.
Passo 5
Agora vamos substituir tudo o que encontramos, temos:
Temos então
Resposta
Exercício Resolvido #3
UFRJ - Cálculo 4 - P2 2012.1 – 1
Seja uma função - periódica , tal que se .
a) Esboce o gráfico de no intervalo .
b) Calcule a série de Fourier da função .
Passo 1
Letra a)
Vamos fazer primeiro o gráfico porque isso facilita muito a questão, ok? Bom, como o enunciado diz que a função é -periódica e nos dá o seu valor no intervalo , sabemos que esse é o período da função.
Vamos então desenhar . Não sabe fazer isso? Primeiro você tem que lembrar que o seno é como se fosse um “S” nessa parte perto da origem. Como fizemos abaixo em vermelho, ok?
Certo, mas queremos o módulo do seno, não o seno. Módulo significa “levar tudo para cima do eixo ”, grave isso. Como assim? A parte da direita já está acima do eixo , então não mexemos nela! A da esquerda, temos que levar para cima, espelhando:
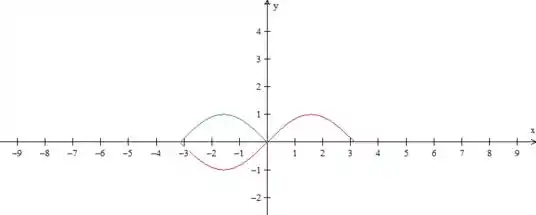
Certo, então a função é representada por esse dois morrinhos aí. Como esse é o período, agora temos que repetir o padrão:
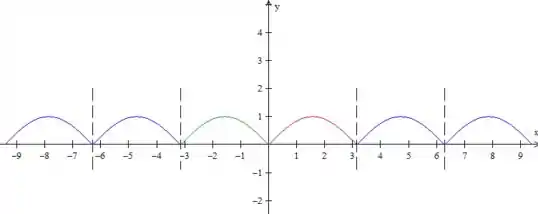
Pronto, essa é a função periódica . Percebeu que ela é uma função especial? Ela é espelhada no eixo , ou seja
Portanto, temos uma função par aqui.
Passo 2
Beleza, agora vamos montar o problema. Como a função é par, temos o seguinte:
Lembra que a função representada por Série de Fourier tem que ser periódica? Então, como o período da função é :
Passo 3
Agora vamos calcular
Fazendo na expressão de e , temos:
Como em , temos:
Logo
Passo 4
Agora vamos calcular os outros ’s. Temos que:
O que nos dá
Beleza, agora temos que ver como integrar isso aqui né. Sempre que você encontrar uma integral de seno vezes um cosseno de números diferentes, pode pensar em aplicar as seguintes fórmulas trigonométricas:
O que nos dá:
Sem isso é meio complicado resolver a integral, então vale à pena memorizar essa fórmula aqui! A integral fica então:
Beleza, agora vamos analisar esses cossenos:
Para e
Para e
Para e
Percebeu então que esses cossenos são o mesmo que ? Vamos escrever isso
Se é ímpar isso aí dá zero, né? Temos isso aqui:
Não percebeu isso na hora? Deixa daquele jeito lá em cima mesmo! Não está errado, essa só é uma forma mais simplificada. Vamos lá então, tá quase acabando.
Passo 5
Agora vamos substituir tudo o que encontramos, temos:
O que nos dá
Deixamos o por último que é mais chatinho.
Não podemos escrever direto no somatório porque isso só vale para par! Vamos definir então , porque isso garante que temos índices pares, ok? Para temos , que é onde a série começa, já que nos ’s ímpares são zero, portanto a nova série deve começar em . Temos então