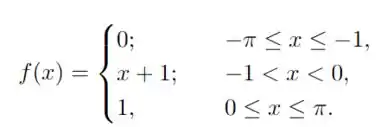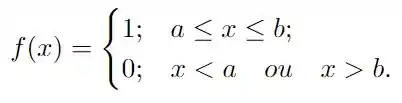Exercícios de Obtenção da Série de Fourier - Lista de Exercícios Resolvida
Questão 1
a) Esboce o gráfico da função dada por 3 períodos
b) Encontre a série de Fourier da função dada
Ver solução completaQuestão 2
Seja uma função - periódica , tal que se .
a) Esboce o gráfico de no intervalo .
b) Calcule a série de Fourier da função .
Ver solução completaQuestão 3
Suponha que a função dada é estendida, periodicamente, para fora do intervalo original.
Encontre a série de Fourier da função estendida
Ver solução completaQuestão 4
Dê a fórmula (sem calcular as integrais resultantes) dos coeficientes que minimizam a expressão:
Ver solução completaQuestão 6
Considere se e tal que .
(a) (2pts) Mostre que a série de Fourier de é dada por
(b) (2pts) Utilizando o item (a) prove que
Ver solução completaQuestão 7
Calcule a expansão em série de Fourier da extensão par de período 4 da função definida no intervalo por :
Escolha uma opção:
a)
b)
c)
d)
e)
Ver solução completaQuestão 8
Considere a função , onde x varia no intervalo Calcular a série de fourier associada a função . O símbolo representa a constante matemática de valor 3,1415926535...
( )
( )
( )
( )
( )
Ver solução completaQuestão 11
Seja a função
Na série de Fourier chega-se a
Podemos afirmar que o valor de é:
( )
( )
( )
( )
( )
Ver solução completaQuestão 14
Dada a função:
- Calcule a soma da série:
Sugestão: integre a série de Fourier de
No intervalo de [0,2]
Ver solução completaQuestão 15
Considere a função periódica de período , que no intervalo é definida por e seja a sua série de Fourier.
- Escreva como deve ser sem calcular coeficientes e , mas apenas escrevendo as integrais que dão seus valores.
- Calcule e ,
- Calcule .
- Calcule .
- Determine os valores de para os quais .
Questão 16
A série de Fourier da função definida por:
Converge em para:
Escolha uma opção:
a)
b)
c)
d) não converge
Ver solução completaQuestão 17
Calcule a série de Fourier em da função :
Escolha uma opção:
a)
b)
c)
d)
e)
Ver solução completaQuestão 18
Determine a série de Fourier da função no intervalo
Escolha uma opção:
a)
b)
c)
d)
e)
Ver solução completaQuestão 19
Determine a série de Fourier da função no intervalo
Escolha uma opção:
a)
b)
c)
d)
e)
Ver solução completaQuestão 20
Seja função contínua, e . Se é a série de Fourier de função qualquer .
Podemos afirmar que:
(I) é sempre zero, para todo
(II) nunca é zero, para todo
Escolha uma opção:
a) As duas afirmações são verdadeiras
b) Somente a afirmação I é verdadeira
c) Somente a afirmação II é verdadeira
d) As duas afirmações são falsas
Ver solução completaQuestão 21
Determine a série de Fourier da função definida por:
No intervalo :
Escolha uma opção:
a)
b)
c)
d)
e)
Ver solução completaQuestão 22
A série de Fourier da função definida por:
Converge em para:
Escolha uma opção:
a)
b)
c) não converge
d)
Ver solução completaQuestão 24
Considere a função definida no intervalo .
Sem calcular os coeficientes, determine o valor da série de Fourier em senos no ponto .
Ver solução completaQuestão 25
Considere a função definida no intervalo .
Calcule os coeficientes da série de Fourier de em cossenos.
Ver solução completaQuestão 26
Esboce o gráfico da função definida por
em que a série do segundo membro é a série de Fourier da função , periódica de período , dada por
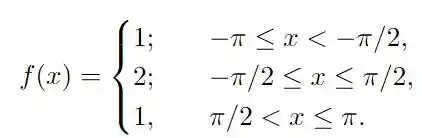
Justifique a construção do seu gráfico.
Ver solução completaQuestão 27
Calcule a série de Fourier das funções a seguir, definidas no intervalo .
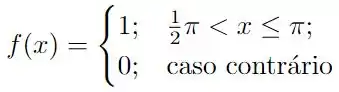
Questão 28
Obtenha a série de Fourier em senos de cada uma das funções a seguir. Você pode utilizar a applet da Sagemath disponibilizada no Moodle. Em cada caso, esboce seu gráfico no intervalo
Ver solução completaQuestão 29
Obtenha a série de Fourier em cossenos de cada uma das funções a seguir. Você pode utilizar a applet da Sagemath disponibilizada no Moodle. Em cada caso, esboce seu gráfico no intervalo
Ver solução completaQuestão 30
Obtenha a série de Fourier em senos de cada uma das funções a seguir. Você pode utilizar a applet da Sagemath disponibilizada no Moodle. Em cada caso, esboce seu gráfico no intervalo
Ver solução completaQuestão 31
Obtenha a série de Fourier em senos de cada uma das funções a seguir. Você pode utilizar a applet da Sagemath disponibilizada no Moodle. Em cada caso, esboce seu gráfico no intervalo
Ver solução completaQuestão 32
Obtenha a série de Fourier em senos de cada uma das funções a seguir. Você pode utilizar a applet da Sagemath disponibilizada no Moodle. Em cada caso, esboce seu gráfico no intervalo
Ver solução completaQuestão 33
Obtenha a série de Fourier em senos de cada uma das funções a seguir. Você pode utilizar a applet da Sagemath disponibilizada no Moodle. Em cada caso, esboce seu gráfico no intervalo
Ver solução completaQuestão 34
Obtenha a série de Fourier em senos de cada uma das funções a seguir. Você pode utilizar a applet da Sagemath disponibilizada no Moodle. Em cada caso, esboce seu gráfico no intervalo
Ver solução completaQuestão 35
Obtenha a série de Fourier em cossenos de cada uma das funções a seguir. Você pode utilizar a applet da Sagemath disponibilizada no Moodle. Em cada caso, esboce seu gráfico no intervalo
Ver solução completaQuestão 36
Obtenha a série de Fourier em cossenos de cada uma das funções a seguir. Você pode utilizar a applet da Sagemath disponibilizada no Moodle. Em cada caso, esboce seu gráfico no intervalo
Ver solução completaQuestão 37
Obtenha a série de Fourier em cossenos de cada uma das funções a seguir. Você pode utilizar a applet da Sagemath disponibilizada no Moodle. Em cada caso, esboce seu gráfico no intervalo
Ver solução completaQuestão 38
Obtenha a série de Fourier em cossenos de cada uma das funções a seguir. Você pode utilizar a applet da Sagemath disponibilizada no Moodle. Em cada caso, esboce seu gráfico no intervalo
com .
Ver solução completaQuestão 39
Obtenha a série de Fourier em cossenos de cada uma das funções a seguir. Você pode utilizar a applet da Sagemath disponibilizada no Moodle. Em cada caso, esboce seu gráfico no intervalo
Ver solução completaQuestão 40
Obtenha a série de Fourier em cossenos de cada uma das funções a seguir. Você pode utilizar a applet da Sagemath disponibilizada no Moodle. Em cada caso, esboce seu gráfico no intervalo
Ver solução completaQuestão 41
Os coeficientes de Fourier de se calculam somando os coeficientes correspondentes de e de .
Ver solução completaQuestão 42
Verdadeiro ou falso? Justifique.
A série de Fourier da função é obtida multiplicando cada termo na série de Fourier de por .
Ver solução completaQuestão 43
Obtenha a série de Fourier em senos de cada uma das funções a seguir. Você pode utilizar a applet da Sagemath disponibilizada no Moodle. Em cada caso, esboce seu gráfico no intervalo
Ver solução completaQuestão 45
Obtenha as séries de Fourier das funções abaixo sem calcular nenhuma integral.
(d)
Ver solução completaQuestão 47
Determine a ordem das equações a seguir. Classifique-as em lineares ou não lineares e especifique se cada equação linear é ou não homogênea.
;
Ver solução completaQuestão 48
Calcule as transformadas de Fourier das funções abaixo.
se e caso contrário.
Ver solução completaQuestão 51
Mostre que a transformada de Fourier de será uma função real se, e somente se, for uma função par.
Ver solução completaQuestão 53
Calcule a série de Fourier das funções a seguir, definidas no intervalo .
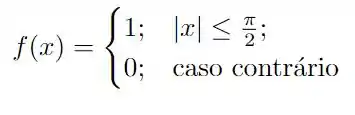
Questão 54
Determine a transformada de Fourier inversa das funções a seguir utilizando a tabela de transformadas vista em sala de aula.
Ver solução completaQuestão 55
Obtenha as séries de Fourier das funções abaixo sem calcular nenhuma integral.
- ;
Questão 56
Obtenha as séries de Fourier das funções abaixo sem calcular nenhuma integral.
(b)
Ver solução completaQuestão 57
Obtenha as séries de Fourier das funções abaixo sem calcular nenhuma integral.
(c)
Ver solução completaQuestão 58
Determine a forma complexa das séries de Fourier das funções a seguir, definidas no intervalo [−π, π].
Ver solução completa
Questão 60
Seja
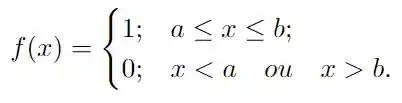
Qual relação deve haver entre e para que a parte imaginária de valha zero para qualquer calor de ?
Ver solução completaQuestão 61
Determine a transformada de Fourier das funções a seguir utilizando a tabela de transformadas vista em sala de aula.
Ver solução completaQuestão 62
Suponha que definimos a transformada de Fourier pela expressão
Qual será neste caso a fórmula para a transformada de Fourier inversa?
Ver solução completaQuestão 63
Determine a transformada de Fourier das funções a seguir utilizando a tabela de transformadas vista em sala de aula.
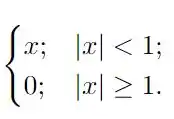
Questão 64
Determine a transformada de Fourier das funções a seguir utilizando a tabela de transformadas vista em sala de aula.
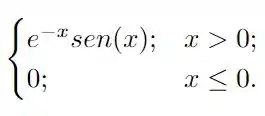
Questão 65
Determine a transformada de Fourier das funções a seguir utilizando a tabela de transformadas vista em sala de aula.
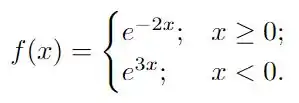
Questão 66
Determine a transformada de Fourier inversa das funções a seguir utilizando a tabela de transformadas vista em sala de aula.
Ver solução completaQuestão 68
Determine a série de Fourier das funções a seguir.
estendida de forma -periódica;
Ver solução completaQuestão 74
Calcule a série de Fourier das funções a seguir, definidas no intervalo .
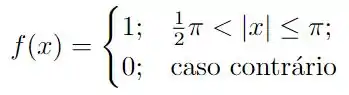
Questão 75
Para cada uma das funções abaixo, definidas no intervalo , obtenha sua série de Fourier e esboce seu gráfico no intervalo .
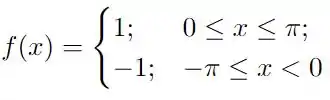
Questão 76
Para cada uma das funções abaixo, definidas no intervalo , obtenha sua série de Fourier e esboce seu gráfico no intervalo .
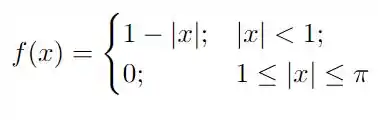
Questão 78
Determine a forma complexa das séries de Fourier das funções a seguir, definidas no intervalo [−π, π].
Ver solução completa