Equações de Maxwell
Produzido por Bruno SoaresTeoria
As Equações de Maxwell, ou Leis de Maxwell são um conjunto de equações que descrevem o comportamento dos campos elétricos e magnéticos, como eles são gerados e qual a relação entre eles.
Indo direto ao ponto, as Equações de Maxwell podem ser escrita das seguintes formas:

-Beleza, mas esse monte de fórmula significa? E pra que que servem as Leis de Maxwell?
Calma, a gente vai entender tudo, timtim por timtim! Se liga nesse vídeozinho super completo sobre as Leis de Maxwell! 👇 🧡
Ou, se você preferir, continua comigo no textinho!
Lei de Gauss
A lei de Gauss nos dá a relação entre um campo elétrico gerado por cargas elétricas. Pra ficar mais claro, você pode imaginar uma superfície fechada com uma carga elétrica dentro, assim:
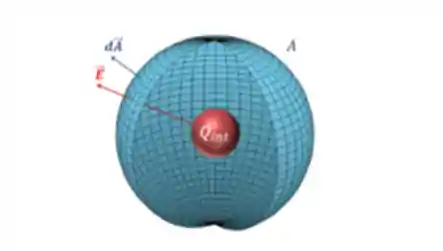
A forma integral da lei de Gauss é:
Onde:
é o campo elétrico gerado por ; é a diferencial da superfície fechada ; é o somatório de cargas dentro da superfície fechada; é a permissividade no vácuo, igual a
Ah, também temos algumas equações auxiliares que podem ajudar nos exercícios:
Podemos também escrever a Lei de Gauss na sua forma diferencial:
No vácuo teremos
Lei de Gauss para o Magnetismo
A lei de Gauss para o Magnetismo diz que o Fluxo Magnético
O raciocínio é bem parecido com a lei de Gauss, mas dessa vez colocamos um imã em uma superfície fechada e analisamos o campo magnético gerado:
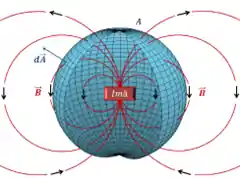
O fluxo magnético será nulo, na prática, isso nos diz que não existem polos magnéticos isolados, ou seja, sempre que tivermos um polo norte, teremos um polo sul.
Sua equação na forma integral é dada por:
Podemos também escrever a Lei de Gauss para o Magnetismo na sua forma diferencial:
Basicamente estamos dizendo que o divergente de
Lei de Faraday-Lenz
A lei de Faraday descreve a relação entre o campo elétrico e o campo magnético. Na prática um campo magnético que varia ao longo do tempo gera um campo elétrico. Esse princípio é utilizado nos geradores elétricos!
A forma integral da Lei de Faraday-Lenz é dada por:
Podemos escrever também a sua forma diferencial:
Lei de Ampère-Maxwell
A lei de Ampère-Maxwell é uma junção da Lei de Ampère com uma correção de Maxwell. Dessa forma, a lei de Ampère afirma que campos magnéticos podem ser gerados através de correntes elétricas e segundo Maxwell e os campos magnéticos também podem ser gerados por campos elétricos que variam ao longo do tempo.
Podemos escrever a Lei de Ampère-Maxwell na sua forma integral:
Ou na sua forma diferencial:
No vácuo temos
Agora vamos praticar com exercícios?!