Propriedades Ondulatórias da Luz
Teoria
O que é a Luz?
A luz é uma onda eletromagnética!
E é isso, acabou esse tópico. Tudo ok? Não? Tá, vamos explicar melhor.
Quando um campo elétrico varia com o tempo, oscilando, ele induz um campo magnético. Esse campo magnético também varia com o tempo, oscilando, e isso faz ele induzir o campo elétrico. Assim, eles se auto-sustentam!
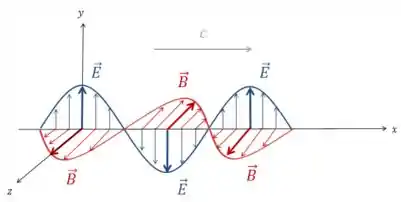
Isso é uma onda eletromagnética.
Ondas eletromagnéticas estão por toda parte! São usadas para transmissões de TVs, rádios, usadas em fornos micro-ondas...
E como falamos antes, elas constituem a luz visível (luz do sol, lâmpadas, etc).
Propriedades Ondulatórias da Luz
A luz é uma onda, e como toda boa onda, ela possui propriedades ondulatórias como frequência, comprimento de onda e amplitude.
Ondas eletromagnéticas são ondas transversais, pois os campos elétrico e magnético oscilam perpendicular em relação a direção de propagação da onda. Além disso, como eles induzem um ao outro, eles estão sempre em fase entre si:
- Quando tem o seu valor máximo, também tem o seu valor máximo. Quando é nulo, também é nulo.
Podemos descrever os campos elétrico e magnético das ondas eletromagnéticas por funções senoidais (função seno ou função coseno). Assim, temos:
Agora que estamos lidando com ondas, é muito importante lembrar quem é quem, e a relação entre eles.
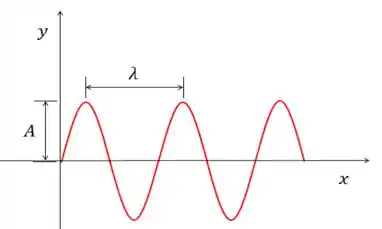
O comprimento de onda é a distância entre duas cristas consecutivas. A amplitude da onda é a amplitude máxima de oscilação. A frequência da onda é o número de oscilações que a onda faz num determinado período de tempo.
Nas nossas funções, a amplitude do campo elétrico é , enquanto que a do campo magnético é .
A velocidade de uma onda é dada por , onda para nós, .
A velocidade da luz no vácuo é de aproximadamente .
Tá, mas será que esse valor veio do nada? A verdade é que não, já se provou que a velocidade da luz no vácuo é dada por:
Sendo a permissividade no vácuo e a permeabilidade no vácuo.
Essa relação também é válida para outros meios, portanto, você pode encontrar a velocidade da luz (ou de qualquer onda eletromagnética) em um meio, fazendo:
Onde e são a permissividade e a permeabilidade do meio.
Na equação com cosseno, as propriedades que aparecem são o número de onda e a frequência angular .
Também podemos obter a velocidade da luz com esses dois fatores.
Propriedades Específicas de Ondas Eletromagnéticas (Luz)
Vou te falar algumas propriedades que são muito importantes para termos uma ideia melhor de como essas ondas funcionam. Vamos lá!
- O produto vetorial entre o campo elétrico e o campo magnético, , sempre vai apontar na direção e no sentido de propagação da onda.
- A relação entre o módulo campo elétrico e o módulo campo magnético de uma onda eletromagnética que se propaga no vácuo é sempre a mesma, em qualquer instante e em qualquer ponto do espaço! Essa relação é dada por:
- Como e estão em fase, podemos cortar os cosenos da igualdade anterior e relacionar as amplitudes:
- A onda eletromagnética se desloca no vácuo com velocidade constante e igual à velocidade da luz.
- Ondas eletromagnéticas não necessitam de meio material pra se propagar. Assim, os únicos valores que oscilam nela são o campo elétrico e o campo magnético.
Isso acontece em parte porque os campos elétricos e magnéticos são perpendiculares entre si e em relação à direção de propagação da onda, e em outra parte pela regra da mão direita.
Lembrando que é a velocidade da luz no vácuo, que vale aproximadamente
Se liga!
A relação é válida quando a onda se propaga no vácuo!
Se ela se propaga em qualquer outro meio, então a relação passa a ser:
Frentes de Onda
Vamos escolher um ponto da onda eletromagnética em um dado tempo, e tentar andar junto com ela. (Aviso: Não faça isso em casa. Você não vai conseguir andar na velocidade da luz!)
Podemos imaginar que nós andando junto com esse parceiro ponto da onda somos o plano da figura abaixo.
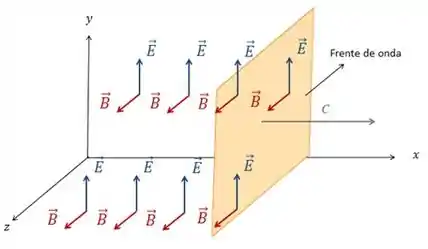
Como estamos juntos da onda, nós não vemos mais as oscilações do campo elétrico e do campo magnético. Só vemos e num valor constante.
Este plano que imaginamos, onde e são constantes é o que chamamos de frente de onda.
Usando lá as nossas funções senoidais, isso equivaleria a ter o cosseno constante e pra isso eu preciso que seu argumento seja constante. Logo, na frente de onda, temos:
Espectro Eletromagnético
E afinal, qual a diferença entre ondas de rádio, microondas, infravermelho, ultravioleta, luz,... ?
Dependendo da sua frequência (ou do seu comprimento de onda, dá na mesma), as ondas eletromagnéticas têm diferentes usos e, por isso, ganham nomes específicos. Nós representamos isso pelo espectro eletromagnético.
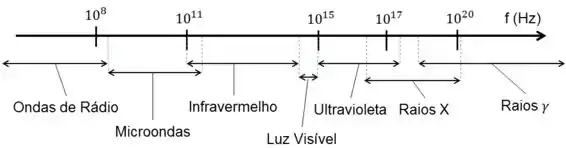
Show! Agora que entendemos melhor as regras, podemos ir pro jogo!
Propriedades Ondulatórias da Luz
Propriedades Específicas de Ondas Eletromagnéticas (Luz)
Frentes de Onda
Espectro Eletromagnético
Exercícios Resolvidos
Exercício Resolvido #1
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 27-1
Se o campo magnético de uma onda luminosa é paralelo ao e seu módulo é dado por , determine:
- A direção de propagação da onda
- A direção do campo elétrico associado à onda.
Passo 1
Letra a)
Como a única variável espacial da qual o campo magnético depende é , então a direção de propagação é o .
Passo 2
Letra b)
Sabemos que a direção de propagação, o campo magnético e o campo elétrico são todos perpendiculares entre si.
Assim, como é paralelo ao e a propagação é paralela ao , a reta perpendicular a eles é o . Com isso, o campo elétrico vai ser paralelo ao .
Por fim, para saber o sentido.
Sabemos que a propagação é no mesmo sentido que . Porém, não sabemos qual sentido da propagação.
Vamos encontrar isso pelo valor dentro do seno. Para a nossa frente de onda () se manter constante, quando o tempo passar, o valor de tem de aumentar. Logo, a onda se propaga no sentido positivo do eixo .
Usando a regra da mão direita para multiplicar e , para dar o sentido da propagação temos que ter no sentido positivo do .
Resposta
Letra a)
A onda se propaga ao longo do .
Letra b)
O campo elétrico oscila ao longo do sentido positivo do .
Exercício Resolvido #2
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 37-86
Uma onda eletromagnética está se propagando no sentido negativo do no vácuo, ou seja, a sua velocidade é .
Em um certo local e em um certo instante o campo elétrico aponta no sentido positivo do e tem um módulo de . Determine:
- O módulo do campo magnético correspondente.
- A direção do campo magnético correspondente.
Passo 1
Letra a)
Uma das relações mais importantes para lembrarmos é:
Assim, tendo o módulo do campo elétrico, temos o módulo do campo magnético.
Substituindo os valores:
Passo 2
Letra b)
A onda eletromagnética se propaga numa direção paralela ao produto vetorial e com o mesmo sentido.
Como a direção é o no sentido negativo, então esse produto vetorial vai ser na direção e sentido .
está no sentido positivo do (), e usando a regra da mão direita sabemos que ao colocar a mão paralela a e “dar um tapa” em , o nosso dedão apontaria pra .
Para isso, tem que estar no sentido negativo do . De fato:
Resposta
Letra a)
O módulo do campo magnético é .
Letra b)
A direção e sentido do campo magnético é o sentido negativo do .
Exercício Resolvido #3
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 37-79, modificado
A componente elétrica de um feixe de luz é dada por
- Escreva uma expressão para a componente magnética da onda, incluindo o valor de .
- O comprimento de onda da luz.
- O período da luz.
- O campo magnético oscila paralelamente a que eixo?
- Em que região do espectro eletromagnético está essa onda?
Determine:
Passo 1
Letra a)
Essa pergunta tem duas partes: a primeira é encontrar o valor de e a segunda é escrever a expressão do campo magnético que corresponde a esse campo elétrico.
Vamos começar achando .
A velocidade da onda é dada por:
A velocidade da luz é uma constante, . O número de onda é dado no enunciado, dentro do seno, . Assim, podemos achar a frequência angular.
Passo 2
O segundo passo é achar a expressão para o campo magnético. Tem uma relação que nos dá exatamente a amplitude do campo magnético a partir do campo elétrico.
Assim, .
Dividindo a amplitude pela velocidade da luz:
Passo 3
Letra b)
Para achar o comprimento de onda, temos a relação entre ele e o número de onda.
Como , temos:
Passo 4
Letra c)
Para achar o período, usamos a frequência angular.
Como encontramos na letra a, .
Passo 5
Letra d)
Vejamos a direção e sentido do campo magnético .
No enunciado, vemos que essa é a componente de no . Além disso, como ele depende de , a propagação se dá na direção do .
Porém, para frente de onda se manter constante com o passar do tempo, o valor de precisa diminuir. Logo, a onda se propaga no sentido negativo do .
Usando a regra da mão direita para ver como pode estar no sentido negativo do , temos que ter no sentido positivo do .
Passo 6
Letra e)
Transformando o comprimento de onda em frequência, temos:
Essa frequência corresponde à região do infravermelho.
Resposta
Letra a)
Letra b)
Letra c)
Letra d)
O campo magnético oscila no sentido positivo do .
Letra e)
Essa onda está na região do infravermelho no espectro eletromagnético.
Exercício Resolvido #4
UFRJ, Física 4, Profa. Regina Celia Arcuri, Lista de Exercícios 2
O campo elétrico de uma onda eletromagnética é dado por:
As unidades de x e t são metros e segundos respectivamente.
- Qual é o comprimento de onda em cm?
- Qual é a frequência em Hz?
- Qual é a velocidade em ?
- Calcule o valor máximo do campo magnético em teslas ();
- Determine
Passo 1
Letra a)
Analisando a equação do campo elétrico, podemos notar que o número de onda vale .
Logo, podemos calcular o comprimento de onda .
O problema nos pede para calcular em cm. Assim,
Passo 2
Letra b)
A partir da equação dada, podemos notar que a frequência angular vale .
Agora podemos encontrar a frequência .
Passo 3
Letra c)
Precisamos calcular a velocidade em .
Já que conhecemos os valores de e , podemos calcular .
Agora precisamos passar de para . Fazemos isso multiplicando a velocidade por . Logo,
Passo 4
Letra d)
Precisamos calcular o valor máximo do campo magnético .
O módulo do campo elétrico está relacionado com o módulo do campo magnético através da equação:
Onde é a velocidade da luz no meio, que vale a (de acordo com o Passo 3).
Assim, acharemos o valor de quando utilizarmos o valor máximo do campo elétrico na equação acima.
Analisando a equação do campo elétrico dado pelo problema
Vemos que o valor máximo dele será
Já que a função varia entre 1 e -1. Logo,
Vale chamar a atenção para um detalhe!
Estamos acostumados a utilizar a relação , mas esta equação vale apenas quando a onda se propaga no vácuo, já que é a velocidade da luz no vácuo.
Mas como não foi especificado o meio que estamos observando e já havíamos calculado a velocidade no item anterior, então utilizamos essa velocidade.
Então fica esperto! Se ele não falar o meio em que a onda eletromagnética está se propagando, vale a pena conferir a velocidade, pode ser o diferencial em uma questão! ;)
Passo 5
Letra e)
Para calcularmos o vetor de campo magnético , temos que saber a direção de propagação da onda e o eixo de oscilação do campo magnético.
Analisando o campo elétrico
Podemos fazer a seguinte análise para descobrir a direção e sentido de propagação da onda:
Analisando o argumento
Para que ele permaneça constante, conforme o tempo aumenta, é necessário que o valor de diminua, conseguiu ver?
Logo, a onda se propaga no sentido (sentido negativo de ).
Sabendo que o campo elétrico tem o sentido (de acordo com a própria equação), podemos usar a regra da mão direita para saber o sentido de , já que o produto vetorial nos dá o sentido de propagação da onda.
Assim, tem o sentido de , porque
Confere aí! ;)
Portanto o vetor , é dado por
Resposta
Letra a)
Letra b)
Letra c)
Letra d)
Letra e)
Exercício Resolvido #5
UFRJ , Física 4, Prof. Marcelo Araújo, Prova 1 de 2008.1
Dada a onda eletromagnética:
Onde é uma constante. Ache o campo magnético
Passo 1
Primeiro, temos que saber a direção e sentido de propagação da onda eletromagnética.
Vemos isso através da análise do argumento
A partir do argumento acima, descobrimos que a onda se propaga no eixo .
Mas para saber o sentido de propagação, temos que fazer a seguinte análise:
Para que o argumento permaneça constante, conforme o tempo aumenta, é necessário que o valor de também aumente, conseguiu ver isso?
Assim, a onda se propaga no eixo , no sentido .
Logo, quando fizermos o produto vetorial , o resultado poderá ter uma componente apenas na direção
Passo 2
Usando a regra da mão direita, podemos descobrir a direção e o sentido que as componentes devem ter para que o produto vetorial tenha sempre o sentido .
possui componentes em e .
Lembre que:
Logo, deve possuir componentes em e .
Podemos escrever também que,
Já que . Caso a onda se propagasse no vácuo, teríamos .
Resposta
Exercício Resolvido #6
USP, Prova 1, 2013.3
A figura abaixo representa os campos elétrico e magnético de uma onda eletromagnética plana monocromática, no vácuo, na origem do sistema de coordenadas em dois instantes diferentes. Nestes dois momentos . A frequência da onda é e sua velocidade de propagação .
Determine o sentido de propagação da onda. Calcule o comprimento de onda , a frequência angular e o número de onda .
Escreva a expressão completa do vetor campo elétrico indicando a dependência nas coordenadas e no tempo.
Escreva a expressão do campo magnético associado ao campo elétrico dado.
Passo 1
Determine o sentido de propagação da onda. Calcule o comprimento de onda , a frequência angular e o número de onda .
Para determinar o sentido de propagação da onda, é importante você lembrar que o produto vetorial entre e aponta na mesma direção e sentido de propagação da onda.
Em , aponta no sentido vetor e o vetor aponta no sentido , logo:
Assim, a onda se propaga na mesma direção e sentido do vetor .
Passo 2
Aqui precisamos lembrar de algumas fórmulas que, vira e mexe, aparecem na nossa vida:
Bom, acho que com isso aqui a gente começa a se virar.
O problema nos deu e , então podemos começar calculando , usando a primeira fórmula.
Então vamos aproveitar o embalo e calcular o número de onda
Pra fechar, vamos calcular a frequência angular .
Passo 3
Escreva a expressão completa do vetor campo elétrico indicando a dependência nas coordenadas e no tempo.
Os dois gráficos mostram que o campo elétrico se propaga na direção .
Logo, a expressão do vetor campo elétrico vai ter essa cara:
Obs.: O sinal aqui é positivo porque a onda se propaga no sentido do vetor . Se ela se propagasse no sentido do vetor , por exemplo, o sinal seria negativo . Ou seja, o sinal é sempre do contra!
Ok, dessa expressão, as únicas coisas que não sabemos são os valores de e de , então vamos utilizar as condições de contorno pra encontrar esses valores, ok?
- ;
- ;
Ok! Agora vamos trabalhar com esses caras!
Passo 4
Dividindo as duas equações, teremos:
Opa! Substituindo esse cara em uma das situações, teremos:
Finalmente, o campo elétrico será dado por:
Acabou, mas se quiser ajeitar esse cara pra ficar melhor, podemos reescrevê-lo assim:
Passo 5
Escreva a expressão do campo magnético associado ao campo elétrico dado.
Os dois gráficos mostram que o campo magnético se propaga na direção .
Mas como saber se o campo magnético está no sentido de ou de ??
Já sabemos que o campo elétrico está no sentido de e que a onda se propaga no sentido de . Então agora é só testar:
Sendo assim, o campo magnético se propaga no sentido de .
Logo, a expressão do vetor campo elétrico vai ter essa cara:
Já temos todos os dados, exceto . Mas aqui, basta lembrar que:
Finalmente:
Resposta
A onda se propaga na mesma direção e sentido do vetor .