Propagação das Ondas Eletromagnéticas
Produzido por Bruno SoaresTeoria
Em alguns exercícios de encontrar as propriedades ondulatórias da luz, pode ser que surjam, dentro da função cosseno, não só uma variável espacial , mas duas variáveis e .
Nestes casos, como encontrar a direção de propagação e o comprimento de onda da luz?
Ondas Eletromagnéticas numa direção qualquer
Quando a onda se propaga paralela a um dos eixos cartesianos, o campo elétrico ou o campo magnético vão sempre depender apenas do tempo e da variável correspondente ao eixo. Por exemplo:
O campo elétrico depende apenas de , logo a onda se propaga paralelamente ao eixo .
Mas como ficaria minha equação caso a onda se propagasse numa direção qualquer?
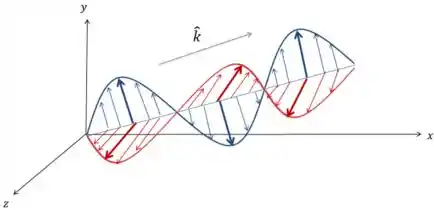
A onda está se propagando na direção e sentido do vetor unitário . Uma forma de escrever esse vetor de propagação é:
Em geral, a gente não precisa dessa fórmula pra fazer exercícios. Mas eu quis deixar claro que a onda eletromagnética se propaga no sentido do produto vetorial de e ! E isso sim é importante.
Agora, vamos definir um vetor que tenha a mesma direção e sentido de , mas multiplicado pelo número de onda.
O motivo de a gente falar desse vetor é que agora a função senoidal que descreve os campos elétrico e magnético vai sofrer uma pequena mudança.
Nesta nova equação, é como se fosse o número de onda, nos dando também a direção e o sentido da onda. Usamos no lugar de para o ponto do espaço onde estou olhando. O vetor unitário é a direção de vibração do campo elétrico, sendo perpendicular a .
A operação é o produto interno entre e .
Vamos deixar mais concreto. Digamos que a onda se propague no , fazendo um ângulo de com o eixo .
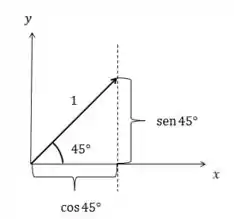
Essa direção é dada pelo vetor unitário . Digamos que o comprimento de onda da luz seja dado por
Assim:
E aí está, desvendado o mistério da dependência com !
Quando o campo elétrico ou o campo magnético depender de mais de uma coordenada, é porque a direção de propagação da onda não é paralela a nenhum eixo.
Notação complexa
Como a gente tem muitos senos e cossenos nessa matéria às vezes é conveniente usar notação diferente chamada de notação complexa. Nada mais é que pegar uma função exponencial de número complexo
Essa exponencial complexa se relaciona com senos e cossenos por meio da fórmula de Euler
A ideia da notação complexa é simplificar a notação (perdão a piadinha hahaha)
Funciona assim:
Vamos supor que você tem o seguinte campo
A forma de escrever usando números complexos é
Quando quiser recuperar o campo original é só pegar a parte real desse número, que será a parte com cosseno
Tá, saquei. Mas de que isso me adianta?
Tem duas vantagens! A primeira é que derivadas ficam mamão com açúcar de fazer por que é a derivada de uma exponencial!
Ex:
A segunda é que fica mais compacto e fica mais fácil pra somar campos
Ex: Supondo que temos dois campos de mesma intensidade
Se quisermos somar os dois temos
Botando o em evidência temos
Pela definição da exponencial complexa
Assim
E agora, vambora pros exercícios?
Notação complexa
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ, Física 4, Prova 1, 2012.1, modificado
Uma onda eletromagnética senoidal plana se propagando no ar possui comprimento de onda igual a e a amplitude do campo elétrico é igual a .
Dê as suas respostas em valores numéricos.
- Qual é a frequência desta onda?
- Sabendo que o vetor de propagação da onda está na mesma direção e é proporcional ao vetor , escreva uma possível expressão para o vetor campo elétrico em função do tempo e do espaço.
- A partir da sua resposta do item b), escreva uma possível expressão para o vetor campo magnético em função do tempo e do espaço.
Passo 1
Letra a)
O problema nos dá o comprimento de onda , a amplitude do campo elétrico e nos pede a frequência da onda .
Para descobrir o valor de podemos usar a seguinte relação:
Onde:
;
;
Logo:
Passo 2
Letra b)
O vetor de propagação da onda está na mesma direção e é proporcional ao vetor .
Sabendo que o vetor de campo elétrico deve ser perpendicular à direção de propagação, podemos colocar o campo elétrico no sentido do vetor .
Sabemos também que uma onda eletromagnética senoidal possui um campo elétrico do tipo:
Nesse caso, aparece um pois a onda se desloca tanto no sentido quanto no sentido .
Em casos como esse, dizemos que
Relaxa! Eu sei que isso é novo! Mas é importante você lembrar disso, porque questões como esta e a anterior costumam cair bastante!
Assim, o número de onda é calculado por
Onde:
;
;
Logo:
Como:
Se a gente fizer o produto:
Como dissemos anteriormente, podemos calcular o valor de através da seguinte relação:
Onde:
;
Logo:
Como o problema nos diz que vale , agora podemos, finalmente, escrever o vetor campo elétrico , dado por:
Passo 3
Letra c)
O vetor de propagação da onda está na mesma direção e é proporcional ao vetor .
Sabemos que o vetor de campo elétrico deve ser perpendicular à direção de propagação , e perpendicular ao vetor campo elétrico .
Daqui se supormos que o unitário do campo magnético seja , então, usando o produto escalar, vamos ter
Como esse produto escalar tem que ser nulo, já achamos que
Para achar as outras duas componentes podemos usar tanto quanto
Usando
Portanto:
Ou usando
Como o vetor tem que ser unitário
Assim finalmente o unitário do campo magnético será
Sabemos esta onda eletromagnética senoidal possuirá um campo magnético do tipo:
Onde:
;
Resposta
Letra (a):
Letra (b):
Letra (c):
Exercício Resolvido #2
UFRJ, Física 4, Prova 1, 2015.1
É conhecido que um campo elétrico de uma onda plana eletromagnética propagando-se num meio dielétrico (onde ) é dado por
onde , e .
Obs: As relações e as equações para uma onda eletromagnética num meio dielétrico são as mesmas que para uma onda eletromagnética no vácuo, substituindo apenas nas relações a velocidade da onda eletromagnética no vácuo pela velocidade da onda eletromagnética no meio dielétrico.
- Qual é o vetor unitário da direção propagação da onda?
- Calcule o vetor campo magnético da onda.
Passo 1
Qual é o vetor unitário da direção propagação da onda?
No fundo, nós poderíamos reescrever o vetor campo elétrico da seguinte forma:
O termo está associado à direção de propagação da onda, e .
Eu sei que essa não é uma notação que aparece sempre, mas acaba sendo válida principalmente nos casos que a onda não se propaga em uma direção paralela a um dos eixos coordenados.
Como todo o vetor, podemos reescrever o vetor da seguinte forma:
Substituindo isso na expressão do campo elétrico, teremos:
Agora vamos comparar com a expressão do campo elétrico dado pelo problema:
Comparando essas suas expressões, podemos dizer que:
Logo:
Ou:
Passo 2
Calcule o vetor campo magnético da onda.
Uma forma de calcular o campo magnético utilizando o vetor , é através da expressão:
Tem um detalhe importante que não dá pra esquecer, a onda está se propagando em um meio dielétrico, então ao invés de usarmos , teremos que usar para a velocidade da luz no meio, onde:
Agora já podemos calcular o campo magnético.
Como os números são meio esquisitos, para não nos confundirmos, uma boa é ir substituindo aos poucos. Vamos começar organizando esse cara:
Agora podemos substituir os valores de , , e .
Finalmente:
Resposta
Exercício Resolvido #3
Elaboração própria
Uma onda eletromagnética possui módulo do campo magnético e frequência , sabendo que o vetor de propagação da onda está no mesmo sentido e é proporcional a , escreva uma expressão para o vetor campo magnético e determine o comprimento de onda.
Passo 1
Primeiro bora encontrar o comprimento de onda, podemos usar essa relação:
Com e temos:
Passo 2
Agora podemos começar a pensar no campo magnético.
Se o nosso vetor do sentido da onda é proporcional a , o sentido de só pode ser , pois é diferente do sentido de propagação da onda.
Se a onda tem sentido e , temos um que é dado por:
O é a constante de fase que é dada por:
Beleza, agora vamos encontrar o valor do módulo do vetor se temos .
Vamos encontrar a resultante com os termos que acompanham os vetores unitários:
Assim, conseguimos determinar o :
Simplificando
Passo 3
Maneiro, agora faremos um produto escalar de e já que a expressão pro campo magnético genérica é:
Assim:
Beleza, temos quase tudo. Só falta a frequência ângular que é:
Agora é só substituir tudo e se liga que osentido do campo deve ser perpendicular ao sentido da onda e portanto está na direção
Show! Acabamos! :D
Resposta
Exercício Resolvido #4
Elaboração própria
Usando a notação complexa, some os campos elétricos abaixo:
Sendo e
Passo 1
Pode parecer meio confuso somar todas essas coisas diferentes, então bora deixar todos esses campos bem parecidos pra gente converter para notacão complexa e somá-los.
Usando a identidade trigonométrica podemos deixar também com função cosseno, isso é interessante para somarmos depois.
Vamos deixar também os campos em função do menor deles, visando não trabalharmos com frações.
Substituindo também no que , assim:
Passo 2
Vamos passar os vetores para a notação complexa, assim poderemos somá-los.
Para passar pra notacão complexa, o macete é trocar a trigonométrica pelo número de euler e elevarmos esse número a vezes o argumento da trigonométrica. Fazendo isso temos pro vetor :
Fazendo isso para os outros vetores teremos:
Passo 3
Maneiro, agora com todo mundo na notação complexa é só somar os vetores.
Arrumando isso, podemos deixar em evidência.
Podemos melhorar isso um pouco, colocando também o em evidência, assim temos: