Problemas Estaticamente Indeterminados
Produzido por Pablo RicardoTeoria
Revisão
Vamos dizer que você precisa descobrir a tensão normal em uma coluna de concreto.
Essa coluna está entre entre uma placa rígida e o solo, que também é rígido, e está sob compressão por uma carga :

Esse é um problema de carga axial: as forças na coluna agem ao longo do seu eixo principal.
Agora lembra aí...
Quando a gente estudou tensões, vimos que para encontrar a tensão normal média nesse coluna, precisamos conhecer a força interna normal nela.
E, para encontrar a força interna , podemos usar os métodos da estática:
- Fazer um DCL (diagrama de corpo livre) da coluna;
- Aplicar as condições de equilíbrio na coluna;
- E fazer uma análise dos esforços internos nela.
Problemas Estaticamente Indeterminados
Agora, vamos dizer que ao cortar essa coluna ao meio, você descobre que ela possui uma viga de aço interna:
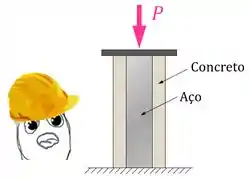
Isso significa que na hora de fazer o DCL dessa coluna, vamos precisar fazer um DCL para cada material.
Fazendo isso, vemos que parte da compressão vai para o concreto através da força e outra parte vai para o aço através da força :
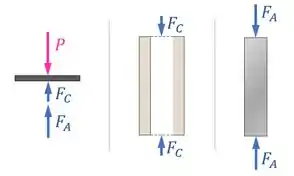
E aí aqui as coisas dificultam:
Nós só temos uma equação de equilíbrio (o equilíbrio das forças verticais na placa rígida) que nos permite relacionar as forças desconhecidas e com a carga :
Com uma única equação, não é possível determinar as duas incógnitas e .
Ou seja, essa estrutura é estaticamente indeterminada: os métodos da estática (DCL, equilíbrio, etc.) não são o suficiente para determinar o que está acontecendo nela.
Então precisamos encontrar alguma outra equação que relacione e para que a gente possa determinar o valor dessas compressões.
Mas como é que a gente consegue essa outra equação?
Compatibilidade
Bom, se as condições de equilíbrio não são suficientes para achar as incógnitas, podemos pensar na compatibilidade entre as variações de comprimento das peças.
Para a nossa coluna, por exemplo:
Se o aço sofre uma variação de comprimento , o concreto vai ter que sofrer uma variação igual para que a placa rígida continue em contato com os dois materiais:
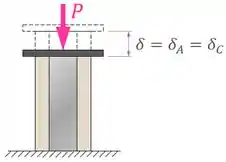
Agora, se nos lembrarmos do que vimos em deformação, vamos lembrar que existe uma fórmula para a variação de comprimento em uma peça sob carregamento axial:
(Lembra? Essa fórmula vem da união das definições de tensão normal média e de deformação com a Lei de Hooke .)
Como o concreto e o aço estão sob compressão pura por forças e , as forças normais neles vão ser:
E, olha só, se a gente juntar a relação , a fórmula e esses valores de , achamos que:
O que é uma outra equação relacionando as incógnitas e !
Combinando essa equação nova com a anterior , conseguimos determinar as compressões (e, em seguida, as tensões) no concreto e no aço!

Equação de Compatibilidade
Essa relação entre as variações de comprimento é o que chamamos de equação de compatibilidade.
Diferentes exercícios vão ter diferentes equações de compatibilidade, sendo que alguns vão ter até mais de uma.
Para encontrar uma equação de compatibilidade de um exercício, o bizu é:
- Fazer um desenho (no papel ou mentalmente) de como vai ficar o problema depois que as peças se deformarem;
- E encontrar nesse desenho alguma relação (de igualdade ou de semelhança de triângulos) entre as variações de comprimento de cada peça.
Para alguns exercícios, existe um método para encontrar a equação da compatibilidade que deixa as coisas mais fáceis de visualizar!
:P
É o método de análise de força (também conhecido como método da superposição!), que é o que vamos ver a seguir.
Método de Análise de Força
Para aprender esse método, vamos considerar a barra abaixo, engastada no ponto e carregada com uma força conhecida:
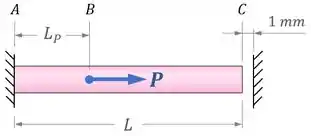
Vamos dizer que a gente descobriu que essa força vai gerar na barra uma deformação maior que a folga de . (Ou seja, o ponto da barra vai encostar na parede da direita.)
Com isso, a barra vai sofrer reações das paredes tanto em quanto em :
![]()
E, como todas essas forças agem na horizontal da barra, a única condição de equilíbrio disponível vai ser o equilíbrio de forças na horizontal:
Dessa forma, o exercício é estaticamente indeterminado, já que essa única equação não é suficiente para encontrarmos o valor das reações desconhecidas e .
Para encontrar e , vamos precisar de uma equação de compatibilidade. O método de análise de força vai nos ajudar a encontrar isso.
1º Passo - Reações Redundantes
O primeiro passo para aplicar o método é retirar reações da peça até que ela deixe de ficar estaticamente indeterminada.
Essas reações que forem retiradas vão ser chamadas de reações reduntantes.
No caso da nossa barra, podemos, por exemplo, escolher retirar a reação .
Fazendo isso, vamos ter uma reação desconhecida () e uma equação de equilíbrio (). Dessa forma, a barra vai ficar estaticamente DEterminada.
2º Passo - Diagramas de Carregamento e de Reação Redundante
O próximo passo é esboçar, rapidamente, alguns diagramas.
O primeiro vai ser o diagrama de carregamento, que é o diagrama da peça sem as reações redundantes:
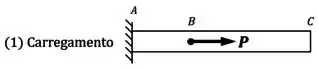
Em seguida, desenhamos um diagrama para cada reação redundante (no nosso caso, só temos uma, que é ).

Feito isso, indicamos, nos mesmos esboços, as deformações causadas por cada carregamento:
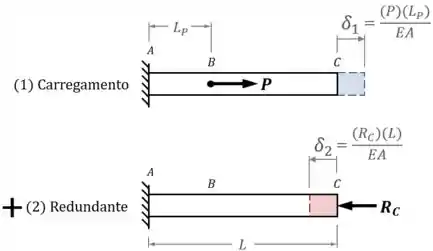
3º Passo - Superposição
Por último, fazemos a superposição das variações de comprimento de cada diagrama para encontrar a variação total de comprimento na peça:
Olhando para a proposição original do problema, vemos que a variação total de comprimento na barra vai ser igual à folga de , de tal forma que:
Essa é a nossa equação de compatibilidade!
Finalização
Por fim, conseguimos descrever em função da força (conhecida) e em função da reação (desconhecida). Dessa forma, conseguimos:
- Usar a equação de compatibilidade para encontrar ;
- E, depois, usar o equilíbrio de forças para encontrar .
E assim resolvemos o exercício!
Princípio da Superposição
O que fizemos no método da análise de força foi aplicar um princípio chamado de Princípio da Superposição.
Basicamente, esse princípio diz que, se a gente dividir um problema em problemas menores, a solução do problema original vai ser a superposição da solução dos problemas menores.
Esse princípio pode ser utilizado para o cálculo de forças, tensões e deformações sempre que os materiais estiverem respondendo de forma linear (de acordo com a Lei de Hooke).
Inclusive, não é necessário você estar usando o método de análise de força para usar o princípio da superposição.
Compatibilidade
Equação de Compatibilidade
Método de Análise de Força
Princípio da Superposição
Exercícios Resolvidos
Exercício Resolvido #1
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 91-4.2.
A coluna de aço A-36 é usada para suportar as cargas simétricas dos dois pisos de um edifício. Determine o deslocamento vertical de sua extremidade, , se , e a coluna tiver área de seção transversal de .
Dados: .
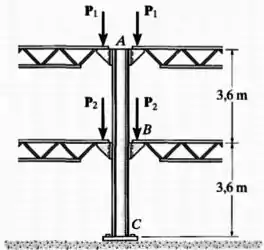
Passo 1
Os pares de forças e estão comprimindo a coluna , que possui uma área de seção transversal e um módulo de elasticidade .
O exercício quer saber o deslocamento da extremidade .
Para encontrar esse deslocamento, podemos:
- Encontrar as forças normais e as variações de comprimento nos trechos e . Nesse caso, vamos ter que ;
- Ou calcular individualmente as variações de comprimento e causadas pelos pares de forças e , respectivamente, e usar o princípio da superposição para definir que .
Aproveitando esse exercício para treinar o princípio da superposição, vamos utilizar o segundo método!
Passo 2
Aplicando o princípio da superposição, podemos calcular individualmente as deformações e , causadas pelos pares de forças e , respectivamente.
E, depois, podemos somar esses efeitos para encontrar a deformação total na coluna:
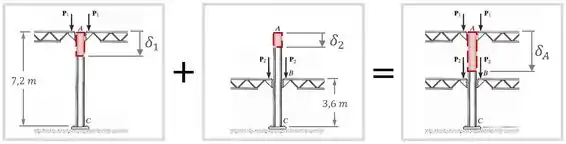
Dessa superposição de efeitos, encontramos que:
Então nos resta encontrar as deformações e causadas por cada carregamento.
Passo 3
Para encontrar a deformação causada pelas forças , vamos pensar na situação em que só as forças estão atuando:
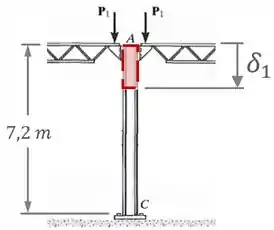
Nesse caso, a coluna vai ser um grande segmento de comprimento , área de seção transversal e módulo de elasticidade .
Além disso, como as únicas forças atuando são as duas forças de compressão, vamos ter que a força normal na coluna vai ser .
Daí que para encontrar a variação de comprimento , podemos usar a fórmula , de tal forma que:
Passo 4
De forma análoga ao passo passado, vamos agora pensar no caso em que somente as forças estão atuando:
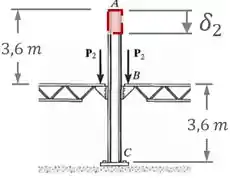
Nesse caso, a coluna vai ser composta por dois segmentos e , ambos com uma área de seção transversal , módulo de elasticidade e comprimento .
Dessa forma, a variação de comprimento na coluna vai ser igual à soma das variações de comprimento de cada segmento:
Fazendo essa soma, temos que:
Agora, enquanto que o segmento vai ter uma força normal , o segmento não vai estar carregado, e vai ter assim uma força normal nula.
Com isso, encontramos que:
Passo 5
Por fim, aplicando a fórmula que tínhamos encontrado anteriormente para superposição dos efeitos, temos que:
Substituindo as expressões encontradas para e :
Arrumando, isso fica assim:
Substituindo , , , , e , temos que:
Para calcular isso, precisamos prestar atenção nas unidades.
Nesse caso, podemos nos lembrar que é o mesmo que . Assim, as unidades e se cortam e o resultado final sai em , que é a unidade que vai sobrar.
Calculando tudo, encontramos então que:
Esse número é bem pequeno, então podemos reescrevê-lo em na hora de darmos a resposta:
Resposta
Exercício Resolvido #2
Ferdinand P. Beer et al., Mecânica dos materiais, 5ª ed. Porto Alegre: AMGH, 2011, pp. 99-2.35.
Forças de compressão centradas de são aplicadas em ambas as extremidades do conjunto mostrado na figura por meio de placas rígidas. Sabendo que e , determine as tensões normais no núcleo de aço e no tubo de alumínio e a deformação do conjunto.
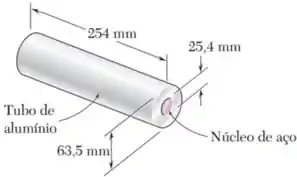
Passo 1
Nesse exercício, temos:
- Um núcleo de aço com diâmetro e módulo de elasticidade ;
- E um tubo de alumínio com diâmetro interno , diâmetro externo e módulo de elasticidade .
Essas duas peças têm um comprimento original e estão sendo comprimidas por uma força por meio de placas rígidas nas suas extremidades:

Além disso, ainda temos que essa compressão por meio de placas rígidas vai causar aço e no alumínio variações de comprimento e iguais:
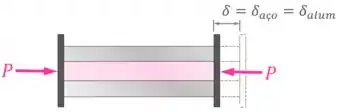
No item , o exercício quer que a gente encontre as tensões normais em cada peça, que vão ser dadas pela fórmula da tensão normal média .
O primeiro passo vai ser fazer um DCL (diagrama de corpo livre) das peças para identificar as forças atuando no aço e no alumínio.
Como as condições de equilíbrio não vão ser suficientes para achar as incógnitas desse DCL, vamos ter que usar também a condição de compatibilidade .
Finalmente, uma vez que tivermos encontrado as forças atuando em cada peça, vamos poder calcular as tensões nelas.
Já no item , o exercício quer saber a deformação do conjunto.
Como as duas peças tem comprimentos originais e variações de comprimento iguais, a deformação nelas vão ser iguais.
Assim, podemos usar a tensão e o módulo de elasticidade de qualquer uma das peças para encontrar a deformação do conjunto usando a Lei de Hooke .
Passo 2
Começamos fazendo o diagrama de corpo livre das peças presentes no exercício:

Com isso, percebemos que uma porção da força de compressão é suportada pelo aço e outra porção é suportada pelo alumínio.
Aplicando as condições de equilíbrio para as placas rígidas, temos que o somatório de forças na horizontal dessas placas deve ser igual a zero:
O que significa que:
O que já era esperado.
Mas infelizmente, essa única equação não é o suficiente para que a gente consiga encontrar as incógnitas e .
Então vamos precisar de uma equação de compatibilidade para complementar essa equação.
Passo 3
Pensando em como as nossas peças vão se deformar:
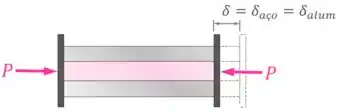
Conseguimos identificar a equação de compatibilidade:
Agora, essa equação de compatibilidade escrita dessa forma não tem muita utilidade para a gente.
Precisamos conseguir descrever as variações de comprimento e em função dos carregamentos nessas peças.
Mas lembra aí!
Existe uma fórmula que nos fornece essas variações de comprimento a partir do carregamento em uma peça:
(É a fórmula que vem da combinação das definições da tensão normal média e da deformação com a Lei de Hooke .)
Aplicando essa fórmula para as nossas variações de comprimento, temos que:
Nessa equação, conseguimos observar que:
- A força normal vai ser igual a menos a força de compressão no aço;
- Da mesma forma, a força normal no alumínio vai ser ;
- Tanto o núcleo de aço quanto o tubo de alumínio possuem o mesmo comprimento inicial , então os termos e vão se cortar;
- A área do núcleo de aço pode ser encontrada em função de seu diâmetro usando a fórmula ;
- E, por último, a área do tubo de alumínio é igual à área do círculo externo menos a área do círculo interno .
Fazendo todas essas operações, aquela expressão fica assim:
Multiplicando os dois lados por , temos:
O que significa que:
Substituindo os valores , , e e calculando tudo, encontramos que:
Passo 4
Agora que temos uma relação entre as incógnitas e além da relação que veio do equilíbrio de forças...
...conseguimos unir essas duas relações para encontrar os valores de e .
Substituindo na relação que veio do equilíbrio de forças, temos que:
O que significa que:
Como é igual a , encontramos que:
E, como , isso significa que:
Passo 5
Agora que conhecemos os carregamentos em cada peça, podemos calcular as tensões normais médias para cada peça.
Para o núcleo de aço, temos:
Já vimos anteriormente que e que , então temos que:
Substituindo os valores e , isso dá:
Como esse número é um pouco pequeno, podemos reescrever essa tensão em :
Já para o tubo de alumínio, temos:
No passo 3, vimos que e , então:
Substituindo , e e calculando tudo, encontramos:
E, finalmente, reescrevendo em encontramos que:
Passo 6
Resolvido o item , seguimos para o item !
No item , queremos saber a deformação do conjunto, que é a deformação sofrida tanto pelo aço quanto pelo alumínio.
Escolhendo por aplicar a Lei de Hooke para o aço, temos:
Isolando :
Substituindo e , temos que:
Calculando isso, encontramos nossa resposta:
Se quisermos, ainda podemos escrever essa resposta com uma unidade de deformação como ou .
Resposta
Exercício Resolvido #3
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 102-4.39.
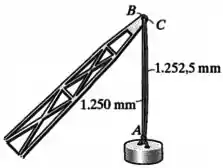
A carga de deve ser suportada pelos dois cabos verticais de aço para os quais . Se os comprimentos originais dos cabos e forem e respectivamente, determine a força desenvolvida em cada cabo depois da suspensão da carga. Cada cabo tem área de seção transversal de .
Dados: .
Passo 1
O que está acontecendo?
Os cabos e possuem comprimentos originais e , um módulo de elasticidade e uma área de seção transversal .
Através de forças de tração e , eles suportam juntos a carga de :
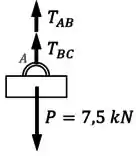
Inicialmente, os cabos têm comprimentos diferentes.
Mas uma vez que os cabos são carregados com o peso, eles:
- Sofrem variações de comprimento e ;
- E passam a compartilhar o mesmo ponto , o que significa que eles precisam ter comprimentos finais iguais.
E o que é que o exercício quer?
Ele quer saber o valor dessas forças de tração e desenvolvidas nos cabos.
Para encontrar essas duas forças, podemos recorrer ao equilíbrio de forças no ponto e a uma equação de compatibilidade entre as variações de comprimento e .
Passo 2
Vamos começar fazendo um diagrama de corpo livre do ponto :
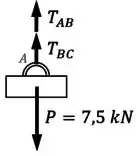
Com isso, podemos agora aplicar as condições de equilíbrio no ponto .
Para esse ponto, a única condição de equilíbrio disponível é o equilíbrio de forças na vertical:
Fazendo esse somatório de forças, temos:
O que significa que:
Essa única equação não é suficiente para que a gente possa encontrar as incógnitas e , então vamos precisar também de uma equação de compatibilidade.
Passo 3
Para encontrar uma equação de compatibilidade, precisamos pensar em como os cabos vão se deformar.
No passo 1, vimos que os dois cabos devem ter os mesmos comprimentos finais :
Isso significa que:
Passando para a esquerda e para a direita, temos:
Substituindo e , vamos encontrar que:
Essa é a nossa equação de compatibilidade.
Passo 4
Para que a equação de compatibilidade seja útil para a gente, vamos precisar descrever as variações de comprimento e em função das trações e .
Para tanto, podemos usar a fórmula:
No caso dos nossos cabos, a força interna normal vai ser sempre igual à tração , ou seja:
Dessa forma, a nossa equação de compatibilidade fica assim:
Multiplicando os dois lados por , temos que:
Isolando , encontramos:
Passo 5
Agora, podemos pegar a equação que encontramos ao final do passo 2:
E substituir a expressão que acabamos de encontrar para :
Com essa expressão, conseguimos isolar e encontrar a tração desconhecida !
Multiplicamos os dois lados por :
Passamos para o outro lado e colocamos em evidência:
E finalmente isolamos :
Substituindo:
- E
Vamos encontrar que:
Encontrado o valor de uma tração, conseguimos encontrar o valor da outra.
Para isso, pegamos novamente a equação que veio do equilíbrio de forças:
Isolamos :
E substituímos e para encontrar que:
E assim está resolvido o exercício!
Resposta
Exercício Resolvido #4
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 102-4.36.
O tubo de aço A-36 tem raio externo de e raio interno de . Se ele se ajustar exatamente entre as paredes fixas antes de ser carregado, determine a reação nas paredes quando for submetido à carga mostrada.
Dados: .
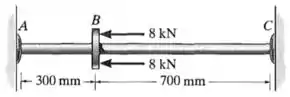
Passo 1
O que está acontecendo?
Temos um tubo de raio externo e raio interno .
Sendo assim, a área da seção transversal desse tubo vai ser dada pela diferença entre as áreas dos círculos com o raio externo e com o raio interno:
Além disso, o tubo possui um módulo de elasticidade e é dividido em dois segmentos, e , com comprimentos originais e .
Inicialmente, o tubo se ajusta exatamente nas paredes e não existe nenhuma reação nas paredes.
Mas, quando o tubo é submetido à carga mostrada, ele passa a sofrer reações das paredes em e em para que ele se mantenha em equilíbrio:
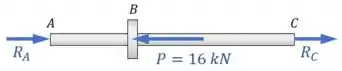
Beleza, e o que é que o exercício quer?
Ele quer saber o valor das reações desconhecidas e .
Como são duas reações desconhecidas, mas só uma condição de equilíbrio está disponível para a gente (o equilíbrio de forças na horizontal), esse tubo é estaticamente indeterminado.
Isso significa que nós vamos precisar de uma equação de compatibilidade para resolver o exercício.
Para achar essa equação de compatibilidade, podemos estudar a variação de comprimento de cada segmento do tubo.
(Também poderíamos usar o método de análise de força, mas seria mais demorado...)
Passo 2
Da mesma forma que em muitos outros exercícios, vamos começar fazendo um diagrama de corpo livre da peça:
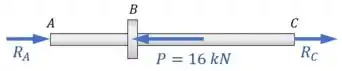
Feito o DCL, aplicamos as condições de equilíbrio.
Nesse caso, a única condição disponível é o equilíbrio de forças na vertical:
Fazendo esse somatório, encontramos que:
Vamos guardar essa equação para depois!
Passo 3
A relação não é o suficiente para encontrar os valores das reações, então precisamos de uma equação de compatibilidade.
Para encontrar essa equação, vamos observar as variações de comprimento em cada segmento da peça!
O segmento vai sofrer uma variação de comprimento enquanto que o segmento vai sofrer uma variação de comprimento .
A soma dessas duas variações vai ser a variação de comprimento total da peça:
Mas como as paredes não se movem, a variação de comprimento total da peça deve ser nula, de tal forma que:
O que significa que:
Essa é a nossa equação de compatibilidade!
Passo 4
A equação de compatibilidade da forma que encontramos no passo anterior não tem muita utilidade para a gente.
Precisamos conseguir descrever as variações de comprimento e em função dos carregamentos na peça.
Para tanto, podemos usar a fórmula:
Aplicando essa fórmula para cada segmento e tendo em mente que os dois segmentos tem módulos de elasticidade e áreas de seção transversal iguais, temos que:
Cortando com , e substituindo e , isso fica assim:
O que significa que:
Passo 5
Conseguimos relacionar os carregamentos internos nos segmentos da peça com a relação , mas precisamos mesmo é relacionar as reações na peça.
Para tanto, podemos fazer uma análise de esforços internos na peça para definir as forças internas normais em função das reações .
Para as seções entre e , temos:

Fazendo o equilíbrio de forças na horizontal, temos que:
O que significa que:
Já para as seções entre e , essa análise fica assim:

Mais uma vez aplicamos o equilíbrio de forças na horizontal:
Para encontrar dessa vez que:
Passo 6
Pronto, agora podemos voltar na relação que tínhamos encontrado:
E substituir e :
Simplificando, essa expressão fica assim:
Por fim, para resolver o exercício, precisamos substituir essa relação na Equação 1 que tínhamos guardado:
Fazendo essa substituição, temos:
Isolando , encontramos que:
O que dá:
E, como , temos que:
E assim está resolvido o nosso exercício!
Resposta
Exercício Resolvido #5
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 102-4.41.
O apoio é composto por um poste sólido de latão vermelho C83400 embutido em um tubo de aço inoxidável 304. Antes da aplicação da carga, a folga entre essas duas partes é . Dadas as dimensões mostradas na figura, determine a maior carga axial que pode ser aplicada à tampa rígida sem provocar o escoamento de qualquer um dos materiais.
Dados: , , & .
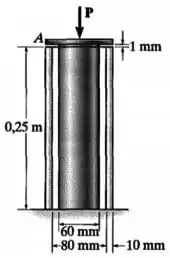
Dica do expert: Em um exercício com folga entre as peças como esse, é bom verificar se as peças vão chegar a se encostar mesmo ou não.
Passo 1
Nesse exercício, temos:
- Um poste de latão com comprimento inicial , módulo de elasticidade , e diâmetro ;
- E um tubo de aço com comprimento inicial , módulo de elasticidade , diâmetro interno e diâmetro externo .
Se o poste de latão for comprimido o suficiente pela carga , a sua face superior vai começar a se apoiar também no tubo de aço.
E o que é que o exercício quer?
Ele quer que a gente descubra a maior carga que pode ser feita sem que as tensões nos materiais ultrapassem as suas tensões de escoamento:
Agora, em um exercício com uma folga entre as peças como esse, é importante verificar se é possível fazer a folga desaparecer.
No nosso caso, precisamos verificar se a variação de comprimento de necessária para acabar com a folga já não é suficiente para fazer o poste de latão escoar.
Caso não seja, aí vamos ter a face superior do poste se apoiando no tubo de aço, e o problema vai se tornar um problema estaticamente indeterminado.
Para resolver esse problema estaticamente indeterminado, vamos ter que estudar o equilíbrio de forças nas peças e a compatibilidade das variações de comprimento de cada peça.
No nosso caso, temos que para cada milímetros de compressão no tubo de aço, o poste de latão vai ter que ter tido a mesma compressão mais a folga de .
Dessa forma, a nossa equação de compatibilidade vai ser:
Passo 2
Então, antes de podermos declarar que o exercício é estaticamente indeterminado, precisamos verificar se o latão já não vai escoar antes de encostar no tubo de aço.
Para tanto, vamos avaliar qual é a tensão no latão correspondente à variação de comprimento .
Para tanto, podemos usar a Lei de Hooke e a definição de deformação :
Juntando essas duas equações, temos que:
Para o poste de latão, isso significa que:
Sabemos que e que .
Além disso, para avaliar qual é a tensão no latão correspondente à variação de comprimento , devemos substituir .
Substituindo esses valores e calculando tudo, encontramos que:
Vemos que essa tensão é bem maior que a tensão de escoamento do latão, .
Isso significa que a carga máxima permitida no nosso conjunto vai ocorrer enquanto o latão ainda não encostou no tubo de aço.
Sendo assim, não nos precisamos nos preocupar com toda a parte estaticamente indeterminada do exercício para resolver ele!
Passo 3
Para determinar a carga máxima que pode ser aplicada no poste, vamos usar a condição:
(Ou seja, queremos que a tensão normal no latão seja menor ou igual à tensão de escoamento desse material.)
Usando a fórmula da tensão normal média para descrever a tensão no latão, a nossa condição fica assim:
Como só queremos avaliar a intensidade da tensão , não precisamos nos preocupar com o sinal da força interna normal .
Se a única força atuando no poste de latão é a força de compressão, vamos ter então que a força normal vai ter uma intensidade .
Além disso, a área da seção transversal do poste pode ser encontrada a partir do diâmetro do poste usando a fórmula:
Dessa forma, a nossa condição fica assim:
Isolando , temos que:
Substituindo os valores e , temos que:
Calculando tudo, isso nos diz que:
Ou seja, a força máxima que pode ser aplicada no poste é:
E assim está resolvido o exercício!
Caso não tivéssemos verificado se o poste ia encostar no tubo de aço, poderíamos acabar não percebendo isso depois e resolvendo o exercício de uma forma errada.
Resposta
Exercício Resolvido #6
Ferdinand P. Beer et al., Mecânica dos materiais, 5ª ed. Porto Alegre: AMGH, 2011, pp. 100-2.43.
Um tubo de aço () com diâmetro externo de e espessura de é colocado em um torno de bancada ajustado de maneira que as mandíbulas apenas toquem as extremidades do tubo sem exercerem nenhuma pressão sobre ele.
As duas forças mostradas na figura são então aplicadas ao tubo.
Após aplicar essas forças, o torno de bancada é ajustado para diminuir a distância entre suas mandíbulas em . Determine as forças aplicadas pelo torno de bancada no tubo em e e a variação do comprimento da parte do tubo.
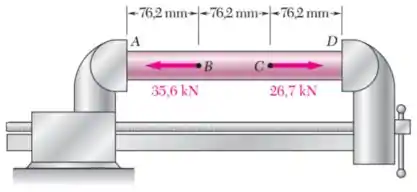
Passo 1
O tubo de aço possui um diâmetro externo e uma espessura . Dessa forma, o tubo possui um diâmetro interno .
A área da seção transversal desse tubo vai ser igual à diferença entre a área do círculo maior, de diâmetro , e a área do círculo menor, de diâmetro .
Como a área de um círculo em função de seu diâmetro é dada por , temos que:
Calculando isso, encontramos que .
Além disso, o tubo ainda tem um módulo de elasticidade e é composto por segmentos que possuem um comprimento inicial .
E o que é que está acontecendo?
Inicialmente, as mandíbulas em e em não fazem nenhuma reação no tubo.
Mas, depois que o tubo é carregado com as cargas e , as mandíbulas fazem forças de reação no tubo para mantê-lo em equilíbrio:
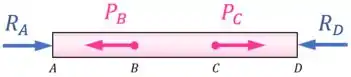
Nessa situação, o tubo é estaticamente indeterminado.
Isso porque só temos uma condição de equilíbrio disponível para usar nele (o equilíbrio de forças na horizontal), mas temos duas incógnitas (as reações e ).
Além de tudo isso, o tubo tem que, após ter sido carregado com todas as forças e reações, ter uma variação de comprimento total .
Isso porque as mandíbulas do torno foram ajustadas de forma a realizar uma compressão de no tubo.
E o que é que o exercício quer?
No item , ele quer que a gente determine as forças aplicadas pelas mandíbulas no tubo, que são as reações e .
Para determinar essas reações, vamos precisar de uma equação de equilíbrio e uma de compatibilidade.
Para encontrar a equação de compatibilidade, vamos usar o método de análise de força para podermos treinar ele.
(Se o seu professor não usa esse método, sinta-se livre para achar a equação de compatibilidade só pensando nas deformações que vão acontecer em cada segmento do tubo!)
Já no item , ele quer saber a variação de comprimento no segmento do tubo, que pode ser encontrada usando a fórmula .
Passo 2
Podemos começar o exercício usando o método de análise de força para determinar a nossa equação de compatibilidade.
Escolhendo a reação como a reação redundante, os diagramas de carregamento e reação redundante ficam assim:
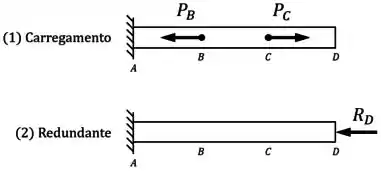
Em seguida, indicamos nesses esboços as variações de comprimento causadas por cada carregamento:
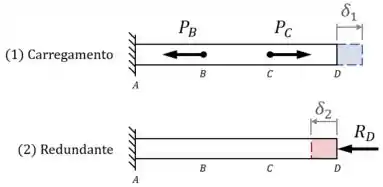
Passo 3
Agora, precisamos definir os valores das variações de comprimento e .
A variação pode ser calculada como a soma das variações em cada segmento:
Usando a fórmula e tendo em mente que os segmentos tem valores iguais para , e , essas variações ficam assim:
Olhando para o diagrama , conseguimos identificar que:
- Como o trecho está sob ação da força de tração e da força de compressão, a sua força interna normal vai ser ;
- Como o trecho só está sob a força de tração, a força interna normal vai ser ;
- E como o trecho não está sob nenhuma força, vamos ter que .
Sendo assim, a variação fica assim:
Arrumando essa expressão, encontramos que:
Já a variação vai ser a variação de comprimento causada em toda a barra pela força :
Aplicando a fórmula para essa variação de comprimento da barra na situação de carregamento do diagrama , ela fica assim:
Normalmente, a força normal na barra nessa situação seria igual à menos a força de compressão:
Mas como no método de análise de força, o sentido das deformações já é indicado nos diagramas, ignoramos esse sinal de negativo e usamos que:
E o comprimento inicial da barra é igual à soma dos comprimentos iniciais dos segmentos , e , que são todos iguais a , de tal forma que:
Sendo assim, a deformação vai ser:
Passo 4
Finalmente, podemos terminar o método de análise de força fazendo a superposição das variações de comprimento nos diagramas e .
Fazendo a superposição da variação para a direita com a variação para a esquerda, encontramos que a variação de comprimento total do tubo vai ser:
Essa é a nossa equação de compatibilidade!
Substituindo as expressões encontradas no passo anterior para e , temos que:
Essa expressão está meio poluída assim, mas se conseguirmos isolar a reação nela, vamos conseguir encontrar o seu valor!
Passo 5
Para isolar na equação anterior, começamos multiplicando os dois lados por :
Isolando , temos que:
Ou seja, vai ser dado por:
Se substituirmos nessa expressão os valores:
- ;
- ;
- ;
- ,
- ;
- E
O resultado para a força vai sair em , já que todos os valores substituídos estão em função das unidades e .
Fazendo essas substituições e calculando tudo, encontramos que:
Passo 6
Agora, para encontrar , podemos recorrer ao diagrama de corpo livre do tubo:
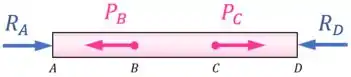
Aplicando o equilíbrio de forças na horizontal, temos que:
Fazendo esse somatório de forças:
Isolando :
Substituindo os valores de , e , temos que:
O que dá:
Os valores que encontramos e são positivos, o que significa que essas reações têm mesmo os sentidos que desenhamos.
E assim finalizamos o item !
Passo 7
No item , o exercício quer saber a variação de comprimento do trecho , .
Usando a fórmula , e tendo em mente que o trecho tem um comprimento inciial , um módulo de elasticidade e uma área de seção transversal , temos que:
Dessa forma, só nos resta descobrir qual é o valor da força interna normal no trecho .
Para tanto, podemos avaliar os esforços internos em uma seção entre os pontos e da peça:
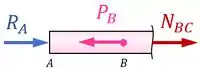
Do equilíbrio de forças na horizontal, temos:
Isolando , encontramos que:
Assim, a deformação vai ser:
Substituindo , , , e , encontramos que:
Resposta
Exercício Resolvido #7
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 104-4.51.
O conjunto é composto por um parafuso de aço A-36 e um tubo de latão vermelho C83400. Se a porca for apertada contra o tubo de modo que , e quando girada um pouco mais, avance no parafuso, determine a força no parafuso e no tubo. O parafuso tem diâmetro de e o tubo tem área de seção transversal de .
Dados: , .

Passo 1
O que está acontecendo?
Temos um parafuso de aço e um tubo de latão com módulos de elasticidade e , respectivamente.
O parafuso tem uma seção transversal com diâmetro enquanto que o tubo de latão tem uma área de seção transversal .
Inicialmente, as duas peças tem um comprimento e não estão tensionadas.
Quando a porca avança no parafuso, ela e a cabeça do parafuso comprimem o tubo de latão com uma força :

Como reação à essa compressão, o tubo de latão empurra a porca e a cabeça do parafuso de volta com forças de mesma intensidade , o que gera uma tração no parafuso:

E o que é que o exercício quer?
Ele quer que a gente encontre o valor dessa força no parafuso e no tubo.
Como a força é a única força atuando nessas peças (não temos nenhuma força externa), não adianta usar as condições de equilíbrio.
Então vamos ter que recorrer a uma equação de compatibilidade para resolver o exercício.
Passo 2
Para entender como vai ser a equação de compatibilidade nesse exercício, vamos ter que pensar no que a porca faz ao avançar no parafuso.
Pensa aí...
Se o parafuso fosse rígido (não se deformasse), a porca teria que comprimir o tubo de latão para poder avançar essa quantidade na rosca do parafuso.
Por outro lado, se o tubo de latão fosse rígido, a porca teria que esticar o parafuso para poder avançar essa quantidade na sua rosca.
Mas, no nosso caso, tanto o parafuso quanto o tubo se deformam...
Então isso significa que, somando o encurtamento do tubo e o alongamento do parafuso, a porca tem que gerar uma variação de comprimento total de nas peças.
Dessa forma, encontramos a nossa equação de compatibilidade:
Onde:
- é a intensidade do alongamento do parafuso de aço por causa da tração ;
- E é a intensidade do encurtamento do tubo de latão devido à compressão .
Passo 3
Agora que temos a nossa equação de compatibilidade, precisamos de alguma forma usar ela para encontrar o valor do carregamento nas peças.
Para tanto, podemos usar a fórmula que nos dá a variação de comprimento em função do carregamento em uma peça:
Usando isso e tendo em mente que tanto o parafuso de aço quanto o tubo de latão têm o mesmo comprimento inicial . a nossa equação de compatibilidade fica assim:
As forças internas normais de tração no parafuso de aço e de compressão no tubo de latão vão ser iguais à força nessas peças.
Além disso, a área da seção transversal do parafuso pode ser encontrada a partir de seu diâmetro usando a fórmula .
Fazendo essas substituições, temos que:
Arrumando tudo, isso fica assim:
Passo 4
Como o que queremos é encontrar o valor da força nas peças, só nos resta agora isolar na expressão que acabamos de encontrar.
Colocando em evidência, temos que:
Isolando , encontramos:
Se substituirmos nessa expressão:
- ;
- ;
- ;
- ;
- E
Vamos ter que o resultado de vai sair em , já que todos esses valores já estão em função das mesmas unidades ( e ).
Dessa forma, fazendo essas substituições e calculando tudo, encontramos nossa resposta:
Resposta
Exercício Resolvido #8
Ferdinand P. Beer et al., Mecânica dos materiais, 5ª ed. Porto Alegre: AMGH, 2011, pp. 101-2.46.
A barra rígida é suportada por quatro fios idênticos. Determine a tração em cada fio causada pela carga mostrada.
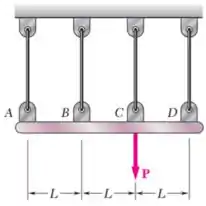
Passo 1
Temos uma barra rígida carregada com uma força e sustentada por fios igualmente espaçados por uma distância .
Fazendo o diagrama de corpo livre dessa barra, vemos que a força é equilibrada pelas forças de tração dos fios:
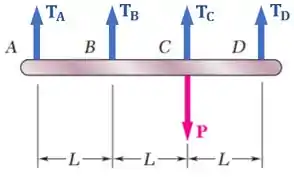
O exercício quer saber o valor dessas trações , , e .
Para fazer isso, o primeiro passo é aplicar as condições de equilíbrio na barra para tentar relacionar as forças de tração com a carga .
Mas só temos duas equações de equilíbrio que podem ser usadas aqui (o equilíbrio de forças na vertical e o equilíbrio de momentos).
Ou seja, as condições de equilíbrio não serão o suficiente para encontrar as quatro trações desconhecidas.
Para complementar as equações de equilíbrio, vamos precisar imaginar como vão ser as variações de comprimento .
Assim, vamos conseguir encontrar as equações de compatibilidade desse problema.
Passo 2
Vamos começar aplicando as condições de equilíbrio na barra !
Primeiro, podemos aplicar o equilíbrio de forças na vertical:
Fazendo esse somatório, encontramos que:
Ou seja:
Em seguida, podemos aplicar o equilíbrio de momentos.
Escolhendo avaliar os momentos em relação ao ponto , temos:
Olhando para o diagrama de corpo livre que fizemos no Passo 1, conseguimos identificar os seguintes momentos em relação ao ponto :
- Um momento no sentido horário () gerado pela tração com um braço ;
- Outro momento no sentido horário (), dessa vez gerado por e com um braço ;
- E um momento no sentido anti-horário () gerado por com um braço .
Dessa forma, o nosso somatório de momentos fica assim:
Dividindo tudo por e isolando , temos que:
Passo 3
Se temos trações desconhecidas mas somente equações de equilíbrio, precisamos encontrar equações de compatibilidade para podermos determinar todas as trações.
Para tanto, vamos imaginar como as variações de comprimento de cada fio vão afetar o posicionamento da nossa barra:
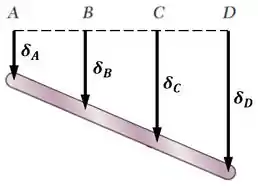
A partir dessas variações, podemos desenhar três triângulos:
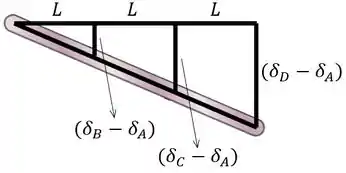
Fazendo uma semelhança de triângulos entre o triângulo menor e o triângulo médio, temos que:
Multiplicando tudo por , isso fica assim:
Isolando , encontramos a nossa primeira equação de compatibilidade:
Fazendo outra semelhança de triângulos, dessa vez entre o triângulo menor e o triângulo maior, temos que:
Multiplicando tudo por e isolando , encontramos nossa segunda equação de compatibilidade:
Passo 4
Do jeito como encontramos no passo anterior, as equações de compatibilidade e ainda não são muito úteis.
Para que elas sejam úteis, precisamos usar elas para relacionar as trações nos fios.
Então vamos pensar...
A variação de comprimento em um fio pode ser obtida pela fórmula:
Nos nossos fios, a força interna normal vai ser sempre igual à tração , ou seja:
Agora, o termo é igual para todos os fios, afinal, todos os fios são idênticos, a única coisa que muda entre eles é a tração .
Podemos dizer que esse termo é uma constante de tal forma que a relação abaixo vale para qualquer um dos nossos fios:
Sendo assim...
As equações de compatibilidade podem ser reescritas em função das trações em cada fio.
A equação pode ser reescrita assim:
O que significa que:
Da mesma forma, a equação vai significar que:
Passo 5
Agora sim temos equações relacionando as quatro trações desconhecidas , , e !
Com isso, só falta combinar essas equações para encontrar o valor individual de cada uma.
Primeiro, unindo a Equação 2 e a Equação 4, temos que:
Passando tudo para a esquerda, temos:
Isolando , encontramos que:
Vamos guardar essa relação como a Equação 5! 😊
Além disso, podemos pegar a Equação 1:
E substituir nela as Equações 2 e 3:
Arrumando isso, encontramos que:
Substituindo a Equação 5 aqui, isso fica assim:
O que significa que:
Encontrado , podemos usar a Equação 5 para encontrar :
Encontrados e , podemos usar a Equação 2 para encontrar :
E, finalmente, encontrados , e , podemos usar a Equação 1 para encontrar :
E assim está resolvido o nosso exercício!
Resposta
Exercício Resolvido #9
Elaboração própria
Determine o valor das reações causadas pela peça submetida ao carregamento mostrado abaixo. Use e considere a seção da peça quadrada com dimensões (20x20)cm.
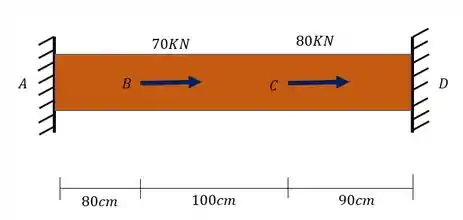
Passo 1
Como podemos ver, nesse tipo de questão precisamos determinar as reações de apoio. Para determinarmos essas reações de apoio precisamos saber se o nosso problema é isostático ou se é um problema estaticamente indeterminado. Como temos duas paredes no nosso problema, podemos desconfiar que talvez seja a segunda opção.
Para termos certeza que se trata de um problema estaticamente indeterminado, precisamos definir o diagrama de corpo livre e fazer o balanceamento entre o número de incógnitas e o número de equações, então vamos lá
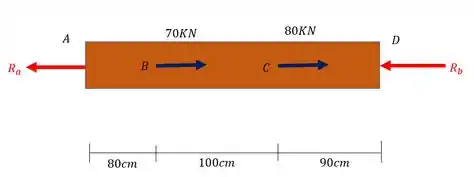
Fazendo o somatório de forças teremos que
Como podemos ver temos duas incógnitas ( e uma única equação (), logo de fato se trata de um problema estaticamente indeterminado. Sabemos então, que para resolve-lo precisamos do que chamamos de equação de compatibilidade.
Passo 2
Temos que lembrar que a nossa equação de compatibilidade terá como fórmula a nossa equação de deformação total, dada por
Mas onde ela será usada?
Ai que entra a nossa relação de deformação, ou seja, a deformação da nossa barra deve ser igual a deformação total máxima que ela pode ter, que pode ser dada por
O que precisamos saber primeiro: como as paredes são indeslocaveis a deformação total máxima possível para a nossa barra é zero, logo
O que devemos saber por segundo é que a deformação do trecho AD é composto de três parcelas, uma do trecho AB, uma do trecho BC e por fim do trecho CD. Logo podemos escrever a nossa equação de compatibilidade como.
Colocando tudo em termos do que já temos e também usando a nossa fórmula de deformação total teremos que
Sabemos que como a barra é homogênea, tanto a área quanto o módulo de elasticidade são iguais nos três trechos. Também sabemos facilmente determinar o valor de cada comprimento que é dado no desenho. Então o que falta é apenas determinar o valor dos normais.
Passo 3
Como só falta determinar o normal, basta apenas que cortemos as barras e façamos o equilíbrio da nossa peça.
Primeiro normal do trecho AB
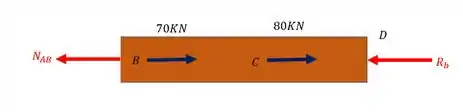
Fazendo o equilíbrio teremos que
Normal do trecho BC
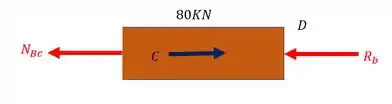
Fazendo o equilíbrio teremos que
Normal do trecho CD
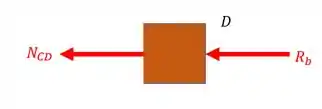
Fazendo o equilíbrio teremos que
Passo 4
Agora que já temos os valores dos normais vamos substituir na nossa equação
Agora vamos isolar os valores de
Podemos cortar
Isolando teremos que
Agora é só calcularmos o valor de
Passo 5
Sabemos que
Substituindo teremos que
Como já sabemos qual é a nossa primeira equação, basta substituir nela para descobrimos o valor de
Resposta
Exercício Resolvido #10
Elaboração própria
A barra de aço abaixo está distante 2cm da parede a sua direita. Determine as reações da parede quando a barra for submetida ao carregamento mostrado abaixo. Use e considere a área da seção como uma área quadrada de dimensões (25x25)cm.
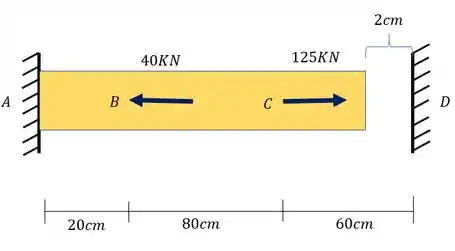
Passo 1
Como podemos ver, nesse tipo de questão precisamos determinar as reações de apoio. Para determinarmos essas reações de apoio precisamos saber se o nosso problema é isostático ou se é um problema estaticamente indeterminado. Como temos duas paredes no nosso problema, podemos desconfiar que talvez seja a segunda opção.
Para termos certeza que se trata de um problema estaticamente indeterminado, precisamos definir o diagrama de corpo livre e fazer o balanceamento entre o número de incógnitas e o número de equações, então vamos lá
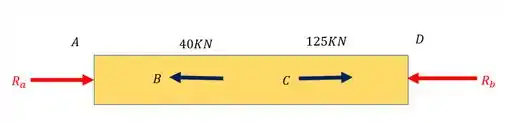
Fazendo o somatório de forças teremos que
Vamos considerar para direita positivo e para esquerda negativo, se no final a resposta tiver sinal negativo significa que a direção que escolhemos na verdade é contraria, logo teremos que
Como podemos ver temos duas incógnitas ( e uma única equação (), logo de fato se trata de um problema estaticamente indeterminado. Sabemos então, que para resolve-lo precisamos do que chamamos de equação de compatibilidade.
Passo 2
Temos que lembrar que a nossa equação de compatibilidade terá como fórmula a nossa equação de deformação total, dada por
Mas onde ela será usada?
Ai que entra a nossa relação de deformação, ou seja, a deformação da nossa barra deve ser igual a deformação total máxima que ela pode ter, que pode ser dada por
O que precisamos saber primeiro: a nossa barra sofre um deslocamento total máximo de 2cm
O que devemos saber por segundo é que a deformação do trecho AD é composto de três parcelas, uma do trecho AB, uma do trecho BC e por fim do trecho CD. Logo podemos escrever a nossa equação de compatibilidade como.
Colocando tudo em termos do que já temos e também usando a nossa fórmula de deformação total teremos que
Sabemos que como a barra é homogênea, tanto a área quanto o módulo de elasticidade são iguais nos três trechos. Também sabemos facilmente determinar o valor de cada comprimento que é dado no desenho. Então o que falta é apenas determinar o valor dos normais.
Passo 3
Como só falta determinar o normal, basta apenas que cortemos as barras e façamos o equilíbrio da nossa peça.
Primeiro normal do trecho AB

Fazendo o equilíbrio teremos que
Normal do trecho BC
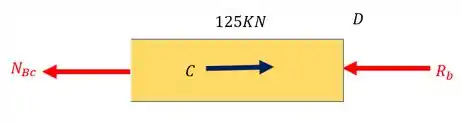
Fazendo o equilíbrio teremos que
Normal do trecho CD
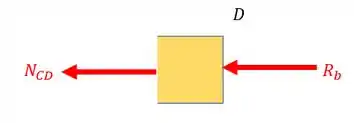
Fazendo o equilíbrio teremos que
Passo 4
Agora que já temos os valores dos normais vamos substituir na nossa equação
Agora vamos isolar os valores de
Podemos multiplicar todos os termos por
Isolando teremos que
Agora é só calcularmos o valor de
Passo 5
Sabemos que
Quando multiplicarmos EA teremos a resposta em KN
Substituindo teremos que
Como já sabemos qual é a nossa primeira equação, basta substituir nela para descobrimos o valor de