Tensões Térmicas
Produzido por Pablo RicardoTeoria
Introdução
Se você já viu os trilhos de um de trem, você pode ter percebido como existem folgas entre eles:
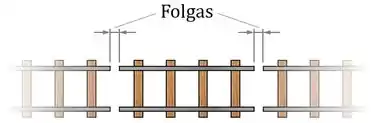
O que acontece é que o tamanho dos trilhos varia de acordo com a temperatura:
- Quando a temperatura aumenta, os trilhos se expandem;
- E quando a temperatura diminui, os trilhos se contraem.
Esse efeito é o que a gente chama de dilatação térmica.
Daí que quando os trilhos não têm folgas grandes o suficiente, esse efeito faz os trilhos se encostarem em dias muitos quentes:
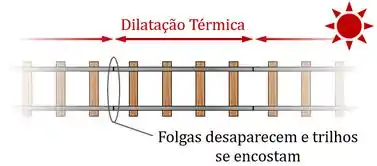
O problema disso é que qualquer aumento adicional de temperatura vai fazer com que os trilhos queiram crescer mais ainda.
Com isso, os trilhos começam a “lutar” por espaço e se comprimir, gerando nas peças uma tensão que chamamos de tensão térmica.
Então...
Como é que nós podemos calcular essas tensões?
E em que outras situações elas ocorrem?
Dilatação Térmica
Para responder essa pergunta, precisamos primeiro saber descrever a dilatação térmica que ocorre nos trilhos.
Para tanto, vamos ver cada trilho como uma barra de comprimento inicial e temperatura inicial :

Com a mudança da temperatura para uma temperatura final , os trilhos sofrem uma variação de comprimento térmica e adquirem um comprimento final :
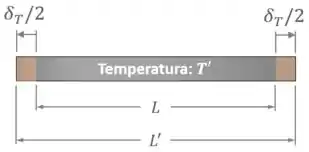
Fórmula da Dilatação Térmica
Daí que através de experimentos, foi descoberto que essa variação de comprimento em uma peça por causa de uma variação de temperatura é dada pela fórmula:
Onde:
- é uma propriedade de cada material chamada de coeficiente de dilatação linear térmica;
- E é a variação de temperatura sofrida pela peça.
Perceba que estamos analisando apenas uma dimensão dos objetos (vigas e barras por exemplo) por isso faz sentido usar o coeficiente linear de dilatação térmica .
Além disso, normalmente temos que:
- A variação de temperatura é dada em ;
- O coeficiente é dado em ou ;
- E o comprimento e a variação de comprimento são dados em uma unidade de comprimento, como ou .
Tensões Térmicas
Agora, se as barras dos nossos trilhos pudessem realmente expandir e contrair livremente como acabamos de ver, nunca seria gerada nenhuma tensão nelas, pois não haveria nenhuma força atuando sobre elas.
O problema é que os trilhos têm uma variação de comprimento máxima que eles podem sofrer antes de se encostarem. Olhe novamente a figura dos trilhos onde a próprio folga entre eles é o :
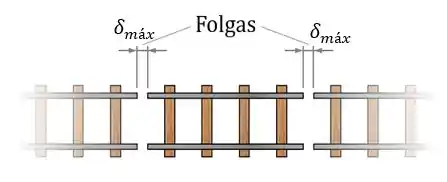
Como todos os trilhos dilatam, tanto o do meio como os da extremidade, o comprimento máximo de dilatação acaba sendo a metade da folga, ou seja:
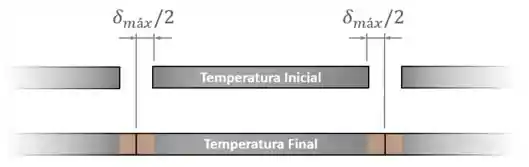
Esse limite é na verdade a própria folga entre os trilhos.
Isso significa que se a dilatação térmica sofrida por cada trilho for maior que a folga entre eles, os trilhos vão se encostar e vão passar a se comprimir com forças de reação :
![]()
São essas forças – e não a dilatação – que vão gerar as forças e tensões normais na peça. Se a gente fizer um corte transversal vamos poder ver a força normal:
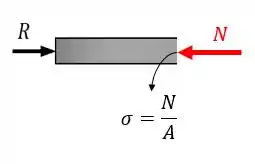
- Uma força interna normal compressiva de módulo igual a ;
- E uma tensão normal média , que podemos chamar de tensão térmica.
Mas então...
Como é que a gente faz para calcular o valor dessas reações ?
Cálculo das Reações
O primeiro passo sempre é aplicar as condições de equilíbrio na peça.
Mas como as condições de equilíbrio não vão ser suficientes para determinar as reações , vamos ter um problema estaticamente indeterminado.
Então vamos precisar de uma equação de compatibilidade, que podemos obter usando o princípio da superposição.
Basicamente, consideramos que:
- A peça vai sofrer uma dilatação térmica genérica ;
- E o carregamento na peça vai gerar nela uma variação de comprimento genérica .
Pelo princípio da superposição, a variação de comprimento total na peça vai ser a soma desses efeitos individuais:
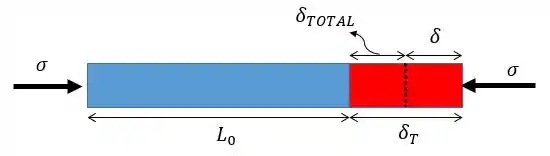
Vou explicar do ponto de vista da barra:
- “Que legal, ta tão fresquinho aqui que eu to super de boas, meu comprimento é e ninguém me incomoda!” Disse a barra.
Subitamente a temperatura aumentou muito.
- “Nossa aqui ta muito quenteee, eu preciso dilatar se não eu vou passar mal”. Pensou a barra.
E ela começou a dilatar... Até que:
- “Pera aí dona barra! Você não pode dilatar tanto assim. Você já usou todo seu espaço de dilatação, vou ter que fazer você voltar ” Explicou a tensão normal .
- “Ahh meu deus!! Que horror, eu tentei dilatar mas só consegui dilatar e ainda estou sob extrema tensão compressiva” Entendeu a senhorita barra.

A dona barra entendeu e você entendeu também? Espero que sim!!
Então se a gente souber descrever:
- A dilatação térmica ;
- A variação de comprimento devido ao carregamento na peça, normalmente dada pela fórmula ;
- E a variação de comprimento total que a peça deve ter (que no nosso caso vai ser igual à folga entre os trilhos),
Podemos usar essa equação de compatibilidade para determinar as reações na peça!
Exemplo
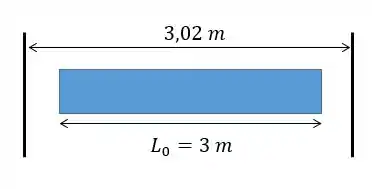
Então vamos resolver um exemplo! Imagina que a dona barrinha tem inicialmente , seu coeficiente de dilatação linear é , coeficiente de elasticidade . e área igual a . Sabendo que a dona barrinha encontra-se num vão com de comprimento. Qual será a força e a tensão normal gerada na dona barrinha se a variação de temperatura é de ?
Resolução:
A primeira coisa que a gente faz é calcular a dilatação térmica da barra:
Substituindo os valores fornecidos:
Ou seja, a barra quer expandir . Mas ela tem apenas para isso, esse é o valor do olha só!
Você pode endenter também como que é o quanto a barra de fato dilata.
Assim podemos achar o valor de :
Deu negativo e isso faz total sentido já que essa deformação comprime a barra!!
Agora é só utilizar a equação da tensão normal:
Substituindo os valores, lembrando que temos de utilizar a área em ao invés de
E a tensão é dada por:
Ambas são negativas porque a barra está sendo comprimida! E que tensão né!! provavelmente com esse valor a dona barrinha vai arrebentar coitada kkk
Duas observações finais
1. De uma forma geral, podemos afirmar que as tensões térmicas só aparecem em peças que forem estaticamente indeterminadas.
Então se você tem uma estrutura estaticamente DEterminada, a dilatação dessa estrutura (expansão ou contração) não vai afetar as tensões nela!
2. Algumas vezes, um exercício pode pedir que você calcule não a variação de comprimento térmica , mas sim a deformação térmica em uma peça. Aí é só lembrar que deformação é a variação do comprimento (no caso a dilatação) sobre o comprimento total.
Nesses casos, como deformação é definida como , vamos ter que:
O que significa que:
Tensões Térmicas
Exemplo
Duas observações finais
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
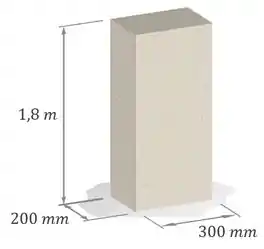
A coluna de concreto abaixo tem, a uma temperatura de , um comprimento inicial . Determine o comprimento final dessa coluna quando a temperatura é abaixada para .
Dados:
Passo 1
O que está acontecendo?
A coluna possui um comprimento inicial , uma temperatura inicial e um coeficiente de dilatação térmica .
Ao ter a sua temperatura abaixada até uma temperatura final , a coluna sofre uma variação de comprimento térmica que vai ser dada pela fórmula
Onde é a variação de temperatura sofrida pela coluna, de tal forma que:
E o que é que o exercício quer?
Ele quer saber o comprimento final dessa coluna.
Como o comprimento final é o comprimento final mais a variação de comprimento, vamos ter que:
Substituindo , temos que:
Colocando em evidência, isso fica assim:
Passo 2
Encontrada uma expressão para em função de valores conhecidos:
Podemos substituir esses valores para encontrar .
Substituindo:
- ;
- ;
- ;
- E ;
Vamos ter que:
Calculando tudo, encontramos a nossa resposta:
Resposta
Exercício Resolvido #2
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 109-4.70.
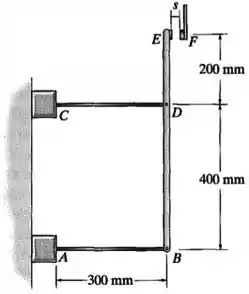
A chave elétrica fecha quando as hastes de ligação e se aquecem, o que provoca a translação e a rotação do braço rígido até fechar o contato em . A posição original de é vertical e a temperatura é . Se for feita de bronze C86100 e , de alumínio 6061-T6, determine o espaço exigido entre os contatos para a chave fechar quando a temperatura alcançar .
Dados: , .
Passo 1
O que está acontecendo?
As hastes e , ambas de comprimento inicial , possuem uma temperatura inicial .
Ao serem submetidas a uma variação de temperatura , as barras sofrem uma variação de comprimento térmica que é dada pela fórmula:
Mas as hastes e possuem coeficientes de dilatação térmica diferentes:
- A haste é feita de um bronze para o qual ;
- E a haste é feita de um alumínio para o qual ,
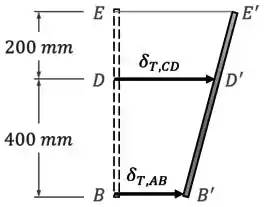
Por causa disso, cada haste vai sofrer uma dilatação térmica diferente, o que vai fazer com que o braço rígido ande para a frente e se incline:
E o que é que o exercício quer?
Ele quer saber qual é a distância entre os pontos e para que eles se encostem quando as hastes e forem aquecidas até uma temperatura final .
Para tanto, teremos que encontrar as dilatações térmicas e em cada haste.
Feito isso, desenharemos a configuração final da barra rígida após a variação de temperatura nas hastes.
Com isso, vamos conseguir avaliar qual deve ser o valor da distância para que a posição final do ponto , o ponto , coincida com o ponto .
Passo 2
Então vamos começar o exercício calculando as dilatações térmicas em cada haste.
Calculando a dilatação térmica da haste , que é de bronze, temos:
Substituindo:
- ;
- ;
- E ,
Vamos encontrar que:
Já a dilatação térmica da haste , que é de alumínio, vai ser:
Substituindo nessa expressão:
- ;
- ;
- E ,
Encontramos que:
Passo 3
O próximo passo é avaliar como vai ficar a barra rígida depois que as hastes tiverem dilatado.
Então vamos pensar...
Sabemos que a barra vai se movimentar como imaginamos na figura do passo 1, já que a dilatação da barra é maior.
E o que é que queremos...
Queremos que a posição final do ponto coincida com o ponto para que a chave elétrica feche.
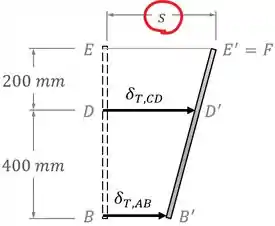
Então vamos ter que o deslocamento do ponto da barra tem que ser igual à distância inicial entre os pontos e :
Passo 4
Finalmente, podemos tentar encontrar o valor da distância .
Para tanto, precisamos observar os triângulos formados pela barra em sua posição final:
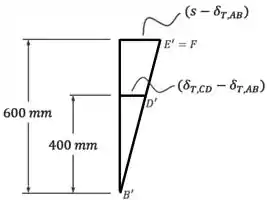
Fazendo uma semelhança de triângulos entre o triângulo menor e o triângulo maior, vamos ter que:
Simplificando os termos que estão dividindo, isso fica assim:
Isolando , temos:
Em seguida, isolando a distância , encontramos:
Finalmente, fazendo a distributiva e simplificando tudo, encontramos que:
Com isso, só falta substituir os valores das dilatações térmicas para encontrarmos o valor da distância !
Substituindo e , vamos ter que:
O que dá a nossa resposta:
Resposta
Exercício Resolvido #3
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 109-4.73.
Uma placa de concreto de alta resistência utilizada em uma pista de rolamento tem de comprimento quando sua temperatura é . Se houver uma folga de em um de seus lados antes de tocar seu apoio fixo, determine a temperatura exigida para fechar a folga. Qual é a tensão de compressão no concreto se a temperatura aumentar até ?
Dados: , .
Passo 1
O que está acontecendo?
A placa de concreto:
- Tem um comprimento inicial quando ela está submetida a uma temperatura inicial ;
- E possui um coeficiente de dilatação térmica e um módulo de elasticidade .
Além disso, a placa tem uma folga antes de encostar em seu apoio fixo em um dos seus lados:

Agora, se a temperatura dessa placa variar até uma temperatura final , ela vai sofrer uma dilatação térmica dada pela fórmula:
Onde é a variação de temperatura na placa.
Se essa dilatação térmica for maior que a folga , a placa vai passar a ser restringida pelos apoios em suas extremidades, que vão realizar forças de reação nela:

Esse carregamento gera na placa uma variação de comprimento .
Pelo princípio da superposição, a variação de comprimento total na placa vai ser igual à soma da dilatação térmica com essa variação de comprimento :
Como ao fechar a folga , a placa passa a ser impedida de continuar variando o seu comprimento, ainda vamos ter que:
E o que é que o exercício quer saber?
Primeiro, ele quer que a gente encontre a temperatura final exigida para que a dilatação térmica seja igual à folga .
Em seguida, ele quer saber qual vai ser a tensão normal de compressão causada pelas reações na placa quando a temperatura final for .
Não conhecemos a área da seção transversal da placa para podermos usar a fórmula da tensão normal média .
Então vamos ter que usar a Lei de Hooke para calcular a tensão , usando que e que .
Passo 2
Então primeiro, vamos calcular qual é a temperatura final para que seja igual a folga .
Da fórmula para , temos que:
Agora vamos pensar...
Nessa expressão, podemos substituir por .
Além disso, queremos saber qual é o valor de para que , então podemos substituir por .
Fazendo essas substituições, nossa expressão fica assim:
Com isso, podemos isolar para encontrar que:
Substituindo nessa expressão os valores:
- ;
- ;
- ;
- & ,
E calculando tudo, encontramos o resultado para a primeira parte do exercício:
Passo 3
Na segunda parte, o exercício quer saber qual é a tensão na placa quando a temperatura final é .
Como vimos no passo 1, vamos ter que usar a Lei de Hooke para calcular essa tensão :
Como o módulo de elasticidade da placa é , temos que .
Além disso, a deformação é definida como .
Substituindo esses valores, a Lei de Hooke fica assim:
Conhecemos os valores de e de , mas precisamos descobrir o valor da variação de comprimento devido ao carregamento na peça.
Passo 4
Para descobrir o valor de , podemos recorrer à equação de compatibilidade que obtivemos através do princípio da superposição no Passo 1:
Isolando , temos que:
Aqui, sabemos que a variação de comprimento total máxima que a placa pode sofrer é igual à folga .
E sabemos que .
Dessa forma, temos que:
Passo 5
Substituindo essa expressão que acabamos de encontrar para na expressão que encontramos no Passo 3 para a tensão , temos:
Simplificando, isso fica assim:
Finalmente, substituindo nessa expressão os valores:
- ;
- ;
- ;
- ;
- &
Encontramos o nosso resultado para a segunda parte do exercício:
Nesse resultado, o sinal de negativo () indica que essa é uma tensão de compressão.
Como o exercício já afirma que ele quer saber a “tensão normal de compressão”, podemos retirar esse sinal e fornecer o resultado como:
E assim está terminado o exercício!
Resposta
Exercício Resolvido #4
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 123-4.114.
A haste de alumínio 2014-T6 tem diâmetro de e está levemente conectada aos apoios rígidos em e quando . Se a temperatura baixar para e uma força axial for aplicada ao colar rígido, como mostra a figura, determine as reações em e .
Dados: , .
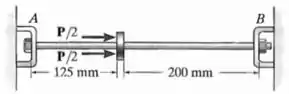
Passo 1
O que sabemos sobre a haste?
A haste tem um comprimento inicial .
Ela é dividida pelo colar rígido (que podemos chamar de “”) em dois segmentos de comprimentos iniciais e .
Além disso, ela tem um diâmetro , módulo de elasticidade , coeficiente de dilatação térmica e uma temperatura inicial .
E ela está levemente conectada aos apoios rígidos em e , ou seja, os apoios não realizam nenhuma força significativa na haste.
E o que é que está acontecendo?
Quando a temperatura é abaixada para , a haste sofre uma variação de temperatura .
Por causa dessa variação de temperatura, ela sofre uma contração térmica :
Mas os em e em são fixos.
Então eles vão aplicar na haste reações e com as intensidades que forem necessárias para que a variação de comprimento total na haste seja nula:
E, em seguida, ainda é aplicado na haste a carga axial no ponto .
Dessa forma, o diagrama de corpo livre da haste fica assim:
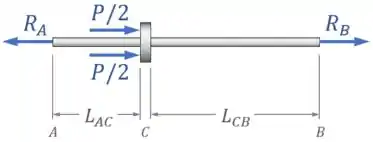
Essas cargas vão gerar nos segmentos e forças internas normais e .
Essas forças normais, por sua vez, vão gerar variações de comprimento nos segmentos e .
Daí que pelo princípio da superposição, vamos ter que a variação de comprimento total na haste vai ser a soma:
- Da dilatação térmica ;
- Da variação de comprimento do segmento , ;
- E da variação de comprimento do segmento , ;
Ou seja:
E o que é que o exercício quer?
Ele quer saber qual vai ser o valor das reações e .
Para encontrar o valor dessas reações, podemos aplicar uma equação de equilíbrio na haste para relacionar as reações com a força .
Mas isso não vai ser o suficiente para encontrar as duas incógnitas e .
Então também vamos ter que desenvolver a equação de compatibilidade para podermos relacionar e de alguma outra forma.
Passo 2
Então vamos começar fazendo o diagrama de corpo livre da haste para, em seguida, aplicarmos as condições de equilíbrio nela:
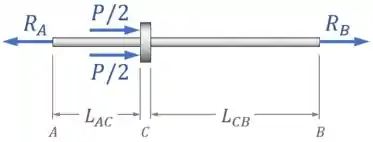
Aqui, a única condição que temos disponível é o somatório de forças na horizontal:
Fazendo esse somatório, vamos ter que:
O que significa que:
Infelizmente, essa relação não é suficiente para que a gente possa encontrar e .
Então vamos guardar ela por enquanto e seguir para o próximo passo, que é desenvolver a nossa equação de compatibilidade.
Passo 3
Para desenvolvermos os termos e da equação de compatibilidade, temos que conhecer:
- Os valores das forças normais nos segmentos e ;
- E o valor da área da seção transversal da haste.
Para encontrar o valor das forças , vamos fazer uma análise dos esforços internos na haste:
Para seções entre e , essa análise fica assim:

Pelo equilíbrio de forças, temos que:
E para as seções entre e , fica assim:

E o equilíbrio de forças nos mostra que:
Já quanto a área da seção transversal da haste, sabemos que ela é uma área circular de diâmetro .
Então podemos aplicar a fórmula da área do círculo em função de seu diâmetro:
E substituir para encontrarmos que:
Passo 4
Agora sim podemos desenvolver a nossa equação de compatibilidade:
Nessa equação, podemos desenvolver a dilatação térmica usando a sua fórmula, que vai ficas assim para a nossa haste de alumínio:
E podemos desenvolver as variações de comprimento e devido aos carregamentos em cada segmento da haste usando a fórmula .
Aplicando essa fórmula para cada um dos dois segmentos, temos:
E como e , ainda podemos dizer que:
Dessa forma, a nossa equação de compatibilidade pode ser reescrita assim:
E pronto!
Agora podemos combinar as Equações 1 e 2 para encontrarmos os valores de e !
Passo 5
Substituindo a Equação 1 () na Equação 2, temos que:
Aqui, se conseguirmos isolar nessa equação, vamos conseguir encontrar o seu valor.
Para isolar , podemos primeiro passar para o outro lado e colocar em evidência:
Em seguida, passamos para o outro lado e desenvolvemos o lado esquerdo:
E depois, passamos para o outro lado e colocamos em evidência:
Por fim, conseguimos isolar e encontrar que:
Se quisermos, ainda podemos perceber que a soma dos comprimentos dos dois segmentos da haste é o mesmo que o comprimento total da haste.
Dessa forma, a expressão para fica assim:
E ainda pode ser simplificada para ficar assim:
Substituindo os valores...
- ;
- ;
- & ,
...vamos encontrar que o termo vale:
Já substituindo...
- ;
- ;
- & ,
...vamos encontrar que vale:
Sendo assim, vai ser:
Encontrado , podemos voltar na Equação 1:
E substituir e para encontramos que:
E assim terminamos o exercício! 🎉
Resposta
Exercício Resolvido #5
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 110-4.79.
Duas barras feitas de materiais diferentes são acopladas e instaladas entre duas paredes quando a temperatura é . Determine a força exercida nos apoios (rígidos) quando a temperatura for . As propriedades dos materiais e as áreas de seção transversal de cada barra são dadas na figura.
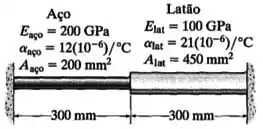
Passo 1
O que está acontecendo?
Quando as barras de aço e de latão foram instaladas a uma temperatura inicial , elas não estavam nem sob compressão nem sob tração.
Além disso, elas têm:
- Comprimentos iniciais ;
- Módulos de Elasticidade e ;
- Coeficientes de Dilatação Térmica e ;
- E áreas de seção transversal e .
Quando a temperatura é elevada para , as barras sofrem uma variação de temperatura .
Por causa dessa variação de temperatura, cada barra sofre uma dilatação térmica :
Mas as barras estão restringidas entre duas paredes fixas, que não podem ser afastadas ou aproximadas.
Então a variação de comprimento total das duas barras deve ser nula:
Para garantir que isso ocorra, o que as paredes fazem é aplicar forças de reação nas barras, comprimindo-as de forma a anular as dilatações térmicas :
![]()
Essas forças de compressão geram uma força interna normal e uma variação de comprimento em cada barra.
E o que é que o exercício quer?
Ele quer que a gente descubra o valor da força que as barras aplicam nas paredes.
Pelo princípio da ação e reação, essa força vai ser igual à força que as paredes aplicam nas barras.
(Ou seja, o exercício quer descobrir o valor de !)
Para encontrar , vamos ter que desenvolver a equação de compatibilidade...
...até que ela seja descrita em função de .
Passo 2
Para desenvolver a equação de compatibilidade , podemos começar aplicando o princípio da superposição.
Com ele, podemos descrever essa variação de comprimento total das duas barras como a soma:
- Das variações individuais e causadas pela variação de temperatura em cada barra;
- Com as variações individuais e causadas pelas forças atuantes nas barras.
Dessa forma, temos que:
Vamos guardar essa equação.
Passo 3
Agora, podemos usar a fórmula da dilatação térmica para definirmos e :
E podemos usar a fórmula da variação de comprimento devido ao carregamento em uma peça para definirmos e :
E ainda vimos no Passo 1 que a força interna normal nas barras é igual à , de tal forma que:
Daí que substituindo essas fórmulas naquela expressão que tínhamos guardado ao final do passo anterior, ela fica assim:
Dividindo tudo por , conseguimos simplificar essa expressão:
Assim, conseguimos fazer o que queríamos que era desenvolver a equação de compatibilidade até que ela fosse descrita em função da força desconhecida.
Com isso, só nos falta isolar para encontrarmos o seu valor.
Passo 4
Para isolar na expressão anterior, começamos colocando e em evidência:
Passamos o termo com para o outro lado:
E finalmente isolamos encontrando que:
Se substituirmos:
- ;
- e ;
- e ;
- & e ,
Todos os valores vão estão em função das unidades , e . Então o nosso resultado para a força vai sair em .
Fazendo essas substituições e calculando tudo, encontramos nossa resposta:
Resposta
Exercício Resolvido #6
Elaboração Própria
Na coluna de concreto reforçada com vigas de aço abaixo, tanto o concreto quanto o aço estão fixados entre o solo e uma placa rígida.
A coluna possui um comprimento inicial . Além disso, o concreto e o aço possuem módulos de elasticidade e e áreas de seção transversal e .
Considerando que não existe nenhuma carga externa na coluna e que os materiais possuem coeficientes de dilatação térmica distintos , determine a força que a placa rígida fixa faz no concreto quando a coluna for submetida a uma variação de temperatura , fazendo o concreto e o aço sofrerem dilatações térmicas distintas e .
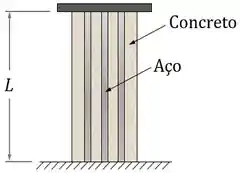
Dica do Expert: A placa rígida que fixa as extremidades do concreto e do aço vai forçar com que as variações de comprimento total dos dois materiais sejam iguais.
Passo 1
O que está acontecendo?
Se não fosse pela placa rígida, se o concreto e o aço estivessem livres um do outro, cada um sofreria as suas dilatações térmicas livremente:
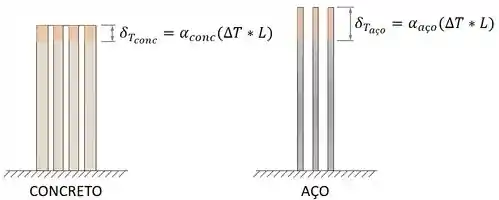
Mas, por causa da placa rígida, os materiais são forçados a ter a mesma variação de comprimento total:
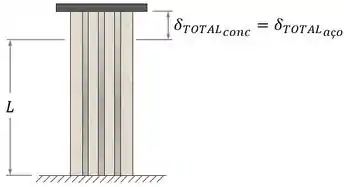
Para que isso seja possível, o que acontece é que a placa rígida fixa exerce forças no concreto e no aço, e .
Esse carregamento gera forças internas normais e nos materiais, que, por sua vez, geram neles variações de comprimento e dadas pela fórmula:
Daí que essas variações de comprimento e devido ao carregamento nas peças se encarregam de compensar a diferença entre as dilatações térmicas e .
E o que é que o exercício quer?
Ele quer saber o valor da força que a placa rígida faz no concreto.
Para encontrar essa força, provavelmente vamos precisar tanto de uma equação de equilíbrio quanto de uma equação de compatibilidade.
Passo 2
A primeira coisa que podemos fazer para encontrar uma força é fazer o diagrama de corpo livre das pelas e aplicar as condições de equilíbrio nessas peças.
Fazendo esse diagrama de corpo livre para as nossas peças, ele fica assim:
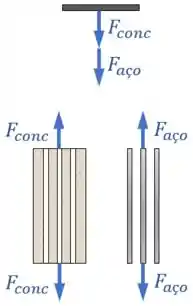
Como não sabemos ainda as direções das forças e , desenhamos ela com uma direção qualquer.
Aplicando o equilíbrio de forças na vertical para a placa rígida, temos que:
O que significa que:
Infelizmente, além disso, não tem mais nada que conseguimos extrair das equações de equilíbrio.
Então uma solução agora é encontrar uma equação de compatibilidade que nos permita relacionar as forças e de uma outra forma.
Passo 3
A verdade é que lá no Passo 1 a gente já viu uma equação de compatibilidade.
Vimos lá que, por causa da placa rígida, as variações de comprimento totais do concreto e do aço devem ser iguais:
Mas para usar essa equação de compatibilidade, precisamos desenvolver ela.
Primeiro, podemos pensar em como a variação de comprimento total em uma peça é a superposição das variações de comprimento devido à cada efeito que existe naquela peça.
No nosso caso, temos:
- Os efeitos térmicos, que geram uma dilatação térmica ;
- E os efeitos mecânicos (devido às forças na peça), que geram uma variação de comprimento .
Então a nossa equação de compatibilidade pode ser reescrita assim:
Se aplicarmos as fórmulas de e para o concreto e para o aço, isso fica assim:
Aqui, podemos observar duas coisas:
- Primeiro que como desenhamos no passo anterior as forças e como forças de tração, as forças internas normais vão ser e ;
- E segundo que podemos cortar em todos os termos dessa expressão acima.
Dessa forma, a expressão fica assim:
E pronto! Agora já temos duas equações diferentes relacionando e , o que é o suficiente para que a gente possa calcular essas forças.
Passo 4
Para encontrar , podemos substituir da equação 1 na equação 2.
Fazendo isso, temos que:
Colocando todos os termos com à esquerda e os demais à direita, temos:
Colocando e em evidência:
Daí que, finalmente, isolando , encontramos nossa resposta:
Resposta
Exercício Resolvido #7
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 110-4.81.
A haste central do conjunto é aquecida de até por resistência elétrica. As duas hastes e situadas nas extremidades também são aquecidas de até . Na temperatura mais baixa, , a folga entre e a barra rígida é . Determine a força nas hastes e provocada pelo aumento na temperatura. As hastes e são feitas de aço e cada uma tem área de seção transversal de . é feita de alumínio e tem área de seção transversal de .
Dados: , , e .
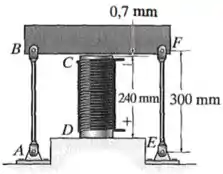
Passo 1
O que está acontecendo?
A haste central de alumínio tem:
- Um comprimento inicial ;
- Um coeficiente de dilatação térmica ;
- Uma área de seção transversal ;
- Um módulo de elasticidade ,
& vai sofrer uma variação de temperatura .
Por outro lado, para as hastes laterais de aço e , vamos ter que:
- ;
- ;
- ;
- ;
- & .
Dessa forma, essas hastes vão sofrer dilatações térmicas que vão ser dadas pela fórmula:
Mas essas hastes não podem se dilatar livremente devido a existência da barra rígida que elas suportam.
Por causa dessa barra, as hastes têm que se dilatar de tal forma que:
- O deslocamento do ponto central da barra rígida (igual à variação de comprimento total da haste central de alumínio menos a folga )...
- ...seja igual ao deslocamento dos pontos laterais da barra rígida (igual à variação de comprimento total das hastes laterais de aço).
Ou seja:
Mas a variação de comprimento total de uma haste é a soma entre a dilatação térmica e a variação de comprimento causada pelo carregamento na haste.
Dessa forma, a expressão acima pode ser reescrita assim:
(Essa é a equação de compatibilidade desse sistema!)
E como vai ser o carregamento nas hastes?
Bom...
Como é quase o dobro de , podemos imaginar que a haste central de alumínio vai se dilatar muito mais que as hastes laterais e de aço.
Então vamos ter a haste empurrando a barra rígida para cima com uma força enquanto que e puxam a barra para baixo com forças e :
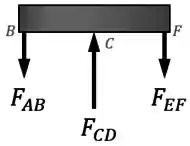
Como uma reação às forças e para baixo, a barra rígida vai puxar as hastes e para cima com forças de mesma intensidade, tracionando elas.
Já como uma reação à força para cima, a barra rígida vai empurrar a haste para baixo com uma força de mesmo intensidade, comprimindo ela.
São essas forças de tração e compressão que vão gerar as variações de comprimento e devido ao carregamento nas hastes, de acordo com a fórmula:
Onde é a força interna normal em cada haste.
E o que é que o exercício quer?
Ele quer que a gente encontre o valor das forças e .
Para encontrar essas forças, vamos ter que:
- Aplicar as condições de equilíbrio no diagrama de corpo livre da barra rígida que fizemos acima;
- & desenvolver a equação de compatibilidade que encontramos;
Com isso, vamos ter equações o suficiente relacionando os valores de , e para que a gente possa calcular essas forças! 💃
Passo 2
Então vamos começar fazendo o diagrama de corpo livre da barra ...
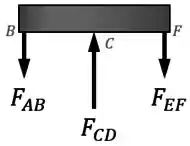
...e aplicando as condições de equilíbrio nessa barra!
Temos duas condições disponíveis aqui: o equilíbrio de forças na vertical e o equilíbrio de momentos em relação a um ponto.
Começando pelo equilíbrio de momentos em relação a um ponto, vamos escolher o ponto central :
Se a gente chamar de a distância entre o ponto central e as extremidades e , esse somatório de momentos fica assim:
O que significa que:
Já para o equilíbrio de forças na vertical, temos:
Fazendo esse somatório, encontramos que:
Isolando , temos:
Mas como acabamos de encontrar que , isso significa que:
Passo 3
Em seguida, vamos desenvolver nossa equação de compatibilidade.
Como vimos no Passo 1, temos que:
Nessa equação, podemos desenvolver as dilatações térmicas usando a fórmula:
Aplicando essa fórmula para a barra de alumínio e para as barras de aço, vamos ter que:
E podemos desenvolver as variações de comprimento devido ao carregamento nas peças usando a fórmula:
No nosso caso, temos que a força interna normal vai ser:
- E igual à para a haste central de alumínio que vai estar sob compressão.
- Igual à para as hastes laterais de aço que vão estar sob tração;
Então as variações para cada material vão ser:
Substituindo tuuuudo isso na nossa equação de compatibilidade, ela fica assim:
Eita!
Mas pensa aí... 🤔
Já temos o que precisamos para resolver o exercício:
- Queremos encontrar o valor da força ;
- E já temos duas equações (as equações 2 e 3) que relacionam as forças e , então podemos combinar essas equações para encontrar essas forças!
Passo 4
Então vamos substituir a equação 2 () na equação 3 que acabamos de encontrar no passo anterior.
Fazendo isso, vamos ter que:
Com isso, o nosso último objetivo é isolar nessa expressão!
Deixando todos os termos com de um lado e os demais termos do outro, essa expressão fica assim:
Colocando em evidência, temos que:
O que significa que:
Por fim, se substituirmos nessa expressão os seguintes valores...
- e ;
- e ;
- , e ;
- e ;
- & e ,
...e lembrarmos que é o mesmo que , vamos ter que todas as unidades vão estar em função de , e .
Então o resultado para a força nessa expressão vai sair em .
Substituindo tudo e calculando , que é igual à , vamos encontrar a nossa resposta:
Resposta
Exercício Resolvido #8
Elaboração própria
Os prédios em Dubai sofrem grandes problemas com relação as altas temperaturas durante o dia e as baixas temperaturas durante a noite. Para resolver alguns problemas relacionados a isso, em algumas ligações feitas com parafusos e porcas utiliza-se peças acopladas que se movimentem de acordo com movimentos predeterminados para estrutura. Da mesma forma, em linhas férreas podemos notar que as barras não são fixadas juntas, sempre possuindo uma pequena distancia entre trilhos sucessivos. Qual a necessidade de garantir um limitado movimento aos parafusos, assim como a distância ente trilhos.
Passo 1
Primeiro falando com relação aos parafusos. Os principais problemas que podemos encontrar estão em duas áreas. O primeiro problema está na fadiga do parafuso, em Dubai as altas temperaturas durante o dia e as baixas temperaturas durante a noite fazem com que os parafusos sofram mudanças que podem fazer que com o tempo os mesmos rompam pela fadiga. Outro problema está relacionado as tensões térmicas que apareceram tanto na dilatação quanto na contração do parafuso, essas tensões se não forem previstas, podem causar rompimento da nossa peça. Para evitar esses problemas fazemos o acoplamento de porcas e parafusos com peças que permitem certas movimentações, principalmente movimentações devido a ação da temperatura, isso é importante por garantir que as tensões térmicas sejam minimizadas e até mesmo anuladas devido a movimentação do acoplamento, essa movimentação impede que ocorram tensões provenientes da dilatação e contração dos parafusos, da mesma forma, a fadiga causada pela resistência ao movimento é minimizada, isso garante maior sobrevida e durabilidade da peça.
Passo 2
Da mesma forma os pequenos espaços entre trilhos possuem a mesma função das peças acopladas, deseja-se garantir a minimização dos efeitos causados pelas tensões térmicas, na imagem abaixo podemos ver um problema causado pela falta de previsão dessas tensões

Falhas como essas podem causar acidentes e descarrilamento do vagão dos trens.

Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #9
Elaboração própria
A barra de aço abaixo foi sujeita ao carregamento indicado. Sabendo que além disso essa barra também sofreu uma variação de temperatura de 40°C, determine qual será o valor das reações da parede para essa peça.
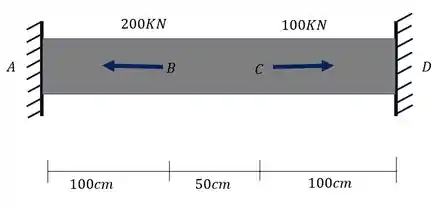
Passo 1
Como podemos ver precisamos analisar duas coisas, a primeira sabemos de cara pelo enunciado, teremos deformações térmicas e tensões térmicas.
Sabemos que podemos calcular as nossas deformações térmicas pela fórmula
E essa fórmula entrará na nossa deformação total máxima.
Além disso também devemos ver se temos um problema estaticamente indeterminado.
Para termos certeza que se trata de um problema estaticamente indeterminado, precisamos definir o diagrama de corpo livre e fazer o balanceamento entre o número de incógnitas e o número de equações, então vamos lá

Fazendo o somatório de forças teremos que
Como podemos ver temos duas incógnitas ( e uma única equação (), logo de fato se trata de um problema estaticamente indeterminado. Sabemos então, que para resolve-lo precisamos do que chamamos de equação de compatibilidade.
Passo 2
Temos que lembrar que a nossa equação de compatibilidade terá como fórmula a nossa equação de deformação total, dada por
Mas onde ela será usada?
Ai que entra a nossa relação de deformação, ou seja, a deformação da nossa barra deve ser igual a deformação total máxima que ela pode ter, que pode ser dada por
O que precisamos saber primeiro: como as paredes são indeslocaveis a deformação total máxima possível para a nossa barra é zero, logo
O que devemos saber por segundo é que a deformação do trecho AD é composto de quatro parcelas, uma do trecho AB, uma do trecho BC, uma do trecho CD e por fim uma parcela da deformação térmica . Logo podemos escrever a nossa equação de compatibilidade como.
Colocando tudo em termos do que já temos e também usando a nossa fórmula de deformação total teremos que
Sabemos que como a barra é homogênea, tanto a área quanto o módulo de elasticidade são iguais nos três trechos. Também sabemos facilmente determinar o valor de cada comprimento que é dado no desenho. Por fim sabemos quanto vale a variação de temperatura e o coeficiente de deformação térmica. Então o que falta é apenas determinar o valor dos normais.
Passo 3
Como só falta determinar o normal, basta apenas que cortemos as barras e façamos o equilíbrio da nossa peça.
Primeiro normal do trecho AB
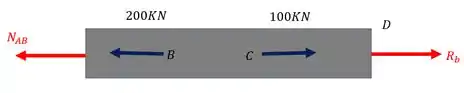
Fazendo o equilíbrio teremos que
Normal do trecho BC

Fazendo o equilíbrio teremos que
Normal do trecho CD
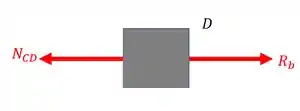
Fazendo o equilíbrio teremos que
Passo 4
Agora que já temos os valores dos normais vamos substituir na nossa equação
Agora vamos isolar os valores de
Podemos multiplicar tudo por EA
Isolando teremos que
Agora é só calcularmos o valor de
Passo 5
Sabemos que
Substituindo teremos que
Como já sabemos qual é a nossa primeira equação, basta substituir nela para descobrimos o valor de
Resposta
Exercício Resolvido #10
Elaboração própria
A barra abaixo foi submetida a uma variação de temperatura de 38°C, sabendo que ela está exatamente encaixada no vão entre as paredes, determine a reação das paredes nessa situação.

Passo 1
Como podemos ver precisamos analisar duas coisas, a primeira sabemos de cara pelo enunciado, teremos deformações térmicas e tensões térmicas.
Sabemos que podemos calcular as nossas deformações térmicas pela fórmula
E essa fórmula entrará na nossa deformação total máxima.
Além disso também devemos ver se temos um problema estaticamente indeterminado.
Para termos certeza que se trata de um problema estaticamente indeterminado, precisamos definir o diagrama de corpo livre e fazer o balanceamento entre o número de incógnitas e o número de equações, então vamos lá

Fazendo o somatório de forças teremos que
Como podemos ver temos duas incógnitas ( e uma única equação (), logo de fato se trata de um problema estaticamente indeterminado. Sabemos então, que para resolve-lo precisamos do que chamamos de equação de compatibilidade.
Passo 2
Temos que lembrar que a nossa equação de compatibilidade terá como fórmula a nossa equação de deformação total, dada por
Mas onde ela será usada?
Ai que entra a nossa relação de deformação, ou seja, a deformação da nossa barra deve ser igual a deformação total máxima que ela pode ter, que pode ser dada por
O que precisamos saber primeiro: como as paredes são indeslocaveis a deformação total máxima possível para a nossa barra é zero, logo
O que devemos saber por segundo é que a deformação do trecho AD é composto de quatro parcelas, uma do trecho AB, uma do trecho BC, uma do trecho CD e por fim uma parcela da deformação térmica . Logo podemos escrever a nossa equação de compatibilidade como.
Colocando tudo em termos do que já temos e também usando a nossa fórmula de deformação total teremos que
Sabemos que como a barra é homogênea, tanto a área quanto o módulo de elasticidade são iguais nos três trechos. Também sabemos facilmente determinar o valor de cada comprimento que é dado no desenho. Por fim sabemos quanto vale a variação de temperatura e o coeficiente de deformação térmica. Então o que falta é apenas determinar o valor dos normais.
Passo 3
Como só falta determinar o normal, basta apenas que cortemos as barras e façamos o equilíbrio da nossa peça.
Normal do trecho AB

Fazendo o equilíbrio teremos que
Passo 4
Agora que já temos os valores dos normais vamos substituir na nossa equação
Agora vamos isolar os valores de
Podemos multiplicar tudo por EA
Isolando teremos que
Agora é só calcularmos o valor de
Passo 5
Sabemos que
Substituindo teremos que
Como já sabemos qual é a nossa primeira equação, basta substituir nela para descobrimos o valor de