Calcule a integral de linha de
ao longo do caminho fechado que é fronteira da região entre os gráficos de e (orientado no sentido anti-horário). Baseado em sua resposta, diga se o campo é conservativo ou não.
Passo 1
Cara, esse campo é muito feio e a região limitada pelo nosso caminho está entre duas curvas, então ela é fechada. Por isso, vamos ver se é uma boa usar o Teorema de Green. Para testar isso, vamos calcular o rotacional desse campo
Nosso campo é
Aí o rotacional fica
Nossa, ficou super simples, né? Então, bora de Green!
Mas repara que esse rotacional não zerou. Então nosso campo não é conservativo, tá?
Passo 2
O Teorema de Green diz que a gente pode calcular a integral de em uma curva por essa relação:
Onde é uma região e é a curva fronteira dessa região. Só que ele tem umas condições para aplicar.
Primeira condição: A nossa região precisa ser fechada. Como ele já chama nosso caminho que a gente vai chamar de de fronteira da região entre curvas, a gente saca que ele é fechada.
Segunda condição: A fronteira precisa ser percorrida no sentido positivo: Que sentido é esse? Se ela for uma região sem buracos como a nossa, a gente precisa que ela esteja no sentido anti-horário.
O enunciado diz que a fronteira está nesse sentido, então tá belezinha!
Aí, podemos reescrever o lado esquerdo do teorema assim
Terceira condição: e suas derivadas não podem ter descontinuidades dentro da nossa região.
Isso também vai acontecer! Por que? O único problema que poderíamos ter é se o argumento do log zerasse, ou ficasse negativo. E isso só acontece para valores .
Maas, vamos ver mais a frente que a nossa região só está em . Então essa tá tranquilo também. Bora lá aplicar o Teorema!
Passo 3
Substituindo nele as coisas que a gente tem:
Vimos que :
Precisamos definir nossa região entre e como extremos de integração. Uma boa é esboçar essa região:
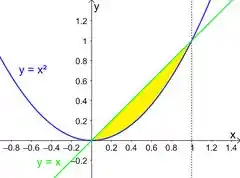
Eles esperam que a gente já saiba a carinha de e , tá? Aí temos que a interseção entre essas duas curvas ocorrem em:
Daí a gente pode dizer que no eixo , nossa região está limitada assim:
E no eixo , ela está limitada por cima por e por baixo por , assim, dizemos:
Nossa integral fica
Repara que integramos primeiro em relação a , porque ele está entre funções de .
A ideia é calcular o valor da integral de linha sobre calculando essa integral dupla da direita.
Passo 4
Bora calcular
Resposta
O campo não é conservativo.