Sejam , e pontos de e a trajetória que vai em linha reta de até e em seguida de até . Determine o trabalho ao longo de do campo de forças
Passo 1
Falaaaa... belezinha???
Nessa questão aqui vamos usar o teorema de Green:
Seja uma curva plana simples, fechada, contínua por trechos, orientada positivamente, e seja a região delimitada por . Se e têm derivadas parciais de primeira ordem contínuas sobre uma região aberta que contenha , então
Vamos desenhar essa bendita trajetória:
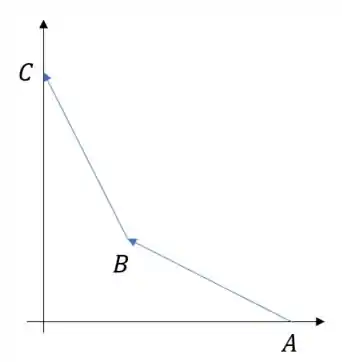
Passo 2
Cê deve estar se perguntando... Mas por que esse maluco ta falando de teorema de Green, que precisa de curva fechada, e no problema tem uma curva abertinha??
Pois muito que bem... A gente pode fechar essa curva e depois descontar lá no meio da integral. Vamos fazendo que mais pra frente vai fazer toooodo sentido, beleza?
Fechando a curva:
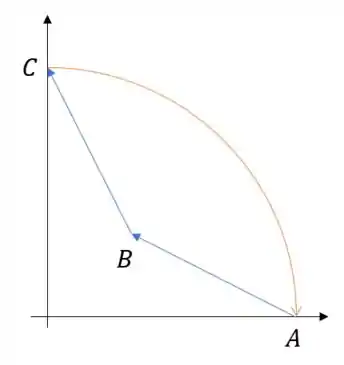
Repara que fechamos com uma parte de circunferência porque temos um bendito no denominador lá dentro da integral e isso vai ser horrível de parametrizar e resolver se a gente fechar só com uma retinha ligando do ponto A ao ponto C.
Curva fechadinha e tals, maaaas ainda temos um pequeno problema. A curva precisa estar orientada positivamente.
Uma dicona pra saber se ta orientada positivamente é a gente andar sobre a linha (doidera, né? Hahah). Se a área da parte fechada estiver à nossa esquerda ela ta orientada positivamente. Se estiver à direta, então ta orientada negativamente.
Puuuutz... no nosso problema a curva ta orientada negativamente, né? Maaas vamos mudar essa orientação:
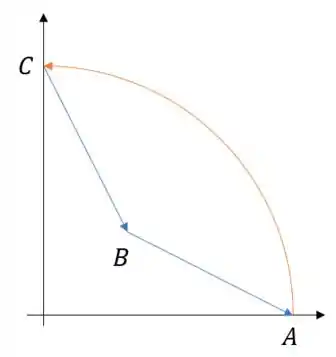
Atenção porque então vamos precisar mudar isso na integral do Teorema de Green:
Que é só a gente jogar o sinal de menos pra fora da integral:
Passo 3
Bora fazer logo esse lado direito da equação pra ver se a gente consegue se livrar logo disso:
Ufaa... deu igual a zero. Então vamos ficar com:
Passo 4
Agora falta a gente dizer quem é essa curva C. Bom... é a trajetória e a partezinha que fechamos, e vamos chamar de .
E já melhoramos mais:
Repara que o trabalho vai ser dado por:
Então temos:
Passo 5
Parametrizando : (usamos o “3” só pra ficar bonitinho... na verdade não faria muita diferença porque, SPOILER, ele vai sumir no final rsrs)
Com variando:
Daí ficamos com:
Agora é só resolver a integralzinha de linha:
Mas vamos com calma... Fazendo uma coisa de cada vez:
Fazendo o produto escalar com a derivada :
Ohhh... até que ficou bonitinho, no fim das contas, heim...
O trabalho, então, vai ser:
Ufaaa... essa foi pesadinha, né?
Mas bora pra próxima...