Seja uma função diferenciável e uma primitiva de , tal que , . Calcule
Onde está situada no primeiro octante, e é a interseção das superfícies e , percorrida no sentido anti-horário quando vista de cima.
Passo 1
Bem, para resolver essa integral de linha, não se preocupe com nada daquelas informações por enquanto ( é primitiva de e tal). Essas informações entraram conforme resolvemos a integral de linha, mas... Como resolvemos a integral de linha mesmo?
1º - Parametrizando a curva.
2º - Encontrando a derivada da parametrização.
3º - Trabalhando com a função vetorial que está sendo integrada.
Então vamos nessa!
Passo 2
Precisamos conseguir parametrizar a curva que se desenharmos é essa curvinha na intersecção aqui oh:
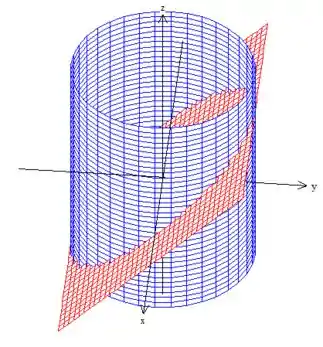
Como estamos em cima de um cilindro
vamos parametrizar essa circunferência como sempre fazemos (usando as “primas” das coordenas polares:
Como ele quer tudo isso no primeiro octante, vamos ter e isso nos diz que
Falta a componente , mas sabemos que a curva está em cima do plano...
Então
Vamos ter
Com
A orientação está de boa, porque estamos trabalhando como normalmente fazemos, no sentido anti-horário.
Passo 3
A segunda coisa é calcularmos a derivada dessa parametrização,
Passo 4
Vamos realizar a terceira tarefa que é substituir os termos da parametrização
Nos termos da função vetorial sem se preocupar com quem é agora:
Ficando
Simplificando um pouco já que ...
Passo 5
Muito bem, agora podemos retornar à integral de linha que estamos trabalhando
e substituir tudo o que encontramos...
Agora sim, como a parte da integral de linha já basicamente finalizou, vamos nos preocupar em encontrar o resolvendo essa integral aí. Vamos nessa?
Passo 6
Peguemos a mesma integral de cima, mas, para evitar escrever aqueles limites de integração toda hora, peguemos apenas a integral indefinida:
Repare que nessa integral aí, posemos realizar uma mudança de variável bem legal:
Então...
A integral vai ficar
Agora vamos entender o que ele falou da função , ele disse que ele é uma primitiva de ... Isso significa que:
Logo...
Vamos voltar para
Passo 7
Voltando a integral definida:
Vamos ter