Seja , onde é a semi-reta . Calcule
Onde é uma curva por partes, com imagem contida em , tal que e .
Passo 1
Bem, o que o exercício pede é uma integral de linha:
Nós temos o campo mas o enuciado não nos dá nenhuma curva específica, então não temos como parametrizá-la.
Então vamos torcer pra que possamos resolvê-la de outra forma... O que acha de uma função potencial? Parece uma boa ideia, vamos ver se dá!
Passo 2
A gente viu na teoria que, para podermos achar uma função potencial, o campo deve ser conservativo. Ou seja como ele está definido para toda a região (já que a reta não pertence ao conjunto dado), só precisamos verificar:
Vamos testar:
Valores meio estranhos, mas pelo menos:
Ou seja, o campo é conservativo e existe uma função potencial!
Passo 3
Se existe uma função potencial , a gente viu que:
Sendo e .
Então só falta acharmos essa nossa função potencial , vamos lembrar do método que temos:
Então:
Passo 4
Finalmente, vamos ter:
Mas, podemos ver pela circinferência trigonométrica:
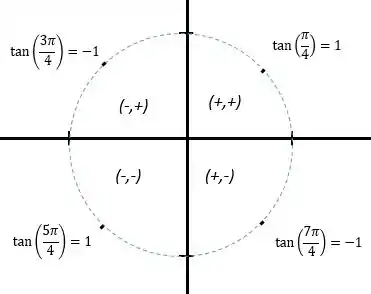
O primeiro ponto é , logo para negativo e positivo:
O primeiro ponto é , logo para positivo e positivo:
Então: