Teorema de Laplace
Teoria
O Teorema de Laplace é um método muito útil para calcula o determinante de uma matriz de ordem
O Responde Aí preparou um vídeo super completo te explicando tudo o que você precisa saber sobre Teorema de Laplace. Saca só 👇 🧡
📢 Clique para saber mais:
Como fazer o teorema de Laplace?
A gente vai aprender na prática como calcular o Teorema de Laplace! Então se liga na matriz
Para calcular o determinante de
- 1º Passo: Selecionar uma linha ou coluna, com a maior quantidade possível de elementos igual a zero;
- Para o nosso exemplo a melhor fila seria a quarta coluna, porque ela tem a maior quantidade de zeros e isso vai facilitar nossas contas
- 2º Passo: Calcular o cofator de cada elemento da fila escolhida
- 3º Passo: Somar os produtos dos números da fila selecionada pelos seus respectivos cofatores.
- No nosso exemplo vai ficar assim:
Cofator - Como Calcular?
O cofator é uma matriz de ordem
Onde:
é o cofator do elemento ; -
é o determinante da matriz resultante após a eliminação da linha e .
Eu sei que nada tá fazendo sentido, então vamos focar no exemplo que vai ficar mais claro!
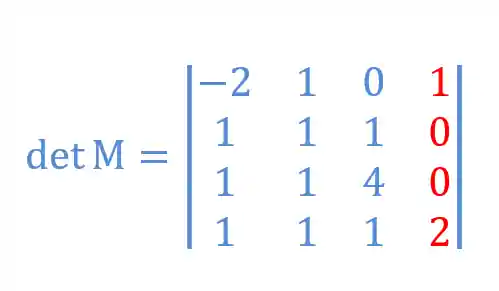
Lá em cima eu falei que precisávamos escolher uma fila com o maior número de zeros possível, lembra?!
Então, vamos precisar calcular o cofator de cada elemento dessa linha! Vamos começar com o número
Para isso a gente vai eliminar a linha e a coluna onde esse elemento esta:
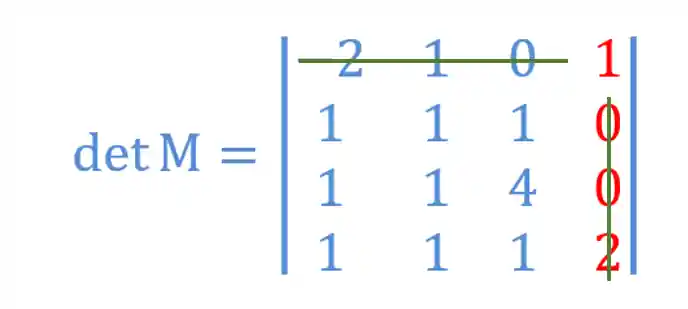
Com isso, vamos criar uma nova matriz e calcular a determinante dessa matriz:
Lembra da fórmula do cofator?
A gente vai substituir nossos valores nela:
E prontinho! Calculamos o cofator do primeiro elemento. Agora é só fazer o mesmo para os demais elementos!
No nosso exemplo, tanto o
Agora eu vou te dar o gabarito do elemento
Calcular o determinante por Laplace
Agora é só substituir os cofatores no teorema de Laplace e pronto!
Lá em cima tínhamos:
Podemos eliminar os elementos multiplicados por zero:
Substituir os cofatores:
Prontinho!!
Teorema de Laplace - Exercício Resolvido
Pra terminarmos com chave de ouro, se liga nesse exercício sobre Teorema de Laplace que eu separei pra você 👇
Bora praticar com mais exercícios?!
Teorema de Laplace - Exercício Resolvido
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Calcule o cofator do elemento da matriz abaixo:
Passo 1
Bom, o elemento é o .
Para isso, vamos montar a matriz , tirando a 4ª linha e a 3ª coluna da matriz.
Ficamos com:
Passo 2
Agora falta podemos calcular o cofator, que é dado por:
Ou seja, o cofator é o menor complementar com sinal negativo, nesse caso.
Passo 3
Agora resta calcular o determinante:
Fazendo o cálculo usando Laplace de novo:
Resposta
Exercício Resolvido #2
Elaboração Própria
Calcule o determinante da matriz .
Passo 1
O primeiro passo é perceber que essa matriz possui um número considerável de zeros, então vale a pena usar o Teorema de Laplace.
Agora, qual fila tem mais zeros?
Se você olhar direito, a fileira com mais zeros é a 2ª coluna, e é nela que vamos aplicar o Teorema.
Passo 2
Vamos calcular!
Temos que multiplicar cada elemento pelo seu cofator.
Assim:
A matriz , retirando a segunda linha e a segunda coluna, fica assim:
Passo 3
O cofator fica:
Assim:
Passo 4
Agora é só calcular esse determinante !
Posso fazer a regra de Sarrus... mas nesse caso, o jeito mais prático é usar mais uma vez o Teorema de Laplace, já que a 3 coluna desse determinante é cheia de zeros.
Não precisamos dos cofatores dos elementos que estão com zeros, apenas do elemento da linha e da coluna.
O determinante dessa matriz é o cofator vezes o elemento, .
Isso nos dá:
Resposta
.
Exercício Resolvido #3
UFRJ-P4-2015.2.1
Calcule o determinante da matriz abaixo:
Passo 1
Como a matriz é temos que usar o Teorema de Laplace.
Podemos ver que a linha/coluna que possui mais zeros é a terceira linha, logo vamos utilizá-la!
Resposta
Letra