Determinantes por Escalonamento: Como Calcular?
Teoria
Heeey! Bem vindo ao RespondeAí! Hoje você vai aprender de uma vez por todas a calcular um determinante por escalonamento!
Imagina que você tem que calcular o determinante de uma matriz bem grande, vamos supor uma matriz
E agora?! O que fazemos?!
Como calcular o determinante da matriz por escalonamento?
Sempre que a matriz for triangular (tanto superior quanto inferior), o determinante é o produto dos elementos da diagonal principal. Isso naturalmente vale para uma matriz diagonal também ;)
Ah, então nem é tão difícil esse exemplo, a nossa matriz é triangular! Então o determinante é
Seria ótimo se pudéssemos sempre escalonar uma matriz para calcular os determinantes, não? Porque é bem fácil calculá-los em matrizes que já estão escalonadas. Lembre-se que para matrizes quadradas, uma matriz escalonada vira uma matriz triangular superior!
A boa notícia é que você pode fazer isso! 🤩
Escalonamento de Matrizes
Vamos aprender fazendo um exemplo! Se liga nessa matriz 4x4:
Para escalonar essa matriz vamos fazer algumas operações simples!
Só deve tomar cuidado com três coisas:
- Quando você troca linhas ou troca colunas de lugar, o sinal do determinante muda;
- Quando você multiplica uma linha por um escalar, o determinante também é multiplicado por esse escalar;
- Se você troca uma linha/coluna por um múltiplo de uma outra somado a essa linha/coluna, o determinante não se altera.
Esquematizando, seja a matriz
OBS: Cuidado com esta última operação!! Se você fizer
Vamos usar essas propriedades para calcular o seguinte determinante:
Usamos a operação elementar para alterar a segunda linha:
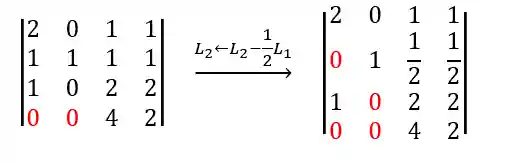
Agora a terceira:
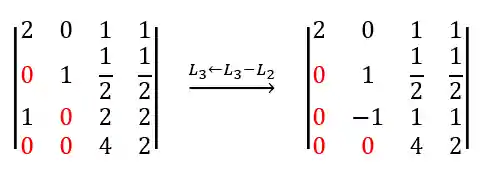
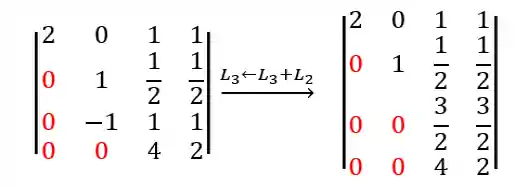
E finalmente, a última linha:
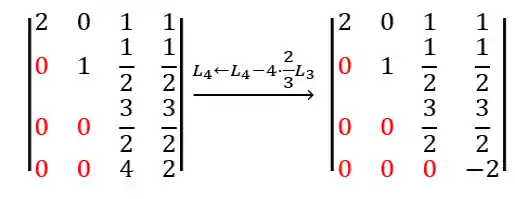
Repare que o determinante não alterou em nenhum dos casos pois usamos a operação elementar,
Bem tranquilo, né?!
Eu recomendo usar sempre a operação elementar já que esta não altera o determinante. Em alguns casos, no entanto, usar apenas ela pode criar várias frações que podem complicar muito sua vida. Então quando usar as outras operações ou não fica a seu critério, só tome cuidado com as alterações no determinante 😉
Curtiu nosso conteúdo?
Então confere esse vídeo de exercício sobre cálculo de Determinantes por Escalonamento :
Vamos exercitar mais?
Exercícios Resolvidos
Exercício Resolvido #1
Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 3ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 188 – Prob 6.2
Aplicamos em uma matriz as seguintes operações elementares:
trocamos com ;
multiplicamos por
Obtemos a matriz . Calcule .
Passo 1
Bom, primeiro vamos calcular o determinante de . Como é uma matriz triangular, temos:
Passo 2
Agora vamos ver como as operações elementares alteraram o determinante de :
trocando as linhas de lugar nós trocamos o sinal do determinante;
operação elementar, determinante inalterado;
multiplicando uma linha por , também multiplicamos o determinante por ;
Aplicando essas alterações em chegamos a :
Resposta
Exercício Resolvido #2
Elaboração Própria
Diga qual das matrizes abaixo não tem determinante nulo:
Passo 1
A matriz da letra é triangular, então seu determinante é o produto dos elementos que estão na diagonal principal:
Passo 2
Na matriz a coluna é igual à coluna multiplicada por .
Então as colunas são LD, logo seu determinante é zero. Mas você também pode calcular:
Passo 3
Na , nem as colunas nem as linhas da matriz são múltiplas uma da outra, então a matriz é , e seu determinante é diferente de zero. Mas, se quiser, podemos também calcular:
Passo 4
Aí essa já não é tão simples.
Vamos escalonar.
Fazendo e também :
Olha só, nem precisamos escalonar tudo!
Sabe por quê?
O determinante não muda quando fazemos combinações lineares entre as linhas.
E essa última matriz é , pois a linha é o dobro da ! Então a matriz original também é !
Por isso seu determinante é também!
Logo, só a matriz não tem determinante nulo.
Resposta
Apenas a matriz
Exercício Resolvido #3
Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 3ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 188 – Prob 6.8
Calcule:
Passo 1
Basta fazermos as trocas e . Chegaremos na seguinte matriz:
Como trocamos duas linhas de lugar duas vezes, multiplicamos o determinante por duas vezes. Logo, ele se permaneceu inalterado. E agora temos uma matriz triangular superior, cujo determinante sabemos calcular:
Passo 2
O procedimento é o mesmo da letra . Basta trocarmos as linhas até termos uma matriz triangular superior. Só que dessa vez não sabemos quantas linhas temos então não podemos saber qual será o sinal final do determinante.
Repare, no entanto, que isso não é um problema!! O que está sendo pedido é o módulo do determinante. Como trocar linhas apenas troca o sinal, e este não interessa pra gente, é só multiplicarmos os valores da diagonal secundária da matriz:
Resposta
Exercício Resolvido #4
Elaboração Própria
Calcule, em função de , o determinante da matriz abaixo,
Passo 1
A matriz é de ordem , então vamos escalonar. Para zerar a 1ª coluna, é só fazer
Aí fica:
Passo 2
Agora vamos tentar zerar a segunda coluna abaixo de (terceira e quarta linhas):
Então:
Passo 3
Agora é só zerar a terceira coluna na última linha, fazendo :
Passo 4
Agora a matriz é triangular, então precisamos só multiplicar os elementos da diagonal principal:
Resposta
.