Regra de Sarrus
Teoria
A Regra de Sarrus é usada quando queremos calcular determinantes de matrizes
Como se Faz a Regra de Sarrus?
A Regra de Sarrus é um método pra se calcular determinantes de matrizes de ordem
Regra de Sarrus para Matrizes 2x2
Para matrizes
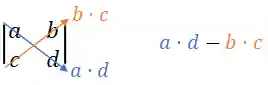
Fazemos o seguinte passo a passo:
- Passo 1: Multiplicar os elementos da diagonal primária;
- Passo 2: Multiplicar os elementos da diagonal primária;
- Passo 3: Subtrair o produto da diagonal secundária da diagonal primária.
Exemplo: Calcule o determinante:
Aplicamos a fórmula da Regra de Sarrus:
Muito rápido, né! 🤩
Regra de Sarrus para Matrizes 3x3
Para calcular determinantes de ordem
Se liga nesse esquema:
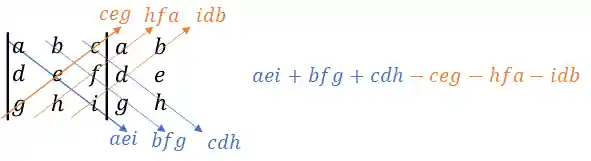
Tudo que precisamos fazer é repetir as duas primeiras colunas do lado direito, multiplicar os elementos da diagonal principal e diminuir a multiplicação dos elementos da diagonal secundária!
-Quee?! 😱
Falando assim, eu sei que parece confuso, mas confia em mim, é bem tranquilo! Bora aprender com um exemplo 👇
Exemplo: Calcule o determinante
- Passo 1: Primeiro você repete as duas primeiras colunas no lado direito:
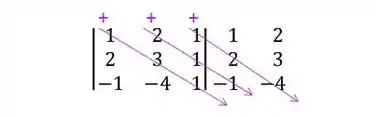
- Passo 2: Agora traçamos as linhas na diagonal principal e nas duas diagonais seguintes, indicando com um sinal de + em cima:
- Passo 3: Traçamos as linhas na diagonal secundária e nas duas diagonais seguintes, indicando com um sinal de - em cima:
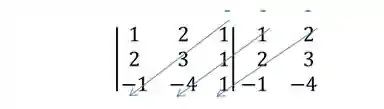
- Passo 4: Pra finalizar, somamos as diagonais principais (roxo) e subtraímos as diagonais secundárias:
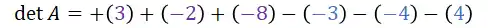
Calculando, temos:
Prontinho!
Regra de Sarrus: Vídeo Aula
Quer aprender mais sobre a regra de Sarrus? Então que tal uma vídeo aula do tema?
Aqui em baixo alguns exercícios para praticar 👇, então vamos nessa?!
Exercícios Resolvidos
Exercício Resolvido #1
Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 3ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 188 – Prob 6.1
Calcule o determinante da matriz abaixo:
Passo 1
Usando a Regra de Sarrus para ordem :
Vou botar com as setinhas pra ajudar porque é o primeiro exercício mas não vai se acostumando não em haha:
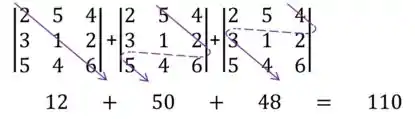
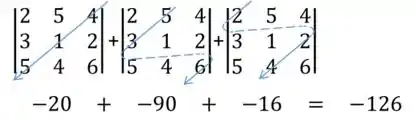
Logo,
Resposta
Exercício Resolvido #2
Elaboração Própria
Calcule o determinante:
Passo 1
Vamos usar a regra de Sarrus para ordem .
Passo 2
Agora é só lembrar que a Relação Fundamental da Trigonometria nos diz que:
Assim, o determinante pedido dá , independente do valor de .
Resposta
Exercício Resolvido #3
UFRJ-P4-2013.2
Seja , onde
O determinante da matriz é igual a:
Não é possível calcular o determinante de
Passo 1
Pô, bora calcular quem é !
Só que a linha de é o dobro da primeira, e a é o triplo!
Como suas linhas são , .
Resposta
Letra