Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Injetividade, Sobrejetividade e Bijetividade de uma TL

Ver Todos os Exercícios

Teoria

Provavelmente você já ouviu falar em funções classificadas em injetora, sobrejetora e bijetora! Com transformações lineares também temos essas definições. Bora ver como isso vai funcionar?

Transformação Linear Injetora

Lá em funções, tínhamos uma função injetora quando todos os elementos do domínio, possuíam como imagem elementos distintos do contradomínio. Essa imagem abaixo ilustra bem o que estamos falando:

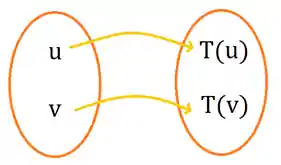
Função injetora
Função injetora

Repara como que cada elemento do domínio dá uma flechada em um elemento diferente do contradomínio? Esse é o espirito da coisa!

Quando estamos falando de uma transformação linear injetora isso significa que ela leva cada valor diferente do domínio em um valor diferente do contra domínio. Ou seja, a lógica é a mesma! Podemos escrever:

Isso quer dizer que se , então . Basicamente, uma injetiva nunca levará dois vetores diferentes no mesmo vetor! As imagens de vetores distintos são distintas!

-Show, mas na prática…como eu sei que uma TL é injetora?

Excelente pergunta! Pra saber se uma é injetora a gente vai usar o nosso querido núcleo! Se liga nesse teorema:

é

Opa, isso quer dizer que se acharmos apenas o zero como gerador do núcleo de uma , ela será injetora! Em outras palavras, quando a , será injetora. Por exemplo, pra uma transformação linear ser injetora seu núcleo deve ser apenas o vetor nulo:


Pra verificarmos se uma TL é injetora, basta ver se a dimensão do seu núcleo é 0.

-Tá, mas eu ainda não entendi direito como esse negócio vai funcionar! 😖

Então se liga nesse vídeo super completo que a gente preparou pra você! 🧡 👇

Transformação Linear Sobrejetora


Dizemos que uma TL é sobrejetiva se a imagem é completamente igual ao contradomínio.
Ou seja, todos os vetores do contradomínio também estão na imagem. A imagem está sempre contida no contra domínio da . Logo, dizer que elas são iguais implica em dizer que elas têm a mesma dimensão:

Teorema: Transformação Linear Sobrejetora
Teorema: Transformação Linear Sobrejetora

Então, para saber se uma transformação linear é sobrejetiva, basta compararmos a dimensão da sua imagem com a dimensão de seu contra domínio!

Transformação Linear Bijetora

Por fim, se uma transformação linear é injetiva e sobrejetiva ao mesmo tempo, dizemos que ela é bijetiva. Se as dimensões do domínio e do contra domínio de uma são iguais, então temos que:

éé

Temos que se é injetiva, ela também é sobrejetiva. Da mesma forma, se é sobrejetiva, ela também é injetiva. Portanto, em ambos os casos ela é bijetiva. Ter isso em mente normalmente poupa um tempo considerável na prova! No entanto lembre-se de que isso só é válido se as dimensões do domínio e do contra domínio forem iguais!

Resumo: Transformações Lineares Injetora, Sobrejetora e Bijetora

Pra fechar com chave de ouro, eu vou deixar um resuminho pra você!

  • Transformação linear Injetiva: Cada elemento do contra domínio é atingido no máximo uma vez.
  • Transformação linear Sobrejetiva: Todo elemento do contra domínio é atingido pelo menos uma vez.
  • Transformação linear Bijetiva: É uma transformação linear Injetiva e Sobrejetiva ao mesmo tempo. Todo elemento do contra domínio é atingido exatamente uma vez.

Agora vamos praticar com exercícios!

Transformação Linear Sobrejetora

Transformação Linear Bijetora

Resumo: Transformações Lineares Injetora, Sobrejetora e Bijetora

Exercícios Resolvidos

Exercício Resolvido #1

Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 3ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 126 – Fix 4.7

Seja T : V → W uma T L .

i T é sobrejetiva se, e somente se:

a dim ⁡ V = d i m ⁡ ( W )

b dim ⁡ N u c T = d i m ⁡ ( V )

c   dim ⁡ N u c T = 0

d   dim ⁡ I m T = d i m ⁡ ( W )

e   dim ⁡ I m T = 0

i i T é injetiva se, e somente se:

a dim ⁡ V = d i m ⁡ ( W )

b dim ⁡ N u c T = d i m ⁡ ( V )

c   dim ⁡ N u c T = 0

d   dim ⁡ I m T = d i m ⁡ ( W )

e   dim ⁡ I m T = 0

Passo 1

i Por definição, uma T L é sobrejetiva se:

I m T = c o n t r a   d o m í n i o

Ou, em outras palavras:

dim ⁡ I m T = d i m ⁡ ( c o n t r a   d o m í n i o )

Como na T L em questão W é o contra domínio:

dim ⁡ I m T = d i m ⁡ ( W )

Então, letra d .

Passo 2

i i Bom sabemos que uma T L é injetiva se, e somente se:

N u c T = { 0 }

Em outras palavras:

dim ⁡ N u c T = 0

Logo, letra c

Resposta

i Letra d .

i i Letra c .

Exercício Resolvido #2

Elaboração Própria

Dada a transformação abaixo:

T x , y = x + y , x - y , 2 x

a Ache uma base para a imagem de T e a sua dimensão;

b Verifique se T é bijetiva.

Passo 1

a Para calcular geradores para a imagem de T , basta “abrir” a transformação:

x + y , x - y , 2 x = x 1,1 , 2 + y ( 1 , - 1,0 )

Assim, como os geradores são L I , uma possível base para a imagem de T é:

α = 1,1 , 2 , 1 , - 1,0

Logo:

dim ⁡ I m T = 2

Passo 2

b Para saber se T é bijetiva, ela deve ser injetiva e sobrejetiva ao mesmo tempo. Olhando para a fórmula da nossa transformação podemos ver:

T : R 2 → R 3

Como o contra-dominio é o R 3 , sua dimensão é 3. A gente sabe também que dim ⁡ I m T = 2 e, portanto, a dimensão da imagem é diferente da dimensão do contra-domínio.

Logo, a transformação não é sobrejetiva. Como não é sobrejetiva, ela não pode ser bijetiva.

Resposta

a ) α = { 1,1 , 2 , 1 , - 1,0 } e dim ⁡ I m T = 2 .

b ) Não.

Exercício Resolvido #3

Transformações Lineares e Teorema Núcleo-Imagem

Seja T : R n ⟶ R m transformação linear injetivas.

Prove que se v 1 , v 2 , … , v s ∈ R n são vetores linearmente independentes, então os vetores T v 1 , T v 2 , … , T v s ∈ R m são também linearmente independentes.

Passo 1

Primeiro passo a se fazer é separar em hipótese e tese:

Hipótese: v 1 , v 2 , … , v s ∈ R n são vetores linearmente independentes

Tese: T v 1 , T v 2 , … , T v s ∈ R m são também linearmente independentes.

Nosso objetivo é provar que T v 1 , T v 2 , … , T v s ∈ R m são linearmente independentes (ou seja, nenhum deles é combinação linear do outro) usando que v 1 , v 2 , … , v s ∈ R n são vetores L I .

Queremos provar que a tese é verdadeira ( T v 1 , T v 2 , … , T v s ∈ R m são linearmente independentes), para isso precisamos que:

a 1 T v 1 + a 2 T v 2 + … + a s T v s = 0

Para esses vetores não serem uma combinação linear a única solução para essa equação seria a trivial logo, queremos achar que a 1 = a 2 = … = a s = 0 , para provar que T v 1 , T v 2 , … , T v s são L I .

Passo 2

Continuando, vamos passar os coeficientes “para dentro” da transformação, já que ela é linear:

T a 1 v 1 + T a 2 v 2 + … + T a s v s = 0

E agora vamos juntar as somas, também porque nossa transformação é linear:

T a 1 v 1 + a 2 v 2 + … + a s v s = 0

No enunciado sabemos que a nossa T é injetiva, então:

T a 1 v 1 + a 2 v 2 + … + a s v s = 0     ⇔     a 1 v 1 + a 2 v 2 + … + a s v s = 0

Mas por hipótese sabemos que { v 1 , v 2 , … , v s } é L I . Logo, se

a 1 v 1 + a 2 v 2 + … + a s v s = 0

A única solução possível seria a trivial, ou seja:

a 1 = a 2 = … = a s = 0

E assim provamos que { T v 1 , T v 2 , … , T v s } é L I .

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #4

Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 3ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 126 – Prob 4.11

Seja W = p ∈ P 3 p 0 = 0 e D : W → P 3 definida por D p = p ' . Mostre que D é injetiva.

Passo 1

Para que D seja injetiva, ela tem que satisfazer a igualdade abaixo:

N u c D = 0

Vamos começar descobrindo o que D faz. Bom, ela leva vetores de W em suas derivadas.

Passo 2

O conjunto W é um conjunto de vetores da forma p = a x 3 + b x 2 + c x + d que satisfaçam a condição p 0 = 0 . Ou seja,

a 0 + b 0 + c 0 + d = 0

d = 0

Logo, W é formado por polinômios do tipo a x 3 + b x 2 + c x + 0 . E o vetor nulo de W é 0 x 3 + 0 x 2 + 0 x + 0 .

Passo 3

Então, temos:

D a x 3 + b x 2 + c x + 0 = 3 a x 2 + 2 b x + c

Para encontrarmos o núcleo de D basta igualarmos ela ao vetor nulo do domínio W :

3 a x 2 + 2 b x + c = 0 x 3 + 0 x 2 + 0 x + 0

Se achar mais fácil de entender, pode escrever p em função da base x 3 , x 2 , x , 0 :

D a , b , c , 0 = 0,3 a , 2 b , c

0,3 a , 2 b , c = 0,0 , 0,0

Daí,

0 = 0 3 a = 0 2 b = 0 c = 0

A única solução para o sistema é:

a = b = c = 0

Logo,

N u c D = { 0 }

Portanto, D é injetiva.

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

Seja a um vetor em R 3 fixado. Decida se a fórmula T v = a × v define um operador linear injetor de R 3 . Explique seu raciocínio.
Seja E uma matriz elementar 2 × 2 fixada. Decida se a fórmula T A = E A define um operador linear injetor de M 2 × 2 . Explique seu raciocínio.
Em cada parte, determine se a multiplicação por A é uma transformação linear injetora. A = 1 - 2 2 - 4 - 3 6 A = 1 3 5 7 2 - 1 2 4 - 1 3 0 0 A = 4 - 2 1 5 5 3
Seja a aplicação T :R 2 → R 3 x , y → ( x + k y ,x + k ,y ) Verificar em que caso(s) T é linear:a) k = x b) k = 1 c) k = 0
Consideremos a transformação linear T : R 2 → R 2 definida por T x , y = ( 3 x - 2 y ,x + 4 y ) . Utilizar os vetores u = ( 1 ,2 ) e v = ( 3 , - 1 ) para mostra que T 3 u + 4 v = 3 T u + 4 T ( v ) .