Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 18.Exercício - Ex. 25b
Sejam e . Nos casos do exercício anterior, obtenha equações do lugar geométrico dos pontos médios dos segmentos paralelos a com uma extremidade em e outra em . Descreva o lugar gométrico.
(b) e
Passo 1
(b) Vamos começar olhando para as equações desses planos. O plano é:
E o plano é:
Logo de cara você pode perceber que as duas equações são bem parecidas! Elas só diferem por aquela constante ali na segunda equação.
Quando a gente tem uma equação do plano com essa forma geral aqui:
O vetor formado por esses coeficientes:
É normal ao plano!
Vamos essa regra para encontrar os vetores normais a cada um dos planos:
Os dois vetores são proporcionais um ao outro (nesse caso inclusive são iguais). Isso quer dizer que os planos são paralelos.
Como as equações e não são proporcionais uma a outra (por conta daquela constante ali na segunda), então eles são paralelos e distintos.
Passo 2
Então tá, a gente tem dois planos paralelos, vamos fazer um desenho aproximado da situação:
Se temos dois planos paralelos é fácil descobrir qual o lugar geométrico formado pelos pontos médios entre eles.
No meio do caminho entre dois planos paralelos, temos simplesmente outro plano paralelo.
Como fica a equação desse plano? Bom, a distância entre os nossos dois planos é constante e igual a . Essa distância é dada pela constante na segunda equação:
Então a equação no plano no meio do caminho entre esses dois é:
Pronto! Essa é a equação que estávamos procurando.
Passo 3
Vamos tentar resolver esse problema por argumentos geométricos.
No caso de cima, a gente viu que, entre qualquer par de pontos e , você pode traçar um segmento, e o ponto médio desse segmento está sempre contido naquele plano vermelho do desenho:
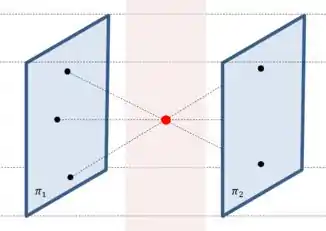
Mas percebeu uma coisa? Cada ponto no plano vermelho pode ser “gerado” por infinitos segmentos pontilhados entre em e !
O que vai mudar se a gente só usar os segmentos que sejam paralelos a um segmento ?
Todos os pontos vermelhos vão continuar aonde estão! Porque sempre vai haver pelo menos um segmento que seja paralelo a para “gerá-lo”.
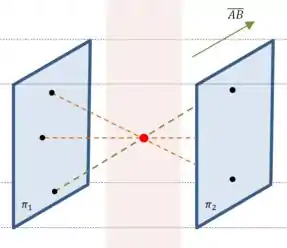
Passo 4
Ou seja, quando você acrescenta a condição de que os segmentos tem que ser paralelos a um vetor , nada muda!
E o lugar geométrico ainda é um plano paralelo a e :
Resposta
O lugar geométrico é um plano paralelo a e a , com equação .