Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 24.Exercício - Ex. 26

Sendo u → e S como no Exercício Resolvido 24 - 13 , obtenha uma equação do conjunto Ω , reunião das retas paralelas a u → que determinam, com S , cordas de comprimento 3

Passo 1

O dito S do exercício 13 (o resolvido) é igual a:

x 2 + y 2 + z 2 = 1

E u → será:

u → = ( 2 , - 1,1 )

E por Pitágoras conseguimos ver que há algum círculo na esfera que:

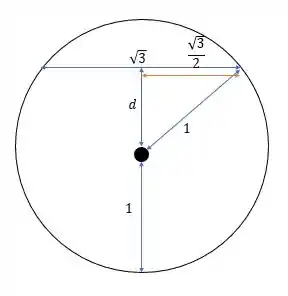
Ou:

d 2 + 3 2 2 = 1 → d = 1 2

Então a corda está distante do centro há uma distância de 1 / 2 .

Passo 2

Então queremos saber a região Ω que dista 1 / 2 do seu centro e que seja paralela ao vetor u → .

Imagine um ponto X = ( x , y , z ) que pertence a esse conjunto Ω junto com a reta paralela u → dada e considere T = m , n , p pertencente a uma esfera de raio 1 / 2 , concêntrica com a esfera S .

m , n , p = x , y , z + λ ( 2 , - 1,1 )

Aplicando esse ponto na esfera de raio 1 / 2 nós teremos:

( x + 2 λ ) 2 + ( y - λ ) 2 + ( z + λ ) 2 = 1 4

Pois devemos colocar na equação da esfera a parcela ρ 2 = 1 2 2

( x + 2 λ ) 2 + ( y - λ ) 2 + ( z + λ ) 2 - 1 4 = 0

Abrindo essa equação nós teremos:

6 λ 2 + 4 x - 2 y + 2 z λ + x 2 + y 2 + z 2 - 1 4 = 0

E fazendo o Δ dessa equação do segundo grau ser zero nós teremos:

Δ = 4 x - 2 y + 2 z 2 - 24 x 2 + y 2 + z 2 - 1 4 = 0

Simplificando esse Δ nós teremos:

Δ = 2 2 x - y + z 2 - 12 x 2 + y 2 + z 2 - 1 4 = 0

O gráfico da esfera com a região Ω deixa mais claro o que queremos.

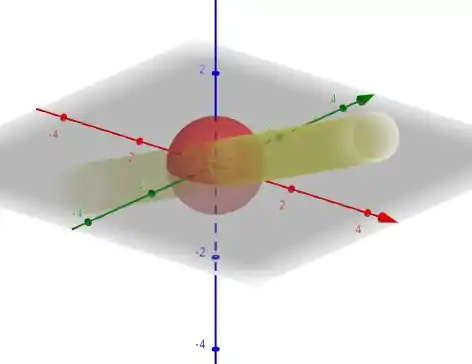
Uma região cilíndrica concêntrica com a esfera, e que dista 1 / 2 do seu centro.

Resposta

2 2 x - y + z 2 - 12 x 2 + y 2 + z 2 - 1 4 = 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Obtenha equações da circunferência circunscrita ao triângulo PQR, nos casos: P = 3 , - 1 , - 2 , Q = 1,1 , - 2 e R = - 1,3 , 0 . P , Q e R são os pontos de interseção do plano π : 3 x + 2 y + 6 z = 6
Nas condições da proposição anterior:Exprima d C 1 , π em função de ρ 1 , ρ 2 , δ ;Mostre que d C 1 , π ≤ d ( C 2 , π ) (dos dois centros, o mais próximo de π é o da superfície esférica menor);Seja N
Obtenha equações da circunferência circunscrita ao triângulo PQR, nos casos: P = 3 , - 1 , - 2 , Q = 1,1 , - 2 e R = - 1,3 , 0 . P , Q e R são os pontos de interseção do plano π : 3 x + 2 y + 6 z = 6
Obtenha uma equação da superfície esférica inscrita no tetraedro determinado pelos planos π 1 : y = 3 π 2 : z + 2 = 0 π 3 : 2 x - 2 y - z + 4 = 0 π 4 : 2 x + y - 2 z = 13
Dados o ponto P e a superfície esférica S de centro C e raio ρ , sejam α = d P , C e r uma reta que contém P e intercepta S nos pontos A e B (eventualmente, iguais). Seja D o simétrico de B em relação