Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Norma de um Vetor

Ver Todos os Exercícios

Teoria

Fala aí! Você esta no Responde Aí! Bora lá aprender sobre a norma de um vetor?!

O que é a norma de um vetor?

De maneira simples, a norma de um vetor que também é chamado de módulo de um vetor é um número real que representa o comprimento desse vetor.

Dá uma olhada aqui:

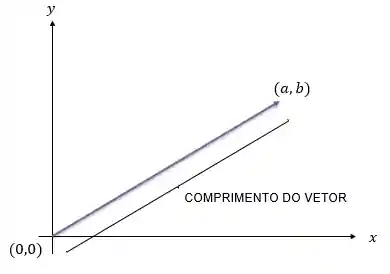
Exemplo de um vetor com coordenadas a e b
Exemplo de um vetor com coordenadas a e b

Note que o comprimento do vetor é a distância entre a origem, ponto , e o ponto . Então para sabermos a norma do vetor temos que calcular esse comprimento.

Beleza, faz sentido, não é?

Como calcular norma de um vetor?

Para a nossa sorte tem uma fórmula bem tranquila para calcular a norma de um vetor.

Para um vetor com duas componentes: , a norma, representada por , será dada por:

E podemos também expandir essa fórmula para um vetor com três, quatro, ou componentes. Seja , a norma será:

Bem de boas!

Graças...
Graças...

Vetor unitário

Um vetor é unitário é um vetor com módulo igual a .

Para representar vetores unitário nós usamos o acento circunflexo ao invés de da seta .

Um vetor unitário pode ser usado quando queremos representar apenas uma direção sem se preocupar com o módulo.

Por isso, podemos pegar um vetor qualquer e descobrir o vetor unitário que aponta para a mesma direção. Fazemos isso dividindo o vetor pela sua norma.

Dizemos que é a normalização de .

Exemplo

Diga se os vetores e são vetores unitários e se não forem normalize-os.

Para sabermos se são ou não unitários temos que encontrar a norma.

Podemos dizer que é um vetor unitário, mas não é. Então agora vamos normalizar o vetor .

Observe que quando você normaliza um vetor você apenas multiplica ele por um número real positivo. Ou seja, o vetor normalizado e o vetor original possuem a mesma direção e sentido! É como se tivéssemos comprimido o vetor azul:

Representação gráfica da normalização de um vetor
Representação gráfica da normalização de um vetor

Relação entre produto interno e a norma de um vetor.

Além de tudo isso, ainda podemos relacionar a norma de um vetor com o produto interno dele com ele mesmo 😱.

Imagina novamente o vetor , o produto interno dele com ele mesmo é dado por:

$$=u_1.u_1+u_2.u_2+u_3.u_3+...+u_n.u_n=u_1^2+u_2^2+u_3^2+...+u_n^2$$

Note que essa expressão do produto interno do vetor com ele mesmo é exatamente o que tem dentro da raiz quadrada na fórmula de definição de norma:

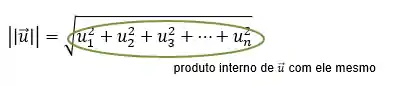
Relação entre produto interno e norma de um vetor
Relação entre produto interno e norma de um vetor

Então, podemos reescrever a norma como:

$$||\vec{u}||=\sqrt{}$$

Podemos ainda reorganizar e escrever o produto interno em função da norma:

$$={||\vec{u}||}^2$$

Ou seja, podemos dizer que o produto interno de um vetor por ele mesmo é igual ao módulo do vetor ao quadrado.

Assim, podemos a partir da norma achar o produto interno e vice e versa, tudo depende do que a questão nos fornece!

Propriedades da norma de um vetor

Para finalizar vou te mostrar algumas propriedades da norma de um vetor:

  • (vetor nulo tem norma zero);
  • se, e somente se, (o único vetor com norma zero é o vetor zero);
  • para todo (vetor multiplicado por escalar tem norma modificada por módulo do escalar)

Pronto! Agora finalizamos o conteúdo.

Eba!
Eba!

Mas que tal você dar uma olhada nessa vídeo aula sobre o assunto:

Vamos lá praticar com os exercícios! 😉

Como calcular norma de um vetor?

Vetor unitário

Relação entre produto interno e a norma de um vetor.

Propriedades da norma de um vetor

Exercícios Resolvidos

Exercício Resolvido #1

UFRJ-2013.2-14

Considere o produto interno usual de R 4 e sejam u → = ( 2,0 ,   1 , - 1 ) e   v → = ( 2 ,   1 ,   1 ,   1 ) .

Calcule a distância de u → a v → .

a   5

b   5

c   1

d - 1

Passo 1

A distância é dada pela norma de u → - v → .

Fica assim:

u → - v → = 2 - 2,0 - 1 ,   1 - 1 ,   - 1 - 1

u → - v → = ( 0 ,   - 1 ,   0 ,   - 2 )

u → - v → = 0 2 + - 1 2 + 0 + - 2 2

u → - v → = 5

Resposta

Letra a

Exercício Resolvido #2

Alfredo Steinbruch e Paulo Winterle, Álgebra Linear, 2ª ed., São Paulo, Pearson, 1987, pp. 143. – 6

Se

u = a 1 b 1 c 1 d 1   e   v = a 2 b 2 c 2 d 2

são matrizes quaisquer de M 2 × 2 , a seguinte fórmula define um produto interno nesse espaço:

u ∙ v = a 1 a 2 + b 1 b 2 + c 1 c 2 + d 1 d 2

Dados os vetores

u = 1 2 - 1 1   e   v = 0 2 1 1

determinar u + v

Passo 1

-

Temos que:

u + v = 1 2 - 1 1 + 0 2 1 1 = 1 4 0 2

Agora precisamos calcular u + v :

u + v = u + v , u + v = 1 2 + 4 2 + 0 2 + 2 2 = 21

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #3

Alfredo Steinbruch e Paulo Winterle, Álgebra Linear, 2ª ed., São Paulo, Pearson, 1987, pp. 143. – 5

Consideremos o seguinte produto interno em P 2 : p ∙ q = a 2 b 2 + a 1 b 1 + a 0 b 0 , sendo p = a 2 x 2 + a 1 x + a 0 e q = b 2 x 2 + b 1 x + b 0 . Dados os vetores p 1 = x 2 - 2 x + 3 , p 2 = 3 x - 4 e p 3 = 1 - x 2 , calcular:

a   p 1 ∙ p 2

b   ‖ p 1 ‖ e p 3

c   p 1 + p 2

d p 2 p 2

Passo 1

a Pelo produto interno definido, temos que:

p 1 ∙ p 2 = 1 ∙ 0 + - 2 ∙ 3 + 3 ∙ - 4 = - 6 - 12 = - 18

Passo 2

b Sabemos que p = p , p . Então:

p 1 = 1 2 + - 2 2 + 3 2 = 14

p 3 = ( - 1 ) 2 + 0 2 + 1 2 = 2

Passo 3

c Primeiro achamos p 1 + p 2 :

p 1 + p 2 = x 2 - 2 x + 3 + 3 x - 4 = x 2 + x - 1

Agora a norma:

p 1 + p 2 = x 2 + x - 1 = x 2 + x - 1 , x 2 + x - 1 = 1 2 + 1 2 + - 1 2 = 3

Passo 4

d Temos que p 2 = 3 x - 4 e que a norma dele é:

p 2 = 0 2 + 3 2 + - 4 2 = 25 = 5

Portanto:

p 2 p 2 = 3 x - 4 5

Resposta

a - 18

b   14 e 2

c   3

d   3 x - 4 5

Exercício Resolvido #4

UFRJ – 2015.2 - Lista 5

Seja u = A v . Classifique em Verdadeira ou Falsa as afirmações abaixo:

A Cada componente de u é o produto interno de v com uma linha de A

B   Se tanto v quanto as linhas de A são vetores unitários, então todas as componentes de u tem módulo menor que 1

C   Se v é não-nulo e pertence à imagem de A , então u nunca será o vetor nulo

D   Se v pertence ao núcleo de A , então u sempre será o vetor nulo

Passo 1

Vamos verificar letra por letra então ;)

A   Cada componente de u é o produto interno de v com uma linha de A

Bom, o que fazemos quando multiplicamos uma matriz por um vetor? Vamos tomar A uma matriz 2 × 2 e v um vetor do R 2 :

u 1 u 2 = a b c d v 1 v 2

u 1 u 2 = v 1 a + v 2 b v 1 c + v 2 d

Logo:

u 1 = a , b , v 1 , v 2

u 2 = c , d , v 1 , v 2

Fiz com vetores do R 2 e uma matriz 2 × 2 quadrada pra facilitar o entendimento, mas não é difícil perceber que isso vale para qualquer produto matriz vetor. Logo, essa afirmativa é verdadeira.

Passo 2

B   Se tanto v quanto as linhas de A são vetores unitários, então todas as componentes de u tem módulo menor que 1

Óbviamente não. Vamos pegar um exemplo qualquer:

1 0 = 1 0 0 1 1 0

Todas as linhas de A são vetores unitários, assim como o vetor v . No entanto, o módulo da primeira componente de u = 1,0 vale 1 . Logo, não possui módulo menor que 1 .

Logo, falsa.

Passo 3

C   Se v é não-nulo e pertence à imagem de A , então u nunca será o vetor nulo

Essa é chatinha. Vou te dar um contra-exemplo pra provar que é falsa.

0 0 0 = 1 1 - 1 1 1 - 3 1 1 - 2 1 - 1 0

Bom, v = 1 , - 1,0 claramente não é o vetor nulo. Além disso, temos que:

1 1 - 1 1 1 - 3 1 1 - 2 1 1 1 = 1 - 1 0

Logo, 1 , - 1,0 pertence à imagem de A . No entanto, vemos que u é o vetor nulo. Portanto, a afirmativa é falsa.

Passo 4

D   Se v pertence ao núcleo de A , então u sempre será o vetor nulo

Verdadeira. Se tiver marcado falsa vou até sua casa te bater rapá. Por definição, se v pertence ao núcleo de A , temos A v = 0 . Logo, u sempre será o vetor nulo.

Resposta

A   V

B   F

C   F

D   V

Exercício Resolvido #5

Elaboração própria

Em um espaço com o produto interno usual, assinale o vetor que possui a menor norma:

a) ( 4 ,   7 ,   0 ,   2 )

b) ( 5 ,   8 ,   13 ,   1 )

c) ( 8 ,   5 ,   9 ,   0 )

d) ( 0 ,   5 ,   4 ,   7 )

Passo 1

O produto interno usual é aquele escalar mais normalzão beleza? A gente vai calcular a norma de cada alternativa a partir desse produto interno pra aí sabermos qual dos vetores tem a menor norma :)

Vamos lá!

Passo 2

a) A norma desse vetor é dada por:

4 2 + 7 2 + 0 2 + 2 ²

16 + 49 + 4

69

b) Fazendo o mesmo processo:

5 2 + 8 2 + 13 2 + 1 2

25 + 64 + 169 + 1

259

c) O penúltimo, vamo que vamo:

8 2 + 5 2 + 9 2 + 0 ²

64 + 25 + 81

170

d) E por fim:

0 2 + 5 2 + 4 2 + 7 2

25 + 16 + 49

90

Agora é só vermos qual tem a menor norma :) no caso é a letra A, certo? É isso aí! :D

Resposta

a) ( 4 ,   7 ,   0 ,   2 ) (norma 69 )

Exercício Resolvido #6

Elaboração própria

Dados os vetores u → , v → e w → , sabe-se que u → = 6 , v → = 9 , w → é unitário, u → . v → = 4 , u → . w → = v → . w → = 8 . Qual o comprimento do vetor u → + v → + w → ?

Passo 1

Sabemos que

u → + v → + w → 2 = u → + v → + w → . u → + v → + w →

Fazendo a distributiva:

u → + v → + w → 2 = u → 2 + u → . v → + u → . w → + v → . u → + v → 2 + v → . w → + w → . u → + w → . v → + w → ²

Substituindo os valores dados pelo enunciado:

u → + v → + w → 2 = 36 + 4 + 8 + 4 + 81 + 8 + 8 + 8 + 1

u → + v → + w → 2 = 158

Então, colocando raíz quadrada dos dois lados, temos

u → + v → + w → = 158

Resposta

u → + v → + w → = 158

Exercício Resolvido #7

Elaboração própria

Dada a matriz

A = 2 4 6 3

Seja o produto interno ⋅ , ⋅ A definido por

u → ,   v → A = u → T . A . v →

Calcule a norma do vetor u → = 4 7 .

Passo 1

Vimos que para calcular a norma de um vetor, vamos fazer a raíz, quadrada do produto interno dele com ele mesmo certo? Logo:

u → = u → ,   u → A

Aí é só aplicarmos o produto interno dado pelo enunciado :D

Passo 2

Aplicando o produto interno:

u → = u → T . A . u →

u → = [ 4 7 ] . 2 4 6 3 . 4 7

Multiplicando as matrizes:

u → = [ 50 37 ] . 4 7

u → = [ 459 ]

Logo, a norma do vetor é:

u → = 459

Resposta

u → = 459

Exercício Resolvido #8

UFRJ, Álgebra Linear, P3 – 2015/1 - Adaptado

Considere os vetores u → = 5 , 0 , 7 e v → = 4 , 0 , 6 . Assinale abaixo o vetor que está na direção de v → e possui o mesmo tamanho de u → :

a) 4 52 0 6 52

b) 4 74 52 0 6 74 52

c) 4 74 0 6 74

d) 22 52 0 33 52

Passo 1

Calculando o tamanho de u → :

u → = 5 , 0 , 7 , 5 , 0 , 7 = 25 + 49 = 74

Agora bora calcular a norma de v → :

v → = 4 , 0 , 6 , 4 , 0 , 6 = 16 + 36 = 52

Passo 2

Sabemos que se multiplicarmos/dividirmos um vetor por qualquer escalar, ele vai manter a sua direção. Então a nossa resposta vai ser o vetor v → multiplicado ou dividido por algum escalar certo?

Se dividirmos o vetor v → por 52 , vamos ter um vetor unitário na direção v → .

Opa, mas não queremos um vetor unitário, queremos que ele tenha o tamanho de u → !!

Legal, então é só multiplicar o vetor unitário que temos pela norma de u → , ou seja, 74 .

v → ∙ 74 52 = 4 74 52 0 6 74 52

Então a alternativa correta é a letra B de bola :D

Resposta

b) 4 74 52 0 6 74 52

Exercícios de Livros Relacionados

Seja T um isomorfismo de um espaço vetorial V. Provar que se u , v é um produto interno sobre V, então o mesmo acontece com a função P T : V × V → R definida por P T ( u , v ) = T ( u ) , T ( v ) .
Sejam f ( t )=a 0 + a 1 t + a 2 t ² + . . . + a n t n e ² g ( t )=b 0 + b 1 t + b 2 t ² + . . . + b n t n ² polinômios quaisquer de P n ( R ) . A função ( f ( t ) , g ( t ) ) →a 0b 0 + a 1 b 1 + . . .
Seja V = R 4 munido do produto interno usual, determinar um vetor não nulo v ∈ R 4 que seja ortogonal a v 1 = ( 1 ,1 ,1 ,- 1 ) , v 2 = ( 1 ,2 ,0 ,1 ) e v 3 = ( - 4 ,1 ,5 ,2 ) .
No espaço V = P 2 consideremos o produto interno f t ∙ g t =∫ 0 1 f t ∙ g td t . Calcular f t ∙ g t e | f t | para f t = t 2 - 2 t e g t = t + 3 .
Consideremos no R 3 , o seguinte produto interno: x 1 , y 1 , z 1 ∙ x 2 , y 2 , z 2 = 2 x 1 x 2 + y 1 y 2 + 4 z 1 z 2 Determinar, em relação a esse produto interno, um vetor unitário simultaneamente o