Distância entre Planos
Produzido por Aline BuzziTeoria
Bora aprender como calcular a distância entre planos?!
Se você já sabe calcular a Distância entre Ponto e Plano você vai perceber que é bem parecido.
A principal diferença é que aqui você tem que ficar ligado na Posição Relativa entre Planos, para saber se os planos são transversais ou perpendiculares.
Agora vamos para o que interessa!
Calcular a Distância entre dois Planos
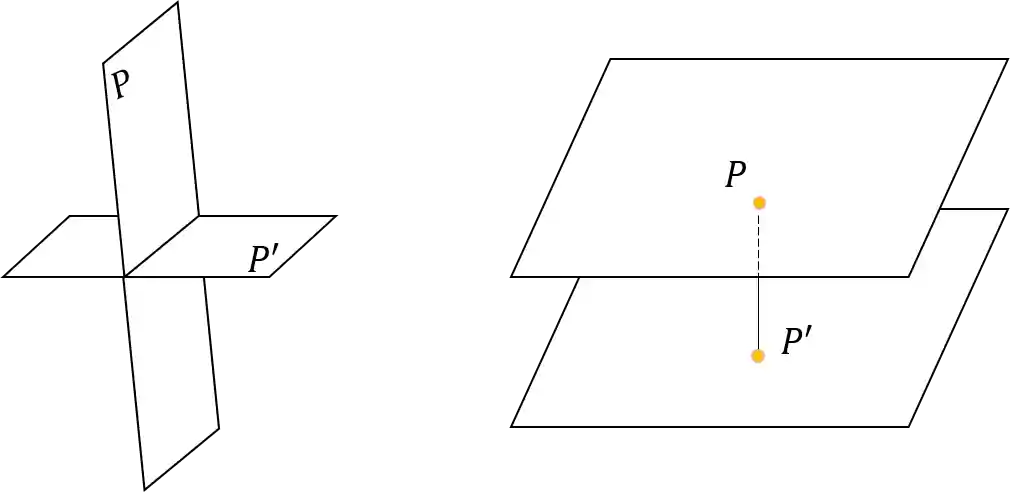
Se os planos forem transversais, então a distância entre eles é ZERO.
Já se eles forem paralelos, faremos da seguinte forma:
- Escolheremos um ponto pertencente à um dos planos
- Escolhido o ponto, calcularemos a distância entre esse ponto escolhido até o outro plano por meio da fórmula de distância entre plano e ponto.
Mas agora, como saber se os planos são transversais ou paralelos?
É o que a gente vai descobrir agora!
Posição Relativa entre Planos
Para saber a relação entre dois planos quaisquer, a gente tem que prestar atenção na equação dos planos.
A seguir tem uma tabelinha resumo para você saber a posição relativa entre os planos:

Bem tranquilo, não é?
Exemplo:
Agora pra acabar, vamos ver um exemplo!
Qual é a distância entre o plano
Podemos perceber que
Vamos escolher um ponto qualquer de algum dos planos.
Eu escolhi o ponto
Agora é substituir essas coordenadas na fórmula de distância entre ponto e plano:
Logo:
E essa é exatamente a distância entre os dois planos!!!! UHULLLL
Nossa teoria fica por aqui! Mas você pode conferir esse mesmo conteúdo em vídeo, clicando aqui em baixo!
Agora podemos exercitar!
Exercícios Resolvidos
Exercício Resolvido #1
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 203-11a.
Calcular a distância entre os planos paralelos:
e
Passo 1
Belezinha, vamos começar!
Para gente descobrir essa distância precisamos de um ponto de um dos planos e dos coeficientes do outro plano.
Vou escolher o ponto de . Assim, nos resta e
Agora é só jogar tudo na fórmula de distância de ponto a plano!
Resposta
Exercício Resolvido #2
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 203-11b.
Calcular a distância entre os planos paralelos:
e
Passo 1
Esse exercício é idêntico ao anterior, olha só:
Vamos escolher o ponto de . Assim, nos resta e
Agora é só jogar tudo na fórmula de distância de ponto a plano e partir para o abraço!
Resposta
Exercício Resolvido #3
Lista 2- Unicamp –Ex 13
- Encontre a distância do plano e o ponto
- Encontre a distância perpendicular entre os planos (paralelos): e
- Verifique que a reta e é paralela ao plano e encontre a distância perpendicular entre eles.
Passo 1
Esse exercício mescla o cálculo de várias distâncias. O item nós já fizemos na questão anterior, mas nunca é demais treinar ainda mais quando essa é uma questão que envolve a decoreba de uma fórmula!! ;). O item é a distância entre dois planos. E para terminar, o item a distância entre reta e plano.
Passo 2
- Devemos encontrar a distância entre o plano e o ponto . Sabemos que para calcular essa distância temos a fórmula:
- Nesse item temos a equação geral de dois planos e queremos calcular a distância entre eles. Porque o enunciado falou em distância perpendicular? É só para enfatizar que a distância que devemos calcular é a menor distância entre os planos!
- Para finalizar, último item!! Nesse item devemos primeiro verificar que a reta e o plano que nos são dados são paralelos.
No nosso caso e . Colocando os valores na fórmula e calculando, temos:
Chegamos na distância em que queríamos:
Passo 3
O enunciado nos dá uma informação preciosa: de que os planos são paralelos, ou seja, possuem uma distância entre si!! Então, se eles são paralelos e para calcular a distância entre eles vamos escolher um ponto de um dos planos e calcular a distância de ponto a plano ;).
Temos as seguintes equações gerais:
Vamos pegar um ponto da equação . Sabemos que e são coordenadas de um ponto pertencente ao plano. Assim, se chutarmos que e , quanto vale Vamos jogar na expressão os valores de e para descobrir:
Portanto, temos o ponto . Lembrando, que poderíamos escolher qualquer outro ponto desde que satisfizesse a equação do plano.
Agora, só falta calcular pela fórmula a distancia do ponto ao outro plano. Colocando os valores na fórmula, temos:
Já estamos craques em calcular a distância entre ponto e plano ;)
Passo 4
Bom, para verificarmos o paralelismo como vimos no tópico “Posições Relativas de Retas e Planos” se temos o vetor diretor da reta e a equação geral do plano com vetor normal , basta verificarmos se:
E então testar um ponto para verificar se são paralelos ou se a reta está contida no plano.
Vamos retirar da expressões que temos as informações:
Assim,
Já verificamos que só falta verificar que um ponto qualquer da reta não pertence ao plano. Pegando o ponto que pertence á reta e substituindo na equação geral do plano:
Portanto, a reta está contida no plano, ou seja, a distância entre eles é ZERO.
Resposta
Exercício Resolvido #4
Lista 2 – Unicamp – Ex 17
Considere as reta e dadas por: e ; e ;
- Mostre que e são reversas
- Encontre os planos e tais que: e é paralelo a
- Encontre a distância entre os planos e do item anterior
- Encontre em e em tais que a reta que passa por e seja perpendicular a e a .
Passo 1
- Temos que mostrar que as retas e são reversas. Para isso devemos fazer o produto misto entre os vetores e o mesmo deve dar diferente de ZERO.
- Agora, devemos determinar quais são os planos e de forma que: e é paralelo a . Temos a seguinte figura:
- Vamos agora calcular a distância entre os plano e . Como é a distância entre planos, vamos escolher um ponto de um dos planos e fazer a distância do ponto escolhido até o outro plano. Se escolhermos o ponto , então o plano para calcularmos a distância será , teremos . Colocando na fórmula, temos:
- Ufa!! Está quase terminando!! Uhulll
Vamos primeiro retirar as informações:
Com esses dados vamos montar o produto misto :
Portanto, as retas são reversas.
Passo 2
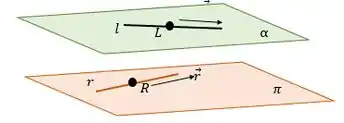
Para determinar um plano temos duas possibilidade: um ponto e seu vetor normal, ouu, dois vetores paralelos ao plano e um ponto. No nosso caso temos a segunda opção, pois temos o vetor diretor da reta que está no plano e além disso o vetor diretor da outra reta é paralelo ao plano, porque o enunciado diz que os planos são paralelos. Assim, com os dois vetores diretores podemos encontrar o vetor normal que será normal à e a . Assim, temos:
Fazendo o produto vetorial entre esses dois vetores obteremos o vetor normal aos planos:
Tendo o vetor normal ao plano e um ponto pertence à ele, determinamos a equação geral dos planos. Começando com o plano que possui o ponto e ,
Portanto,
Fazendo para o plano que possui o ponto e :
Assim,
Passo 3
Portanto,a distância entre os planos é
Passo 4
Para finalizar só falta acharmos o ponto que pertence à e o ponto que pertence à de forma que a reta que é formada por esses dois pontos seja perpendicular às reta e . Então, teremos a seguinte figura:
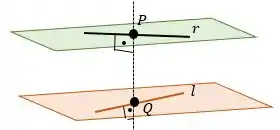
Sabemos que as retas são reversas e vimos na teoria que para achar a distância entre retas reversas precisamos encontrar os ponto e como o enunciado nos pede. Então, vamos primeiro escrever a equação vetorial das retas para então escrevermos os pontos e .
Se pertence à , então:
E pertence à :
Se as retas devem ser perpendiculares à reta formada pelo vetor então, o produto interno entre o vetor e os vetores diretores deve ser ZERO:
Fazendo o produto interno:
Com esses dois produtos internos temos um sisteminha:
Substituindo os valores, temos que:
Substituindo e , achamos e :
Portanto, chegamos onde queríamos:
Resposta
b)
c)
d)