Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Regra dos Retângulos de Riemann

Ver Todos os Exercícios

Teoria

Introdução

Falaaaaaaa aí, tudo certinho? Pois bem... talvez você já tenha estudado esse assunto láaaaaaaaaaaaaaaaaaaaaaaaa em cálculo 1 (sim, já faz um tempinho).

E quando estudamos a teoria de Riemann ainda estávamos descobrindo a importância e o significado das Integrais. Sim, ainda éramos bebês nesse universo das ciências exatas hahahahhahahaha

Mas agora, vamos evoluindo um pouco o raciocínio pra tentar entender para que serve tudo isso.

Basicamente, o Cálculo Numérico serve para criar soluções para problemas utilizando alguns métodos que simplificam a resolução e principalmente que forneça a ferramenta certa para uma máquina resolver o problema.

Tá... mas e daí??

E daí que o método de Riemann é, na verdade, uma das técnicas numéricas que existem para solucionar Integrais. Então, vamos relembrar como isso funciona.

Soma de Riemann

Quando estudamos isso em cálculo, nós vemos também que integral significa a ‘’Área sob a curva”. Muito bem... a teoria de Riemann estuda que abaixo de uma curva qualquer, nós temos a área de n retângulos espaçados por uma amplitude qualquer. A amplitude de cada pedaço tem relação com o máximo e o mínimo valor naquele segmento.

Isso significa que de x 0 até x 1 nós temos um Δ x 1 , e de x 1 até x 2 nós temos um Δ x 2 , até chegar em de x n - 1 até x n nós temos um Δ x n .

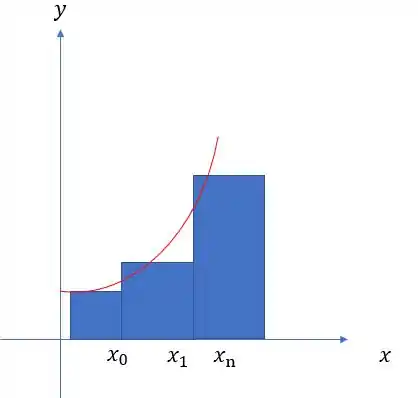
Essa amplitude de pontos com a mesma distância iremos chamar de h , é uma amplitude de um pedaço da subdivisão de uma reta. Veja bem, temos uma reta. Imagine que a cada passo ou pedaço de x no intervalo de x 0   até x n , isso significa que a cada passo temos:

x 0

x 1 = x 0 + h

x n = x n - 1 + h

Para calcular h em um dado intervalo [ a , b ] , nós faremos a diferença entre esse intervalo sobre a quantidade n de retângulos que queremos colocar dentro da nossa curva.

h = b - a n

Quando mais pedaços nós subdividimos o intervalo, menos erros temos influenciando o resultado final. Ouuuuuuuu seja, mais retângulos temos dentro da curva e melhor é a precisão e exatidão do resultado final.

Basicamente, mais retângulos, maior é a partição e menor o erro embutido.

A soma de Riemann é:

∑ i = 1 n f ( c i ) . Δ x i

O resultado final, da área sob a curva, é a soma de caaaaaaaaaaaaaada retângulo dentro da curva. E se considerarmos o intervalo equidistante (o mesmo entre cada segmento). A integração numérica pode ser dada por:

I = h [ f ( x 1 ) + f ( x 2 ) + … + f ( x n ) ]

Sendo o nosso I a área sobre a curva e também o resultado da integral!!!

Passo a passo

Foca nesse passo a passo que é sucesso para resolver a integral:

P a s s o   1 )   C a l c u l a r   o   p a s s o   h   p a r a   n   r e t â n g u l o s   d e n t r o   d a   c u r v a

P a s s o   2 )   M o n t a r   u m a   t a b e l a   c o m   o s   n   v a l o r e s   d e   x 0   a t é   x n   c o m   v a l o r e s   d a s   f u n ç õ e s   a p l i c a d a s .

P a s s o   3 ) M o n t a r   a   i n t e g r a l ,   c o m   o s   v a l o r e s   o b t i d o s :

I R i e m a n n = h [ f ( x 1 ) + f ( x 2 ) + … + f ( x n ) ]

P a s s o   4 )   C a s o   t e n h a   o   v a l o r   r e a l   d a   i n t e g r a l   n o     i n t e r v a l o ,   c a l c u l e   o   e r r o   r e l a t i v o   p e r c e n t u a l :

E R = I r e a l - I R i e m a n n I R i e m a n n

Moleza né?

Bora resolver exercícios!!!

Soma de Riemann

Passo a passo

Exercícios Resolvidos

Exercício Resolvido #1

Material de Cálculo numérico- Uninter

Calcular, pelo método dos retângulos de Riemann pela esquerda e pela direita a seguinte integral com n = 3 :

∫ 0 3 1 1 + x d x

Passo 1

Nosso primeiro passo será calcular o passo h com n = 3 :

h = b - a n = 3 - 0 3 = 1

Logo, nosso passo é h = 1 .

Passo 2

Agora, nós montamos uma tabelinha marota com pontos de 0 até 3 e calcule a função nesses pontos:

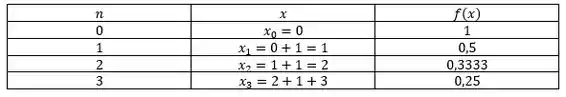
Agora, com esses falores podemos montar a integral pela esquerda e pela direira.

Passo 3

Os passos a esquerda, são os n primeiros valores a esquerda da curva. Ou seja, no intervalo de x 0 até x 2 :

I = h f ( x 0 + f ( x 1 ) + f ( x 2 ) ]

I = 1 1 + 0,5 + 0,333 = 1,833

Passo 4

Os passos a direita, são os n primeiros valores a direita da curva. Ou seja, no intervalo de x 1 até x 3 :

I = h [ f ( x 1 ) + f ( x 2 ) + f ( x 3 ) ]

I = 1 0,5 + 0,333 + 0,25 = 1 , 08 3

Resposta

Esquerda: I = 1,833

Direita: I = 1 , 0 83

Exercício Resolvido #2

Adaptado de “Relembrando Soma de Riemann CNUM-022”

Com n = 2 calcule a Integral abaixo pelo método das somas de Riemann e seu Erro relativo, em relação ao valor original da função:

∫ 1 2 x 2 d x = 2,333

Passo 1

A primeira coisa que fazer é calcular o passo h :

h = 2 - 1 2 = 0,5

Passo 2

Agora, calculamos os valores de pontos com o intervalo dado e as funções nesses pontos:

Passo 3

Com esses valores, calculares o valor da Integral de Riemann à esquerda (apenas por convenção):

I = h f ( x 0 + f ( x 1 ) ]

I = 0,5 [ 1 + 2,25 ]

I = 1,625

Passo 4

Agora, fazemos a comparação do valor obtido com n = 2 e o valor real da função no intervalo.

Sendo a integral e seu valor real:

I r e a l = ∫ 1 2 x 2 d x = 2,333

I R i e m a n n   = 1,625

E R = 2,333 - 1,625 2,333 * 100 = 30,35 %

Resposta

I = 1,625

E R = 30,35 %

Exercício Resolvido #3

Adaptado de “Relembrando Soma de Riemann CNUM-022”

Com n = 4 calcule a Integral abaixo pelo método das somas de Riemann e seu Erro relativo, em relação ao valor original da função. Observe que a função é exatamente a mesma do exercício anterior, e aqui mudamos apenas o valor n , então, compare os resultados obtidos:

∫ 1 2 x 2 d x = 2,333

Passo 1

A primeira coisa que fazer é calcular o passo h :

h = 2 - 1 4 = 0,25

Passo 2

Agora, calculamos os valores de pontos com o intervalo dado e as funções nesses pontos:

Passo 3

Com esses valores, calculares o valor da Integral de Riemann à esquerda (apenas por convenção):

I = h f ( x 0 + f ( x 1 ) + f ( x 2 ) + f ( x 3 ) ]

I = 0,25 [ 1 + 1,5625 + 2,25 + 3,0625 ]

I = 1,9594

Passo 4

Agora, fazemos a comparação do valor obtido com n = 4 e o valor real da função no intervalo.

Sendo a integral e seu valor real:

I r e a l = ∫ 1 2 x 2 d x = 2,333

I R i e m a n n   = 1,9594

E R = 2,333 - 1,9594 2,333 * 100 = 16 %

Comparativamente com n = 2   o erro foi 30,35 % e com n = 4 o erro foi de 16 % , quanto mais subdivisões n tivermos, menor será o erro.

Resposta

I = 1,9594

E R = 16 %

Exercício Resolvido #4

Autoria do Responde Aí

Calcule a integral abaixo com n = 6 e compare com o valor real da integral dentro do intervalo dado:

∫ 0 1 7 x 5 d x = 1,1667

Passo 1

A primeira coisa que fazer é calcular o passo h :

h = 1 - 0 6 = 0,1667

Passo 2

Agora, calculamos os valores de pontos com o intervalo dado e as funções nesses pontos:

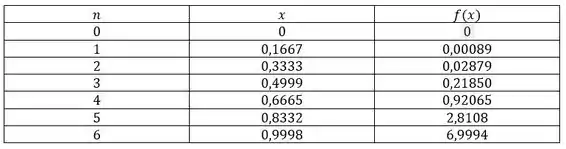
Passo 3

Faremos com o limite a esquerda, por convenção, e por isso não usaremos o valor de 6,9994.

I = h f ( x 0 + f ( x 1 ) + f ( x 2 ) + f ( x 3 ) + f ( x 4 ) + f ( x 5 ) ]

I = 0,1667 [ 0 + 0,00089 + 0,02879 + 0,2185 + 0,92065 + 2,8108 ]

I = 0,6633

Passo 4

Agora, fazemos a comparação do valor obtido com n = 6 e o valor real da função no intervalo.

Sendo a integral e seu valor real:

I R e a l = ∫ 0 1 7 x 5 d x = 1,1667

I R i e m a n n = 0,6633

E R = 1,1667 - 0,6633 1,1667 * 100 = 43 %

Resposta

I R i e m a n n = 0,6633

E R = 43 %

Exercício Resolvido #5

Autoria do Responde Aí

Calcule a integral abaixo com n = 3 e compare com o valor real da integral dentro do intervalo dado:

∫ 0 2 e x d x = 4 , 67 07

Passo 1

A primeira coisa que fazer é calcular o passo h :

h = 2 - 0 3 = 0,6 6 67

Passo 2

Agora, calculamos os valores de pontos com o intervalo dado e as funções nesses pontos:

Passo 3

Faremos com o limite a esquerda, por convenção, e por isso não usaremos o valor de 3,7922.

I = h f ( x 0 + f ( x 1 ) + f ( x 2 ) ]

I = 0 , 6 667 [ 1 + 1,947 + 3,792 ]

I = 4,492

Passo 4

Agora, fazemos a comparação do valor obtido com n = 3 e o valor real da função no intervalo.

Sendo a integral e seu valor real:

∫ 0 2 e x d x = 4,6707

I R i e m a n n = 4,492

E R = 4,6707 - 4,492 4,492 * 100 = 3,8 %

Resposta

I R i e m a n n = 4,492

E R = 3,8 %

Exercícios de Livros Relacionados

8. A regra dos Retângulos repetida é obtida quando aproximamos f ( x ) , em cada subintervalo, por um polinômio de interpolação de grau zero. Encontre a regra dos Retângulos bem como a expressão do er