Interpolação inversa
Teoria
Introdução
Opa, tudo bem. Vamos começar a falar de uma parada mucho loka hehehhehe.
A interpolação inversa serve basicamente para encontrar zeros de funções desconhecidas ... até aí tudo suave né?
A diferença agora é que, além de precisarmos ter váaaaaaaaaaaaaaarios pontos tabelados com nós diferentes , vamos ter que procurar um valor de tal que , sendo valor do contradomínio em um intervalor .
Nós vamos usar uma tal de “tabela inversa” ... Eita, o que que é isso?
O que faremos aqui é inverter os valores, tudo aquilo que era vira, e faz papel de .
E aí nós trabalhamos com a função no modo , que infelizmente, desconhecemos tanto quanto a .
Mas... como se resolve essa coisa? Existem duas abordagens, se liga ai!!
Primeira
Nesse primeiro caso, nós encontramos um polinômio que interpole em e depois achar tal que , sendo necessário achar a raiz do polinômio (por qualquer outro método já estudado para encontrar raízes ).
Segunda
Considerando que é irreversível, pomos interpolar que contém
Considerações gerais para resolução de problemas
Imagine a seguinte tabela:
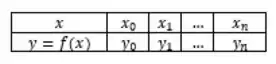
Onde o exercício dá um valor Iremos determinar a raiz dentro do intervalo dado (, de modo que iremos encontrar .
Para resolver o exercício, encontramos:
Um polinômio que interpole nos pontos dados, e com ele achamos a raiz. Nesse caso não teremos estimativa do erro e podemos inverter os valores para usar a interpolação inversa.
Uma condição importante para que uma função contínua (em um intervalo) seja irreversível é que ela seja monótona crescente ou decrescente (ouuuuuu só sobe ou só desce).
Crescente:
Decrescente:
Tranquilo? Bora fazer exercícios que você já vai estar manjando tudo de interpolação inversa!
Primeira
Segunda
Considerações gerais para resolução de problemas
Exercícios Resolvidos
Exercício Resolvido #1
Adaptado de X415 Aplicação de Interpolação Inversa do canal CCL-22
Considere o conjunto de pontos abaixo e encontre um valor , tal que . Resolva encontrando o polinômio interpolador de Lagrange de grau 1:
Passo 1
Aqui, vamos encontrar , tal que
E 2 está dentro do intervalor de que são os pontos que iremos pegar, os demais pontos usaremos só para outros tipos de polinômios!
Por Lagrange:
Considerando
Passo 2
Agora, podemos calcular o nesse polinômio, Vimos que
E :
Resposta
Exercício Resolvido #2
Adaptado de Cálculo Numérico- Interpolação polinomial – Interpolação inversa. Ime-Unicamp Aula 21
Com base no conjunto de pontos abaixo, resolva a interpolação inversa usando a primeira abordagem de resolução do capítulo. Escolha o método que achar necessário para a resolução do polinômio. Além disso, encontre se :
Passo 1
Antes de iniciar a resolução do problema, vale atentar que estamos usando calculadoras diferentes e arredondamentos diferentes, o que pode acarretar pequenas divergências no resultado final, mas se chegar próximo ao que calculamos aqui já está bem aceitável!!!
Vamos encontrar um polinômio que interpole em e depois achar tal que , sendo necessário achar a raiz do polinômio (por qualquer outro método já estudado para encontrar raízes ).
Como temos 3 pontos, podemos montar um polinômio de grau 2:
Podemos resolver por eliminação de Gauss, onde:
Utilizando as regrinhas de Eliminação de Gauss iremos substituir a linha 2, visando zerar o termo :
O mesmo processo deve ser feito para a linha 3:
A nova matriz atualizada é:
Agora, devemos zerar o termo !
Passo 2
Faremos o mesmo processo que o usado anteriormente:
Utilizando as regrinhas de Eliminação de Gauss iremos substituir a linha 2, visando zerar o termo :
Usanto retrosubstituição, ficamos com:
O polinômio pode ser construído :
Passo 3
O exercício pede: se
Podemos resolver essa equação de segundo grau por Bhaskara:
Se:
Com essa equação, conseguimos dois valores para :
Temos dois valores para , agora vamos analisar novamente a tabela:
Observe que sabemos o valor de que está dentro do intervalo [1,22114; 1,3499]. Isso significa que o valor requerido de deve estar entre [0,2 ; 0,3]. Com isso, podemos excluir o valor por estar fora do intervalo [0,2 ; 0,3].
Sendo assim para o valor de .
Resposta
o valor de .
Exercício Resolvido #3
Adaptado de Cálculo Numérico- Interpolação polinomial – Interpolação inversa. Ime-Unicamp Aula 21
Com base no conjunto de pontos abaixo, resolva a interpolação inversa usando a segunda abordagem de resolução do capítulo utilizando a inversão de termos e compare com a resolução do exercício anterior. Escolha o método que achar necessário para a resolução do polinômio. Além disso, encontre se :
Passo 1
Antes de iniciar a resolução do problema, vale atentar que estamos usando calculadoras diferentes e arredondamentos diferentes, o que pode acarretar pequenas divergências no resultado final, mas se chegar próximo ao que calculamos aqui já está bem aceitável!!!
O primeiro passo para resolver esse exercício é inverter as colunas, tudo aquilo que é passa a ser :
Agora, ficamos com :
Passo 2
Com base nesse conjunto de pontos, podemos montar a tabela de diferenças divididas e montar o polinômio interpolador, utilizando o método de Newton:
Com esses valores grifados, podemos montar o polinômio interpolador de ordem 2 em função de :
Se:
Se :
Quando o valor de
Passo 3
Comparando com a resolução do método anterior, essa maneira se torna menos trabalhosa e fornece o resultado correto com menos esforço, apesar da diferença de 0,0002 entre eles.
Resposta
o valor de
Exercício Resolvido #4
Material de Análise numérica da professora Rosália Rodrigues e Antônio Pereira.
Com base no conjunto de pontos abaixo, resolva a interpolação inversa usando a segunda abordagem de resolução do capítulo utilizando a inversão de termos, encontre o valor de quando :
Passo 1
O primeiro passo é trocar os valores de por :
Passo 2
Com base nesse conjunto de pontos, podemos montar a tabela de diferenças divididas e montar o polinômio interpolador, utilizando o método de Newton:
Agora, ficamos com :
Passo 3
O polinômio interpolador passa a ser:
Se:
Se
Resposta
0 o valor de
Exercício Resolvido #5
Autoria do Responde Aí, com base no conteúdo de Ime-Unicamp aula 21
Para retomar o conteúdo, marque V para verdadeiro, e F para falso:
( ) Se ) for irreversível num intervalo contendo , então podemos determinar o polinômio qn que interpola em e definimos .
( ) A função deve ser contínua e reversível.
( ) Dado contínua em , então será monótona crescente se e descrescente se .
Passo 1
( V ) Se ) for irreversível num intervalo contendo , então podemos determinar o polinômio qn que interpola em e definimos .
Passo 2
( F ) A função deve ser contínua e reversível.
A função deve ser contínua e IRREVERSÍVEL no intervalo dado.
Passo 3
( F ) Dado contínua em , então será monótona crescente se e descrescente se .
A monótona crescente é: .
A monótona descrescente é:
Resposta
( V )
( F )
( V )