Mínimos Quadrados
Teoria
Introdução
Fala aí, tudo tranquilo? Vamos começar mais um assuntinho de cálculo numérico. Ainda na vibe das interpolações, de obter um conjunto de pontos que se aproxima do valor real de uma função e essas coisas todas que já estamos carecas de saber.
Veja bem, nós vimos até agora que muitos experimentos geram uma série de dados, esses dados costumam ser rearrumados e organizados pra criar um modelo, um padrão. Muitas das vezes, os erros existentes nesse processo podem afetar e MUITO a sua qualidade.
Um exemplinho disso, é que grande parte dos teoremas físicos (credo), químicos, biológicos surgiram porque alguém ficou aí testando, atéeeeeee criar um modelito que seguisse um padrão! Imagine só a trabalheira que deve ter dado para descobrir a relação lá da elétrica de .
Veja só, esses malucos (no bom sentido, é claro) encontraram uma função matemática que representasse bem os dados obtidos.
Geralmente, nós não usamos interpolação polinomial quando queremos um valor que está fora do intervalo [a,b], ouuuuuu seja, quando queremos extrapolar! Beleza?!
Pensa comigo, qual é o nosso objetivo: achar uma função que se “aproxime bem” e que nos permita extrapolar com uma certa margem de segurança. Já tá ligado em qual método vamos usar??
O método dos mínimos quadrados é MUITO usado para ajustar pontos e melhor aproximar uma função, essa melhor aproximação pode ser polinomial, exponencial, logarítmica, trigonométrica e etc.
Mínimos Quadrados
Veja bem, nós temos uma que nos dá o valor exato da função em um determinado ponto, certo? Aqui, nós queremos obter uma função de aproximação de modo que ela nos forneça valores aproximados e estimados naquele mesmo ponto, e que tenha um erro pequeno. Então, bora entender?
O que vamos fazer é o seguinte: vamos ter uma porrada de pontos (vamos chamar de pontos) de em uma tabela contidos em um intervalo .Podemos ter uma disposição de pontos assim:
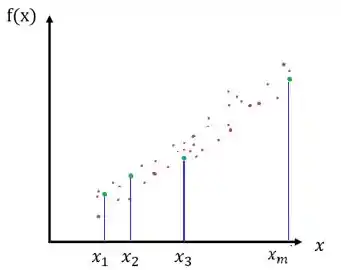
Analisando os pontos e a disposição de e de , e se comporta como uma reta, o que significa que ela forma um polinômio de grau 1. Então:
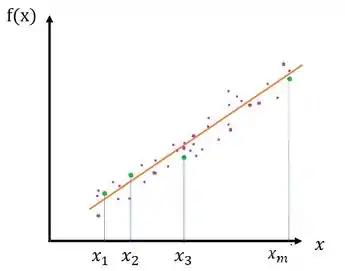
O grande problema de ajuste de curvas, é encontrar funções de modo que cada ponto seja mínimo e definido por:
E essa função se aproxima ao máximo de O método consiste em escolhermos funções contínuas em e obter constantes .
Duas coisas importantes até agora. Primeiro que , onde é o número de funções e é o número de pontos. Segundo que as funções podem ser não lineares (como já disse, podem ser exponenciais e etc), mas relaxa aí que o método para achar os coeficientes é linear haha.
Mas, como eu, um mero mortal vou escolher a melhor função que se aproxima de e melhor ainda, como é que eu vou definir ?
Geralmente, essa escolha é bem visual, nós olhamos um tal de diagrama de dispersão (tipo o gráfico com váaarios pontos que vimos ali em cima) e com ele vemos a curva que melhor se encaixa com os dados.
Vamos falar então do caso mais simples que é através de uma função linear do tipo:
Com o objetivo de determinar valores de e que minimizem os desvios.
Já vimos como o , vendo que era uma reta e obedecia a equação de . A questão agora é como determinar os coeficientes para terminar de encontrar .
Pra cada ponto teremos uma aproximação . Como queremos uma aproximação mais próxima do real, é natural querermos que o módulo da diferença , ou seja, a diferença entre o valor real e o aproximado seja o menor possível (chamamos essa diferença aí de desvio). Observação: calculamos o módulo da diferença porque teremos pontos acima e abaixo da nossa aproximação (só olhar o gráfico anterior, por exemplo), logo, se não colocássemos o módulo, teriam diferenças entre a função real e a aproximada positivas e negativas, anulando umas as outras.
Mas, como o módulo é um pé no saco pra se trabalhar, esse método arrumou uma saída mais inteligente: ele busca o valor mínimo da soma dos quadrados das diferenças entre a função e a aproximação. Eita, ficou confuso? Faz o seguinte:
Pega os desvios em cada um dos pontos da tabela e eleva ao quadrado, porque assim só se apresentam valores positivos. Depois soma a bagaça toda. É esse valor aí que o método minimiza:
Definimos e .
Fazendo aquela história de derivar e igualar a zero vamos acabar chegando no sistema abaixo:
Que é um sistema (lembrando que temos funções ). E temos que:
Onde é o produto escalar de por e a matriz (matriz que apresenta os valores ) é simétrica.
Outra característica interessante de é que se as funções forem ortogonais entre si, nossa matriz não só é simétrica, mas também é diagonal. Como não é o foco desse curso, não vamos entrar no assunto de como descobrir se as funções são ortogonais, mas pode dar uma olhada lá no nosso material de Álgebra se ficou curioso!
Vamos resolver um exemplo pra ficar mais claro? A nossa função é tabelada pelos seguintes pontos:
Plotando esses pontos em um gráfico, temos:
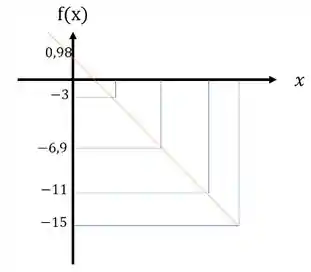
Temos que o gráfico tem comportamento linear. Como o método dos mínimos quadrados, podemos usar aquele polinômio pra funções lineares, que é o que melhor se encaixa:
Antes que a gente comece a pirar com fórmulas, vou ensinar uma tabela que vai ser o auge de cálculo numérico! Primeiro vamos calcular o valor da função em cada ponto . Até ai tudo bem, outro valor que precisamos e também , em CADA ponto dado E láaaaa embaixo da tabela teremos uma linha com o somatório de cada coisa.
Fica assim:
A primeira e segunda coluna são basicamente o que o exercício dá, então é só preencher e . Para cada linha da tabela iremos preencher também cada valor de elevado ao quadrado, e também cada valor de multiplicando pelo valor da função no ponto. Pra fazer o somatório, basta somar os valores totais de caaaaaada coluna.
Obs.: Essa é uma tabela pensando num polinômio de grau 1.
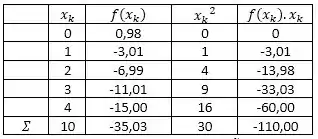
Tabelinha montada, podemos usar aquele sistema de equações de um jeitinho diferente, e se reorganizar direitinho fica com essa cara aqui:
Esse está representando a quantidade de pontos, ok?
Fazendo a multiplicação das matrizes e reorganizando direitinho, as fórmulas para são:
Jogando na fórmulinha aqueles valores que nós organizamos na tabela fica:
Agora só jogamos na fórmula do modelo:
A e uma última coisa, se te perguntarem o erro, é só pegar esse somatório aqui:
Você pega o valor da função em cada ponto e o valor de em cada ponto.
Que foi o que o método minimizou.
Para conferir a eficiência desse método, olha como ficaram os pontos em relação à função que encontramos:
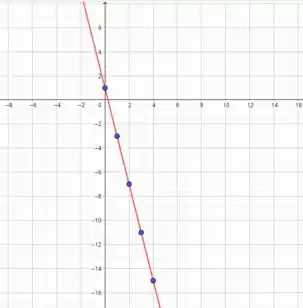
Em azul temos os pontos dados pelo problema e em vermelho temos a equação da reta que calculamos .
Show? Vamos dar uma olhada no algoritmo dessa joça então!
Algoritmo
Passo 1. Dados iniciais (o que seu programa vai receber de você):
a. Vetor de valores
b. Matriz com os vetores
Passo 2. Definimos como uma matriz cheia de zeros.
Passo 3. Definimos como um vetor de tamanho cheio de zeros.
Passo 4. Para de a repita o passo 5.
Passo 5. Para de a repita o passo 6.
Passo 6.
Passo 7. Para de a repita o passo 8.
Passo 8.
Passo 9. Jogamos nossa matriz e nosso vetor em algum método de resolução linear e teremos como retorno o vetor dos coeficientes .
Outro algoritmo importante que deve ser implementado é o do produto escalar. Ele é bem simples de ser implementado e muitas linguagens inclusive contam com bibliotecas com esse método já pronto para uso.
Por fim, para garantir que ninguém faça besteira com seu programa (isso inclui você mesmo haha) é interessante adicionarmos algumas medidas de segurança. Por exemplo, precisamos que e que os vetores tenham elementos cada. Isso impede que seu programa dê o algum problema se algum valor errado for imputado sem querer.
Algoritmo
Exercícios Resolvidos
Exercício Resolvido #1
Lista 5 – Professora Angela – UFRJ – Questão 2
Dada a tabela:
Calcular usando regressão linear.
Passo 1
Bom, esse é um exercício inicial de mínimos quadrados, bem tranquilo né? A dificuldade vai aumentando nos outros exercícios. Bora resolver essa bagaça!!
Regressão linear é simplesmente a aproximação por mínimos quadrados usando uma reta. Então:
Logo, e .
Temos então os vetores:
Então podemos montar essa tabelinha aqui:
Passo 2
Agora montamos a matriz que vai ser já que temos duas funções :
Ou seja, para , multiplicamos o vetor por ele mesmo e somamos os resultados:
Em , multiplicamos o vetor pelo vetor e somamos os resultados e assim por diante. Chegando na matriz .
E o vetor :
O raciocínio na montagem da matriz é o mesmo da montagem de , ou seja, em , multiplicamos pelo e somamos os resultados e em , multiplicamos por e somamos os resultados, chegando na matriz .
Passo 3
Temos que resolver o sistema:
Então, fazendo a multiplicação das matrizes:
Resolvendo esse sistema, chegamos a:
Com isso, chegamos a:
Aproximando o valor pedido:
Resposta
Exercício Resolvido #2
Lista 6 – UNICAMP – Questão 2
Encontre polinômios de grau , e que minimizam o resíduo na aproximação dos dados da tabela abaixo. Qual deles proporcionou um melhor resultado?
Passo 1
Primeira pergunta, o que é esse resíduo? Bom isso aí é só outro nome para aquela soma dos desvios ao quadrado:
Passo 2
Vamos começar com o polinômio de primeiro grau! Temos:
Logo, e .
Temos então os vetores:
Passo 3
Agora montamos a matriz que vai ser já que temos duas funções :
E o vetor :
Resolvendo o sistema:
Com isso, chegamos a:
Passo 4
Agora vamos calcular o resíduo! Vamos montar uma outra tabelinha pra ajudar a gente:
Então nosso resíduo foi .
Passo 5
Agora o polinômio de segundo grau:
Logo, , e .
Temos então os vetores:
Passo 6
Agora montamos a matriz que vai ser já que temos três funções :
E o vetor :
Resolvendo o sistema:
Com isso, chegamos a:
Passo 7
Agora vamos calcular o resíduo! Vamos montar aquela mesma tabelinha pra ajudar a gente:
Então nosso resíduo foi .
Passo 8
Por fim, o polinômio de terceiro grau:
Logo, , , e .
Temos então os vetores:
Passo 9
Agora montamos a matriz que vai ser dessa vez já que temos quatro funções . Ô sisteminha chato que vai ficar esse em!
E o vetor :
Resolvendo o sistema (coragem):
Com isso, chegamos a:
Passo 10
Pra encerrar vamos calcular o resíduo montando a tabela:
Então nosso resíduo foi .
Passo 11
Agora comparamos os resíduos:
Polinômio de grau :
Polinômio de grau :
Polinômio de grau :
O que proporcionou o melhor resultado foi o que teve menor resíduo, o de grau .
Novamente o exercício não pediu isso, mas se liga em como ficaram as curvas:
A azul contínua é o polinômio de grau . A verde pontilhada é o polinômio de grau . A laranja tracejada é o polinômio de grau .
Resposta
Grau 1:
Resíduo:
Grau 2:
Resíduo:
Grau 3:
Resíduo:
O polinômio de grau proporcionou o melhor resultado.
Exercício Resolvido #3
Lista 4 – Professor Mauro – UFRJ – Questão 9a
A tabela abaixo representa o número oficial aproximado de pessoas com dengue, ou seja, infectados pelo mosquito Aedes aegypti no Rio de Janeiro:
Os dados relativos correspondem ao número de casos registrados nos meses de janeiro e fevereiro.
Usando uma reta, estime o número de infectados no mês de março de , pelo método dos mínimos quadrados.
Passo 1
A primeira coisa que temos que perceber é que a tabela trata de horizontes de tempo diferentes. Começa de ano a ano e depois passa a funcionar de mês a mês.
Como estamos querendo estimar o número de casos em um mês de só faz sentido considerarmos os dois últimos pontos da tabela que também tratam de mês. Então ficamos só com:
E como o enunciado pede para estimarmos usando uma reta:
Logo, e . Temos então que:
Passo 2
Agora montamos a matriz que vai ser :
E o vetor :
Resolvendo o sistema:
Com isso, chegamos a:
Passo 3
Aproximando para o terceiro mês, temos:
Então nossa estimativa é de infectados no mês de março.
Resposta
infectados no mês de março de .
Exercício Resolvido #4
Márcia A. Gomes Ruggiero e Vera Lúcia da Rocha Lopes, Cálculo Numérico – Aspectos Teóricos e Computacionais, 2ª ed. São Paulo: MAKRON Books, 1996, pag 287, exercício 2
Ajuste os dados abaixo pelo método dos mínimos quadrados utilizando:
Uma reta
Uma parábola do tipo
Trace as duas curvas no gráfico de dispersão dos dados. Como você compararia as duas curvas com relação aos dados?
Passo 1
Queremos aproximar a função para uma reta, então o polinômio interpolador será do tipo:
Sabemos que o polinômio será do tipo:
Logo comparando as duas equações concluímos que : e .
Vamos construir os vetores:
- será o vetor com todos os valores de x:
- será o vetor constante pois:
- será o vetor com todos os valores de y:
-
-
-
-
- será o vetor com todos os valores de x² pois :
- será o vetor com valores de x pois:
- será o vetor constante pois:
- será o vetor com todos os valores de y:
Passo 2
Precisamos resolver o seguinte sistema:
Sendo a matriz , que vai ser já que temos duas funções , como:
E o vetor :
Vamos calcular o termos da matriz A:
Então a matriz é:
Fazendo as mesmas contas do produto escalar agora para a matriz B, obtemos:
Obtemos agora o sistema:
Que nos dá as seguintes equações:
Isolando da segunda equação obtemos:
Substituindo na primeira equação podemos encontrar o valor de e consequentemente :
Com isso, chegamos a resposta:
Passo 3
Agora queremos aproximar para uma parábola, então o polinômio será do tipo:
Sabemos que o polinômio será do tipo:
Logo comparando as duas equações concluímos que :, e .
Temos então os vetores:
Passo 2
Precisamos resolver o seguinte sistema:
Sendo a matriz :
E o vetor :
Calculando os termos da matriz A temos:
O mesmo para o vetor B:
Obtemos o sistema:
Onde obtemos as seguintes equações:
Resolvendo o sistema obtemos:
Com isso, chegamos a:
Passo 3
Traçando as duas curvas no gráfico de dispersão temos:
Quando fazemos esse tipo de aproximação, sempre há um erro, se calcularmos qual aproximação tem o melhor erro podemos compará-las. O de resíduo é justamente o erro entre os pontos conhecidos da função e o polinômio interpolador, e é calculado por:
E a mesma fórmula tanto para a reta e para a parábola.
Vamos montar uma tabelinha para cada caso pra ficar mais fácil. Quem tiver a menor soma de resíduos será a melhor interpolação.
Para a reta temos:
E para a parábola:
Logo, temos que o resíduo da parábola é menor, então ela é uma aproximação melhor.
Resposta
A parábola é a melhor aproximação pois tem um resíduo de enquanto a reta tem um resíduo de .
Exercício Resolvido #5
Márcia A. Gomes Ruggiero e Vera Lúcia da Rocha Lopes, Cálculo Numérico – Aspectos Teóricos e Computacionais, 2ª ed. São Paulo: MAKRON Books, 1996, pag 288, exercício 3
Dada a tabela abaixo, faça o gráfico de dispersão dos dados e ajuste uma curva da melhor maneira possível:
Passo 1
O nosso gráfico de dispersão vai ficar assim:
O enunciado não especificou que tipo de curva ele quer, só disse para ajustá-la da melhor forma possível. Pra mim esse gráfico ta lembrando bastante o de né? Bom, então vamos usar como a função o seguinte:
Logo, e .
Passo 2
Temos então os vetores:
Agora montamos a matriz que vai ser já que temos duas funções :
E o vetor :
Resolvendo o sistema:
Passo 3
Com isso, chegamos a:
O exercício não pediu isso, mas tomei a liberdade de traçar a curva que calculamos em cima do gráfico de dispersão e olha como ficou:
Eu diria que foi uma aproximação excelente haha.
Resposta
Exercício Resolvido #6
Lista de Exercícios - FEI
Numa pesquisa da Secretaria da Saúde coletou-se N de pessoas infectadas pelo vírus H1N1 num tempo t dado pela tabela abaixo. Admitindo-se que uma reta ajusta os dados da tabela, quantas pessoas estarão infectadas no 2º dia?
Passo 1
Fala aí, vc decidiu fazer engenharia né? Que que vc tem a ver com H1N1, mas vamo lá né?!
O professor tá pedindo pra ajustarmos a tabela por uma reta, então
Agora precisamos descobrir esses coeficientes e .
A função que acompanha chamaremos de e nesse caso . Podemos dizer também que está sendo multiplicado por
Passo 2
Agora vamos montar a tabela que vai ajudar pacas a aplicar o método
Se liga, a primeira coluna é do , como , basta repetir os valores de dá tabela que o professor deu.
A segunda é a coluna de , e ele é igual a 1. Na última coluna colocamos os valores de diretinho da tabela que o professor deu.
Passo 3
Para achar os coeficientes e vamos fazer o seguinte óh:
Para achar basta multiplicar cada elemento da primeira coluna por ele mesmo e depois soma-los.
Agora vamos achar ou , pra isso é só multiplicar a primeira coluna pela segunda e somar
Para acharmos é a mesma idéia, só multiplicar os valores da coluna por ela mesma e somar.
Colocando na tabela temos:
Agora basta achar e , para isso vamos seguir a mesma ideia de multiplicar elemento a elemento as colunas e somar todo mundo.
Passo 4
Se vc já sacou, essa parte de baixo de baixo é um sistema, Ax=b com ele a gente vai encontrar os coeficientes e
Agora é só resolver o sistema né!!!
Então
Passo 5
Como o professor quer saber pro 2º dia, basta substituir t=2
Resposta
5.5 milhares de pessoas
Exercício Resolvido #7
Livro Cálculo Numérico – Álvaro Puga Paz – LCTE Editora
Ajustar os dados da tabela abaixo por um polinômio do 2º grau completo.
Passo 1
O professor tá pedindo pra ajustarmos a tabela por um polinômio do 2º grau, então
As funções que multiplicam , , são , e como não temos “nada” ao lado do , podemos dizer também que ele está sendo multiplicado por
Agora precisamos descobrir esses coeficientes , e .
Passo 2
Agora vamos montar a tabela que vai ajudar pacas a aplicar o método.
As colunas e da direita são apenas uma cópia da tabela que o professor deu, blz?
E nas outras 3 colunas a gente coloca as funções que estão multiplicando os coeficientes , e .
A coluna , basta preencher com 1’s. Já a coluna , vai ser preenchida com os valores de , diretinho da tabela que o professor deu. E por último a coluna , será preenchida com os valores de da tabela que o professor deu elevando um a um ao quadrado. Fechow??
Ela vai ficar assim:
Passo 3
Para achar os coeficientes , e vamos fazer o seguinte óh:
Calma, calma é feio, mas é tranquilo de fazer.
Para achar basta multiplicar cada elemento da primeira coluna por ele mesmo e depois soma-los.
Agora vamos achar ou (sim, eles são iguais), pra isso é só multiplicar a primeira coluna pela segunda e somar
Bora achar agora ou (eles também são iguais), pra isso é só multiplicar a primeira coluna pela terceira e somar
Para acharmos é a mesma idéia, só multiplicar os valores da coluna por ela mesma e somar.
Calma tá acabando
Para achar ou (eles também são iguais), pra isso é só multiplicar a segunda coluna pela terceira e somar
E pela última vez, para achar basta multiplicar os valores da coluna por ela mesma e somar.
Uffaaaa! Colocando na tabela temos:
Beleeeeza!!, faltou só multiplicar cada coluna pela coluna do e somar depois. Boora lá!
Passo 4
Se vc já sacou, essa parte de baixo de baixo é um sistema, Ax=b com ele a gente vai encontrar os coeficientes , e
Agora é só resolver o sistema né!!!
Então
Resposta
Exercício Resolvido #8
Livro Cálculo Numérico – Álvaro Puga Paz – LCTE Editora
A tabela abaixo refere-se à potência P (em hp), de um motor Diesel, em função do número de rotações r (em rpm). Pede-se:
Ajustar os dados da tabela por uma reta. Qual a potência para 800 rpm?
Passo 1
O professor tá pedindo pra ajustarmos a tabela por um polinômio do 1º grau, então
As funções que multiplicam e são , e como não temos “nada” ao lado do , podemos dizer também que ele está sendo multiplicado por
Agora precisamos descobrir esses coeficientes e
Passo 2
Agora vamos montar a tabela que vai ajudar pacas a aplicar o método.
As colunas e r da direita são apenas uma cópia da tabela que o professor deu, blz?
E nas outras 2 colunas a gente coloca as funções que estão multiplicando os coeficientes e .
A coluna , basta preencher com 1’s. Já a coluna , vai ser preenchida com os valores de , diretinho da tabela que o professor deu. Fechow??
Ela vai ficar assim:
Passo 3
Para achar os coeficientes e como que faz?? Vamo dar uma extendida na nossa tabela.
Não surta, que vai ser de boas...calma aeew!
Para achar basta multiplicar cada elemento da primeira coluna por ele mesmo e depois soma-los.
Agora vamos achar ou (sim, eles são iguais), pra isso é só multiplicar a primeira coluna pela segunda e somar
Para acharmos é a mesma idéia, só multiplicar os valores da coluna por ela mesma e somar.
Calma tá acabando
Faltou só multiplicar cada coluna pela coluna do e somar depois. Boora lá!
Uffaaaa! Colocando na tabela temos:
Passo 4
Se vc já sacou, essa parte de baixo de baixo é um sistema, Ax=b com ele a gente vai encontrar os coeficientes e .
Agora é só resolver o sistema né!!!
Então
Beleeeza, já achamos a reta. Agora precisamos achar a potência para 800 rpm
Passo 5
Pra isso basta substituir na reta que a gente achou!