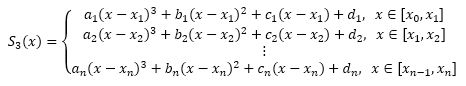Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Spline Cúbica Interpolante

Ver Todos os Exercícios

Teoria

Introdução

Faaaaaaaaala meu consagrado, nós vimos até agora algumas técnicas pra encontrar a solução de uma função e até mesmo uma função alternativa e aproximada que chegue bem perto da função real em um dado intervalo. E principalmente vimos o que é uma Spline interpolante de grau 1, mas em alguns casos a spline de grau não é tão usada, então vamos seguir em frente para a Spline Cúbica.

Veja bem, quando montamos e olhamos as funções em gráfico (junto com a função real), percebemos que forma um graaaaande “zigue-zague”, isso acontece porque para resolver a função fazemos vários subintervalos s p x .

O grande problema é que essas splines lineares formam essas “quinas” entre os nós. Se tu relembrar um pouquinho lá do cálculo 1, a derivada primeira é descontínua nesses nós, e pode causar uns probleminhas dependendo do que vamos fazer com o polinômio interpolador.

Mas relaxa que pra tudo tem-se um jeitinho.

E é por esse motivo que as splines cúbicas são muito mais usadas! Hmmm ... você deve estar pensando, e não tem splines quadráticas?

Veja bem, é uma perguntinha importante porque usando spline quadrática teremos derivadas contínuas de primeira ordem, mas não de segunda ordem! E isso pode acabar sendo um problema já que a concavidade da função pode ficar trocando a cada nó (lembre-se que o sinal da derivada segunda define a concavidade da nossa função).

Pensando nisso a nossa S 3 x tem derivadas de ordem 1 e 2 contínuas fazendo dela uma função bonitinha sem quinas nem mudanças de concavidade nos nós. Bora ver como definimos essas Splines?

Spline Cúbica Interpolante

Relembrando aqui: temos uma função f x tabelada em n + 1 pontos, nossa Spline Cúbica Interpolante S 3 x é definida assim:

S 3 x = s 1 x ,       x ∈ x 0 , x 1 s 2 x ,       x ∈ x 1 , x 2 ⋮ s n x ,       x ∈ x n - 1 , x n

Onde nós podemos supor que a nossa f x é tabelada em pontos de Supondo que f(x) esteja tabelada nos pontos x i , i = 0, 1, 2, ..., n a função S 3 x é chamada spline cúbica interpolante de f x nos nós x i , i = 0, ..., n. Entãaaao:

1. S 3 x i = f x i ,   p a r a   i = 0,1 , … , n

2. s k x = a k x - x k 3 + b k x - x k 2 + c k x - x k + d k ,   p a r a   k = 1,2 , … , n

3. s k x k = s k + 1 x k ,   p a r a   k = 1,2 , … , n - 1

4. s k ' x k = s k + 1 ' x k ,   p a r a   k = 1,2 , … , n - 1

5. s k ' ' x k = s k + 1 ' ' x k ,   p a r a   k = 1,2 , … , n - 1

Ahhhh claro, mas, pra que raios vou usar isso? Retomando um pouquinho, a spline cúbica é bem parecida com a linear, dividida em intervalos e tal, maaaas, as condições mudam assim:

1. Devemos ter n+1 condições pra que S 3 x interpole f x nos nós x 0 , x 1 , … , x n .

2. Nessa a gente simplesmente define que as funções que interpolam cada intervalo s k x são cúbicas.

3. A função é contínua, ou seja, as funções s k x sempre se encontram nos extremos de seus intervalos de interpolação.

4. A derivada primeira da função é contínua, ou seja, a derivada primeira das funções s k x sempre são iguais nos extremos de seus intervalos de interpolação. Isso garante que não haverá quinas nos nós de interpolação.

5. A derivada segunda da função é contínua, ou seja, a derivada segunda das funções s k x sempre são iguais nos extremos de seus intervalos de interpolação. Isso garante que o gráfico não trocará de concavidade abruptamente nos nós de interpolação.

Ficou mais claro agora? Basicamente o que você tem que fazer é pegar a nossa s k x e fazer ela valer pra todas as condições em cada subintervalo. O que no caso dá um trabalho desgraçado para não dizer outra coisa, então eu vou te dar a fórmula direto! ;)

O que você precisa saber é o seguinte. Para cada s k x temos 4 incógnitas a k , b k , c k , d k . Ou seja, nossa função S 3 x tem 4 incógnitas por equação e n equações, o que nos leva a 4 n incógnitas.

O problema é que todas aquelas condições que a gente definiu só nos dão 4 n - 2 condições, deixando duas em aberto! É aí que a nossa Spline cúbica se divide (sim, ainda tem mais)! Vamos ver quais são as condições mais comuns de se usar:

Spline Cúbica Natural

Nesse caso, nós aproximamos que os polinômios cúbicos são aproximadamente lineares nos extremos dos intervalos, de forma que:

S ' ' x 0 = S ' ' x n = 0

Juntando essas duas condições com as outras e definindo h j = x j - x j - 1 , chegamos no sistema n + 1 × n + 1 :

A x = b ,

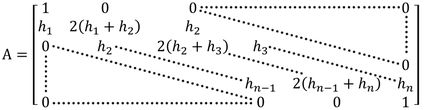
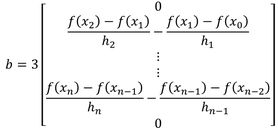
E isso só nos dá os coeficientes b k . Lembrando que só vamos usar o b 1 até o b n na nossa função spline. O b 0 serve para encontrarmos os outros coeficientes:

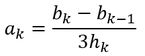
Fórmulas bem chatinhas né? Bom, mas a menos que esteja a fim de deduzir tudo na hora da prova (acredite, você não vai estar afim haha) vai ter que gravar mesmo. Vamos ver um exemplo. Encontre uma aproximação para f 0.75 por spline cúbica natural da tabela abaixo:

Lembrando que h j = x j - x j - 1 e definindo:

x 0 = 0 ; x 1 = 0.5 ; x 2 = 1.0 ; x 3 = 1.5 ; x 4 = 2.0

Temos nossa matriz A . Normalmente eu preencho ela da seguinte forma. Eu monto uma matriz n + 1 × n + 1 . Nesse caso 5 × 5 e completo a primeira e última linha:

  A = 1 0 0 0 0 0 0 0 0 1

Agora logo embaixo do primeiro 1 , botamos h 1 e vamos aumentando o índice na diagonal:

A = 1 0 0 0 0 h 1 h 2 h 3 0 0 0 0 1

Do lado do h 1 eu completo com 2 h 1 + h 2 e também vamos aumentando o índice na diagonal:

A = 1 0 0 0 0 h 1 2 h 1 + h 2 h 2 2 h 2 + h 3 h 3 2 h 3 + h 4 0 0 0 0 1

Agora do lado do 2 h 1 + h 2 completamos com h 2 e novamente aumentamos o índice na diagonal:

A = 1 0 0 0 0 h 1 2 h 1 + h 2 h 2 h 2 2 h 2 + h 3 h 3 h 3 2 h 3 + h 4 h 4 0 0 0 0 1

Por fim, completamos tudo com 0 :

A = 1 0 0 0 0 h 1 2 h 1 + h 2 h 2 0 0 0 h 2 2 h 2 + h 3 h 3 0 0 0 h 3 2 h 3 + h 4 h 4 0 0 0 0 1

Agora é a vez do nosso vetor b . Ele é um vetor n + 1 × 1 . Nesse caso, 5 × 1 . Eu costumo gravar só que a primeira e última linhas são 0 , que tem um 3 multiplicando por fora e que a segunda linha é sempre f x 2 - f x 1 h 2 - f x 1 - f x 0 h 1 . Aí para as outras linhas é só ir aumentando o índice.

b = g 0 g 1 g 2 g 3 g 4 = 3 0 f x 2 - f x 1 h 2 - f x 1 - f x 0 h 1 f x 3 - f x 2 h 3 - f x 2 - f x 1 h 2 f x 4 - f x 3 h 4 - f x 3 - f x 2 h 3 0

Beleza, agora vamos encontrar nossos h j . Como os pontos são igualmente espaçados:

h 1 = h 2 = h 3 = h 4 = 0.5

E resolvendo os termos de b :

3 f x 2 - f x 1 h 2 - f x 1 - f x 0 h 1 = - 11.046

3 f x 3 - f x 2 h 3 - f x 2 - f x 1 h 2 = - 4.425

3 f x 4 - f x 3 h 4 - f x 3 - f x 2 h 3 = - 4.0818

Ficamos então com o sistema:

1 0 0 0 0 0.5 2 0.5 0 0 0 0.5 2 0.5 0 0 0 0.5 2 0.5 0 0 0 0 1 b 0 b 1 b 2 b 3 b 4 = 0 - 11.046 - 4.425 - 4.0818 0

Resolvendo por eliminação de Gauss obtemos:

b 0 = 0

b 1 = - 5.4311

b 2 = - 0.3675

b 3 = - 1.949

b 4 = 0

Agora repare que ele pede S 3 0.75 . O ponto x = 0.75 se encontra entre x 1 e x 2 , então só precisamos da função s 2 x :

a 2 = b 2 - b 1 3 h 2 = 3.3758

c 2 = f x 2 - f x 1 h 2 + h 2 2 b 2 + b 1 3 = - 7.1337

d 2 = f x 2 = - 0.8228

Finalmente substituímos na fórmula do s 2 x :

s 2 x = a 2 x - x 2 3 + b 2 x - x 2 2 + c 2 x - x 2 + d 2

s 2 0.75 = 3.3758 - 0.25 3 - 0.3675 - 0.25 2 - 7.1337 - 0.25 - 0.8228

s 2 0.75 = 0.8849

Spline Cúbica Apertada

Essa é a forma mais geral onde nós definimos as derivadas nos extremos do intervalo:

f ' x 0 = m 0

f ' x n = m n

Nesse caso a única coisa que muda são as primeiras linhas de A e de b do sistema A x = b . Aqui teremos:

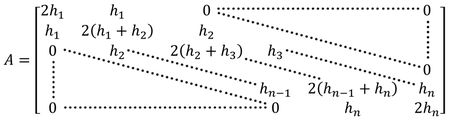
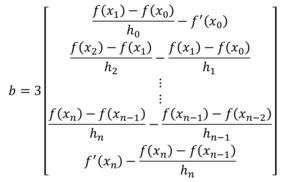
Os outros coeficientes são obtidos da mesma forma:

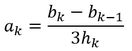
Algoritmo

Spline Cúbica Natural

Passo 1. Dados iniciais (o que seu programa vai receber de você):

a. Vetor de valores x = x 0 , x 1 , … , x n

b. Vetor de valores f x = f x 0 , f x 1 , … , f x n

Passo 2. Para i de 1 a n repita o passo 3.

Passo 3. h i = x i - x i - 1

Passo 4. Para i de 1 a n - 1 repita o passo 5.

Passo 5. g i = 3 f x i + 1 - f x i h i + 1 - f x i - f x i - 1 h i

Passo 6. Definimos A como uma matriz n + 1 × n + 1 cheia de zeros.

Passo 7. A 00 = 1 ; A n n = 1

Passo 8. Para i de 1 a n - 1 repita os passos 9, 10 e 11.

Passo 9. A i i - 1 = h i

Passo 10. A i i = 2 h i + h i + 1

Passo 11. A i i + 1 = h i + 1

Passo 12. Jogamos nossa matriz A e nosso vetor g no algoritmo da eliminação de Gauss retornando x = b 0 , b 1 , … , b n .

Passo 13. Para i de 1 a n repita os passos 14, 15 e 16.

Passo 14. a i = b i - b i - 1 3 h i

Passo 15. c i = f x i - f x i - 1 h i + h i 2 b i + b i - 1 3

Passo 16. d i = f x i

Passo 17. Retorne os conjuntos a i , b i , c i , d i para i de 1 a n .

Com isso, chegamos à nossa S 3 x :

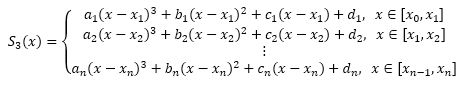
Spline Cúbica Apertada

Passo 1. Dados iniciais (o que seu programa vai receber de você):

a. Vetor de valores x = x 0 , x 1 , … , x n

b. Vetor de valores f x = f x 0 , f x 1 , … , f x n

c. O valor das derivadas nos extremos f ' x 0 = m 0 e f ' x n = m n

Passo 2. Para i de 1 a n repita o passo 3.

Passo 3. h i = x i - x i - 1

Passo 4. Para i de 1 a n - 1 repita o passo 5.

Passo 5. g i = 3 f x i + 1 - f x i h i + 1 - f x i - f x i - 1 h i

Passo 6. g 0 = f x 1 - f x 0 h 0 - f ' x 0

Passo 7. g n = f ' x n - f x n - f x n - 1 h n

Passo 8. Definimos A como uma matriz n + 1 × n + 1 cheia de zeros.

Passo 9. A 00 = 2 h 1 ; A 01 = h 1 ; A n n = 2 h n ; A n n - 1 = h n

Passo 10. Para i de 1 a n - 1 repita os passos 11, 12 e 13.

Passo 11. A i i - 1 = h i

Passo 12. A i i = 2 h i + h i + 1

Passo 13. A i i + 1 = h i + 1

Passo 14. Jogamos nossa matriz A e nosso vetor g no algoritmo da eliminação de Gauss retornando x = b 0 , b 1 , … , b n .

Passo 15. Para i de 1 a n repita os paços 16, 17 e 18.

Passo 16. a i = b i - b i - 1 3 h i

Passo 17. c i = f x i - f x i - 1 h i + h i 2 b i + b i - 1 3

Passo 18. d i = f x i

Passo 19. Retorne os conjuntos a i , b i , c i , d i para i de 1 a n .

Com isso, chegamos à nossa S 3 x :

Spline Cúbica Natural

Spline Cúbica Apertada

Algoritmo

Exercícios Resolvidos

Exercício Resolvido #1

Márcia A. Gomes Ruggiero e Vera Lúcia da Rocha Lopes, Cálculo Numérico – Aspectos Teóricos e Computacionais, 2ª ed. São Paulo: MAKRON Books, 1996, pag 253, exemplo 14

Encontrar uma aproximação para f 0.25 por spline cúbica natural na tabela:

Passo 1

Primeiro definimos:

x 0 = 0 ; x 1 = 0.5 ; x 2 = 1.0 ; x 3 = 1.5 ; x 4 = 2.0

E como o espaçamento entre os pontos é o mesmo, temos h i = h = 0.5 . Substituindo no sistema A x = b :

A = 1 0 0 0 0 h 1 2 h 1 + h 2 h 2 0 0 0 h 2 2 h 2 + h 3 h 3 0 0 0 h 3 2 h 3 + h 4 h 4 0 0 0 0 1 = 1 0 0 0 0 0.5 2 0.5 0 0 0 0.5 2 0.5 0 0 0 0.5 2 0.5 0 0 0 0 1

b = 3 0 f x 2 - f x 1 h 2 - f x 1 - f x 0 h 1 f x 3 - f x 2 h 3 - f x 2 - f x 1 h 3 f x 4 - f x 3 h 4 - f x 3 - f x 2 h 3 0 = 0 - 7.6818 - 7.3374 - 7.2798 0

Passo 2

Resolvemos então o sistema linear:

1 0 0 0 0 0.5 2 0.5 0 0 0 0.5 2 0.5 0 0 0 0.5 2 0.5 0 0 0 0 1 b 0 b 1 b 2 b 3 b 4 = 0 - 7.6818 - 7.3374 - 7.2798 0

E obtemos que:

b 0 b 1 b 2 b 3 b 4 = 0 - 3.327 - 2.055 - 3.126 0

Passo 3

Agora repare que ele pede o valor em x = 0.25 que está entre x 0 e x 1 , logo precisamos do valor de s 1 0.25 .

Aplicando as fórmulas:

a 1 = b 1 - b 0 3 h 1 = - 2.218

c 1 = f x 1 - f x 0 h 1 + h 1 2 b 1 + b 0 3 = - 3.3858

d 1 = f x 1 = 1.8616

Passo 4

Juntando tudo temos:

s 1 x = - 2.218 x - 0.5 3 - 3.327 x - 0.5 2 - 3.3858 x - 0.5 + 1.8616

s 1 0.25 = 2.5348

Resposta

s 1 0.25 = 2.5348

Exercício Resolvido #2

Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 161, exercício 4

Construa a spline cúbica natural para as seguintes tabelas:

Passo 1

a Primeiro definimos:

x 0 = 0 ; x 1 = 0.5

h 1 = 0.5

Substituindo no nosso sistema A x = b :

A = 1 0 0 1

b = 0 0

Repare que como a primeira e última linha de A e de b devem ser zeradas a gente acaba não tendo que fazer conta nenhuma haha.

Resolvendo isso aí temos:

b 0 = 0

b 1 = 0

Jogando na fórmula:

a 1 = b 1 - b 0 3 h 1 = 0

c 1 = f x 1 - f x 0 h 1 + h 1 2 b 1 + b 0 3 = 2.71828 - 1 0.5 = 3.43656

d 1 = f x 1 = 2.71828

Passo 2

Como só temos um intervalo então nossa função será:

S 3 x = s 1 x = 3.43656 x - 0.5 + 2.71828

s 1 x = 1 + 3.43656 x ,   x ∈ 0,0.5

Passo 3

b Definimos:

x 0 = - 0.25 ; x 1 = 0.25

h 1 = 0.5

Substituindo no nosso sistema A x = b :

A = 1 0 0 1

b = 0 0

Resolvendo isso aí temos:

b 0 = 0

b 1 = 0

Jogando na fórmula:

a 1 = b 1 - b 0 3 h 1 = 0

c 1 = f x 1 - f x 0 h 1 + h 1 2 b 1 + b 0 3 = 0.800781 - 1.33203 0.5 = - 1.0625

d 1 = f x 1 = 0.800781

Passo 4

Como só temos um intervalo então nossa função será:

S 3 x = s 1 x = - 1.0625 x - 0.25 + 0.800781

s 1 x = 1.06641 - 1.0625 x ,   x ∈ - 0.25,0.25

Passo 5

c Definimos:

x 0 = 0.1 ; x 1 = 0.2 ; x 2 = 0.3

h 1 = h 2 = h = 0 . 1

Substituindo no nosso sistema A x = b :

A = 1 0 0 h 1 2 h 1 + h 2 h 2 0 0 1 = 1 0 0 0.1 0.4 0.1 0 0 1

b = 0 f x 2 - f x 1 h 2 - f x 1 - f x 0 h 1 0 = 0 0.52575 0

Resolvendo isso aí temos:

b 0 = 0

b 1 = 1.314375

b 2 = 0

Passo 6

Aqui temos dois intervalos. Jogando na fórmula do primeiro:

a 1 = b 1 - b 0 3 h 1 = 4.38125

c 1 = f x 1 - f x 0 h 1 + h 1 2 b 1 + b 0 3 = - 2.6198488

d 1 = f x 1 = - 0.56079734

E para o segundo intervalo:

a 2 = b 2 - b 1 3 h 2 = - 4.38125

c 2 = f x 2 - f x 1 h 2 + h 2 2 b 2 + b 1 3 = - 2.4884113

d 2 = f x 2 = - 0.81401972

Passo 7

Juntando tudo:

S 3 x = s 1 x = 4.38125 x - 0.2 3 + 1.3144 x - 0.2 2 - 2.6198 x - 0.2 - 0.5608 ,       x ∈ 0.1,0.2 s 2 x = - 4.38125 x - 0.3 3 - 2.4884 x - 0.3 - 0.814 ,       x ∈ 0.2,0.3

Passo 8

d Força agora que estamos na última letra! Nessa temos:

x 0 = - 1 ; x 1 = - 0.5 ; x 2 = 0 ; x 3 = 0.5

E todos os h são iguais de novo (para nossa alegria):

h = 0.5

Agora fazemos o de sempre. Substituímos no sistema A x = b :p

A = 1 0 0 0 h 1 2 h 1 + h 2 h 2 0 0 h 2 2 h 2 + h 3 h 3 0 0 0 1 = 1 0 0 0 0.5 2 0.5 0 0 0.5 2 0.5 0 0 0 1

b = 0 f x 2 - f x 1 h 2 - f x 1 - f x 0 h 1 f x 4 - f x 3 h 4 - f x 3 - f x 2 h 3 0 = 0 0.2674 0.33103 0

Resolvendo o sistema chegamos a:

b 0 b 1 b 2 b 3 = 0 0.098476 0.140897 0

Passo 9

Esse vai ser mais chatinho porque tem 3 intervalos. Pro primeiro intervalo temos:

a 1 = b 1 - b 0 3 h 1 = 0.06565

c 1 = f x 1 - f x 0 h 1 + h 1 2 b 1 + b 0 3 = 0.22488

d 1 = f x 1 = 0.95802

Para o segundo:

a 2 = b 2 - b 1 3 h 2 = 0.02828

c 2 = f x 2 - f x 1 h 2 + h 2 2 b 2 + b 1 3 = 0.34456

d 2 = f x 2 = 1.09861

E por fim para o terceiro:

a 3 = b 3 - b 2 3 h 3 = - 0.09393

c 3 = f x 3 - f x 2 h 3 + h 3 2 b 3 + b 2 3 = 0.41501

d 3 = f x 3 = 1.29438

Passo 10

Juntando tudo numa função só:

S 3 x = s 1 x = 0.06565 x + 0.5 3 + 0.098476 x + 0.5 2 + 0.22488 x + 0.5 + 0.95802 ,       x ∈ - 1 , - 0.5 s 2 x = 0.02828 x 3 + 0.140897 x 2 + 0.34456 x + 1.09861 ,       x ∈ - 0.5,0 s 3 x = - 0.09393 x - 0.5 3 + 0.41501 x - 0.5 + 1.29438 ,       x ∈ 0,0.5

Resposta

a S 3 x = s 1 x = 1 + 3.43656 x ,   x ∈ 0,0.5

b S 3 x = s 1 x = 1.06641 - 1.0625 x ,   x ∈ - 0.25,0.25

c S 3 x = s 1 x = 4.38125 x - 0.2 3 + 1.3144 x - 0.2 2 - 2.6198 x - 0.2 - 0.5608 ,       x ∈ 0.1,0.2 s 2 x = - 4.38125 x - 0.3 3 - 2.4884 x - 0.3 - 0.814 ,       x ∈ 0.2,0.3

d S 3 x = s 1 x = 0.06565 x + 0.5 3 + 0.098476 x + 0.5 2 + 0.22488 x + 0.5 + 0.95802 ,       x ∈ - 1 , - 0.5 s 2 x = 0.02828 x 3 + 0.140897 x 2 + 0.34456 x + 1.09861 ,       x ∈ - 0.5,0 s 3 x = - 0.09393 x - 0.5 3 + 0.41501 x - 0.5 + 1.29438 ,       x ∈ 0,0.5

Exercício Resolvido #3

Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 161, exercício 6

As tabelas do exercício 4 foram geradas usando as funções abaixo. Use as splines cúbicas construídas no exercício 4 para aproximar f x e f ' x no x dado. Calcule o erro absoluto.

a f x = e 2 x ; aproxime f 0.43 e f ' 0.43 .

b f x = x 4 - x 3 + x 2 - x + 1 ; aproxime f 0 e f ' 0 .

c f x = x 2 cos ⁡ x - 3 x ; aproxime f 0.18 e f ' 0.18 .

d f x = ln ⁡ e x + 2 ; aproxime f 0.25 e f ' 0.25

Passo 1

a Do exercício anterior temos que:

S 3 x = 1 + 3.43656 x ,   x ∈ 0,0.5

Aproximando no ponto desejado temos:

S 3 0.43 = 2.47772

S 3 ' 0.43 = 3.43656

O valor exato da função é:

f 0.43 = e 2 × 0.43 = 2.36316

f ' x = 2 e 2 x

f ' 0.43 = 2 e 2 × 0.43 = 4.72632

Calculando o erro:

E 0.43 = S 3 0.43 - f 0.43 = 0.11456

E ' 0.43 = S 3 ' 0.43 - f ' 0.43 = 1.28976

Deu um erro bastante grande né? Provavelmente porque nós aproximamos e 2 x por uma reta haha. Isso sempre vai acontecer quando tivermos apenas dois pontos, a spline cúbica nos dará uma reta perdendo grande parte da sua acurácia.

Passo 2

b Do exercício anterior temos que:

S 3 x = 1.06641 - 1.0625 x ,   x ∈ - 0.25,0.25

Aproximando no ponto desejado temos:

S 3 0 = 1.06641

S 3 ' 0 = - 1.0625

O valor exato da função é:

f 0 = 1

f ' 0 = - 1

Calculando o erro:

E 0 = S 3 0 - f 0 = 0.06641

E ' 0 = S 3 ' 0 - f ' 0 = 0.0625

Passo 3

c Pegando nosso resultado do exercício anterior novamente:

S 3 x = s 1 x = 4.38125 x - 0.2 3 + 1.3144 x - 0.2 2 - 2.6198 x - 0.2 - 0.5608 ,       x ∈ 0.1,0.2 s 2 x = - 4.38125 x - 0.3 3 - 2.4884 x - 0.3 - 0.814 ,       x ∈ 0.2,0.3

Repare que o ponto desejado aqui é o 0.18 , então usaremos s 1 x :

S 3 0.18 = s 1 0.18 = - 0.507913

s 1 ' x = 13.1437 x - 0.2 2 + 2.6288 x - 0.2 - 2.6198

S 3 ' 0.18 = s 1 ' 0.18 = - 2.66712

O valor exato da função é:

f 0.18 = 0.18 2 cos ⁡ 0.18 - 3 0.18 = - 0.508123

f ' x = 2 x cos ⁡ x - x 2 sin ⁡ x - 3

f ' 0 . 18 = - 2.65162

Calculando o erro:

E 0.18 = S 3 0 . 18 - f 0.18 = 0.00021

E ' 0.18 = S 3 ' 0.18 - f ' 0.18 = 0.0155

Passo 4

d Última gente! Do último exercício temos que:

S 3 x = s 1 x = 0.06565 x + 0.5 3 + 0.098476 x + 0.5 2 + 0.22488 x + 0.5 + 0.95802 ,       x ∈ - 1 , - 0.5 s 2 x = 0.02828 x 3 + 0.140897 x 2 + 0.34456 x + 1.09861 ,       x ∈ - 0.5,0 s 3 x = - 0.09393 x - 0.5 3 + 0.41501 x - 0.5 + 1.29438 ,       x ∈ 0,0.5

Lembra desse monstro? Haha. Como ele quer uma estimativa para a função em x = 0.25 temos que usar s 3 x !

S 3 0.25 = s 3 0.25 = 1.1921

s 3 ' x = - 0.28179 x - 0 . 5 2 + 0.41501

S 3 ' 0.25 = s 3 ' 0.25 = 0.397398

E o valor exato da função é:

f 0.25 = ln ⁡ e 0.25 + 2 = 1.18907

f ' x = e x e x + 2

f ' 0.25 = 0.390991

Calculando o erro (finalmente!):

E 0.25 = S 3 0.25 - f 0.25 = 0.0 0303

E ' 0 . 25 = S 3 ' 0.25 - f ' 0.25 = 0.006407

Resposta

a E 0.43 = 0.11456

E ' 0.43 = 1.28976

b E 0 = S 3 0 - f 0 = 0.06641

E ' 0 = S 3 ' 0 - f ' 0 = 0.0625

c E 0.18 = S 3 0.18 - f 0.18 = 0.00021

E ' 0.18 = S 3 ' 0.18 - f ' 0.18 = 0.0155

d E 0.25 = S 3 0.25 - f 0.25 = 0.00303

E ' 0.25 = S 3 ' 0.25 - f ' 0.25 = 0.006407

Exercícios de Livros Relacionados

A tabela a seguir foi obtida da observação de determinado fenômeno que se sabe é regido pela equação: E = a x + b y Sabendo que: i ) Determine pelo método dos mínimos quadrados aeb . i i ) Qual o erro
Considere a tabela:a) Determinar o polinômio de interpolação, na forma de Lagrange, sobre todos os pontos; b) Calcular f ( 3.5 ) .