Funções Spline
Teoria
Introdução
Até agora, vimos vaaaários métodos de interpolação, pra encontrar a função que mais se aproxima dos conjuntos de pontos que temos. Até aí tudo certo né, analisamos um diagrama de dispersão aqui e ali, e escolhemos o método.
Mas, e se visualmente não encontramos um padrão? Perceba que uma função quadrática é fácil de se achar, uma exponencial, linear e até a hiperbólica também. À medida que temos mais pontos e aumentamos o grau do polinômio interpolador, nossa aproximação e o erro acaba sendo menor quando colocamos mais pontos!
Mas nem sempre ter a maior quantidade de pontos é a função que melhor se adequa a eles. Então, à medida que aumentamos os pontos usados pra interpolar, o nosso polinômio interpolador converge para a função que queremos aproximar?
Eu não julgo se você chutou que sim, já que faz bastante sentido. Só que não é assim que acontece. Quando tempos polinômios de graus muito altos, a função tende a oscilar bastante e quebra tooooooodo o padrão, então é bem difícil chegar numa resposta com um erro pequeno usando apenas um polinômio interpolador e o resultado pode ser uma catástrofe.
Vamos ver um exemplo pra ver se eu convenço vocês? Vamos interpolar a função nos pontos abaixo:
Depois de mandar seu computador calcular esse polinômio de grau pra você, vamos chegar nesse gráfico aqui em baixo onde a linha laranja é a minha função e a azul é o meu polinômio interpolador:
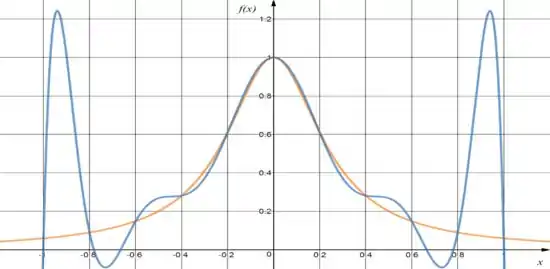
Eai, deu pra entender o que eu quis dizer com oscilar descontroladamente? Repare que para alguns pontos entre e ou entre e o erro é absurdamente alto!
Existem técnicas pra resolver isso sabe, mas vamos estuda-las em ooooooutro momento.
Mas, uma outra solução que é a que vamos usar aqui é separar essa função em vários intervalos e interpolar cada um desses intervalos com polinômios de graus menores que não correm o risco de se descontrolarem haha. E é aí que entram as funções Spline!
Funções Spline
A nossa função deve estar tabelada em pontos , o que vamos fazer é ao invés de encontrar um polinômio de grau n que passe por todos os pontos tabelados, nós iremos interpolar em vários grupinhos de pontos e garantir condições pra que a nossa aproximação seja contínua e tenha derivadas contínuas até a ordem que quisermos.
Cada subintervalo [ , +1], é representado por um polinômio de grau . Vamos chamar de a função spline de grau com nós nos pontos tabelados .
Mas calma, pra não virar baderna, existem algumas regrinhas e imposições.
Se nós temos uma função tabelada nos pontos . Então uma função é chamada de Splines com nós nos pontos dados, maaaaaaas, deve satisfazer as condições de que:
Primeira regra: A cada subintervalo terá grau . Cada par de pontos ela será definida como um polinômio de grau . Repare que usamos maiúsculo para falar da função spline e minúsculo para falar do polinômio que interpola cada par de pontos. O que nós temos é o seguinte:
Segunda regra: deve ser contínua e derivável até a ordem do intervalo dado .
Terceira regra: A função em cada ponto do intervalo, então é chamada de Spline interpolante.
Por enquanto tudo bem? Como não queremos que você se desespere vamos começar devagar com a Spline Linear ok? Se liga!
Spline Linear
A função Spline Linear é definida para cada intervalo dessa forma:
Eu imagino, que a essa altura do campeonato você deve estar cansado de decorar fórmulas, entendo bem o que é isso. Mas dá pra deduzir na hora, porque essa fórmula é uma formula geral pra escrever uma reta que passa por dois pontos.
Vamos ver o exemplo aqui em baixo pra entender direito o que está acontecendo:
Seja a tabela abaixo gerada pela função , encontre a função spline linear que interpola os pontos tabelados:
A primeira coisa que você deve observar é que temos 5 pontos, então nós teremos 4 subintervalos e . Isso significa que vamos usar a mesma fórmula sempre, mas aplicadas nos intervalos [-2,-1]; [-1,0];[0,1] e[1,2].
Usando a fórmula pro primeiro par de pontos temos:
:
E como eu falei podemos simplesmente ignorar essa fórmula e deduzir a reta que passa pelos dois pontos e :
Fazendo :
Substituindo em :
Ou seja,
Sacou?
Aplicando a fórmula para os outros intervalos temos:
:
:
:
Então a função spline linear é a seguinte:
Vamos ficar com algo assim:
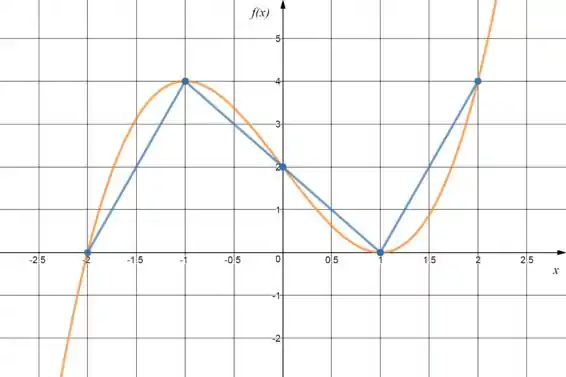
Maneiro né? Mas fala aí, isso te lembra alguma coisa? Se você ainda se lembrar lá do primeiro tópico de interpolação vai perceber que essa foi a maneira mais básica de interpolação que vimos! Antes até de aprendermos a interpolação por sistemas lineares haha.
É claro que como vimos lá esse método tem muita chance de dar ruim né? Mas ele é só o começo das funções spline então vamos dar uma praticada antes de vermos algumas formas mais avançadas!
Algoritmo
Nosso objetivo quando encontramos uma função de interpolação é, em geral, encontrar uma aproximação para um ponto qualquer. E é nisso que vamos focar nosso algoritmo:
Passo 1. Dados iniciais (o que seu programa vai receber de você):
a. Vetor de valores
b. Vetor de valores
c. Valor onde se quer avaliar
Passo 2. Para de a repita o passo 3.
Passo 3. Se , faça o passo 4.
Passo 4. Retorne e FIM.
Pronto, tranquilo né? Não vou falar que é impossível mas daria um belo trabalho criar um algoritmo para encontrar as funções de cada intervalo. Então como nosso propósito normalmente é encontrar uma aproximação em um ponto específico, esse algoritmo é muito mais eficiente.
Funções Spline
Spline Linear
Algoritmo
Exercícios Resolvidos
Exercício Resolvido #1
Lista 4 – Professora Angela – UFRJ – Questão 9 Adaptada
Ajuste com spline linear, os dados abaixo. Estime o valor para .
Passo 1
Primeiro definimos:
Passo 2
Agora é só jogar na fórmula e fim de papo:
:
:
:
Passo 3
Juntando tudo temos:
E uma estimativa para é:
Resposta
Exercício Resolvido #2
Lista 6 – Professora Susana – Questão 1 Adaptada
Em cada função abaixo determine uma aproximação para usando a função spline linear interpolante e calcule o erro cometido.
, , , ,
, , , ,
, , , ,
Passo 1
Primeiro definimos:
Passo 2
Aplicando a fórmula:
:
:
Passo 3
Juntando tudo temos:
E uma estimativa para é:
E o erro é:
Passo 4
Definimos:
Passo 5
Aplicando a fórmula:
:
:
Passo 6
Juntando tudo temos:
E uma estimativa para é:
E o erro é:
Passo 7
Definimos:
Passo 8
Aplicando a fórmula:
:
:
Passo 9
Juntando tudo temos:
E uma estimativa para é:
E o erro é:
Resposta
Exercício Resolvido #3
Elaboração Própria
Seja a tabela abaixo gerada pela função , encontre a função spline linear que interpola os pontos tabelados e esboce o gráfico de ambas as funções.
Passo 1
Primeiro definimos:
Passo 2
Agora é só aplicação de fórmulas:
:
:
:
:
:
Passo 3
Juntando tudo temos:
O gráfico vai ficar assim:
Resposta
Exercício Resolvido #4
Elaboração Própria
Dados , , , , encontre a função spline linear interpolante para . Utilize a função spline calculada para aproximar
e calcule o erro cometido.
Passo 1
Calculando o valor da função nos pontos dados:
Passo 2
Aplicando a fórmula nos intervalos:
:
:
:
Passo 3
Juntando tudo temos:
Passo 4
A integral vai ficar:
Passo 5
O valor exato da integral é:
Então o erro vale: