Equação da Reta Tangente
Produzido por Arthur Melo de AlmeidaTeoria
Fala aí! Bem vindo ao Responde Aí! Bora aprender como encontrar Equação da Reta Tangente?!
Reta Tangente
Antes da gente aprender como encontrar a equação da reta tangente, precisamos saber o que é uma reta tangente! Para isso, eu quero que você imagine uma curva em qualquer formato. Uma reta tangente é uma reta que toca em apenas um ponto dessa curva, assim:
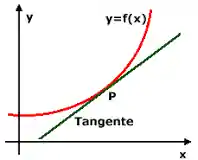
Toda função tem uma infinidade de retas tangentes, cada ponto do domínio tem sua própria reta tangente associado a ele.
Utilizando derivadas podemos calcular a inclinação de uma reta tangente! Usamos isso para fazer estudos sobre pontos máximos e mínimos de uma função, que são aqueles pontos em que a derivada vale
Beleza, agora sabemos o que é uma reta tangente… mas como a gente faz para encontrá-la?
📢 Clique para saber mais:
Como Encontrar a Equação de uma Reta Tangente à Curva
Vamos aprender colocando a mão na massa! Iremos encontrar a equação da reta tangente à função
Passo 1: Substituímos
A nossa reta tangente toca a função
Passo 2: Calculamos
A derivada da função
Pra encontrar a inclinação da reta tangente, calculamos o valor da derivada de
Nesse vídeo abaixo a gente explica o que é a reta tangente e como encontrá-la!
Ou então, você pode terminar de conferir o passo a passo em texto!
Passo 3: Usar a Equação da Reta para Achar a Reta Tangente
No ponto
Sendo
Que organizando para escrevermos da maneira que estamos mais acostumados fica:
Representando essas funções juntas em um gráfico, podemos desenhar:
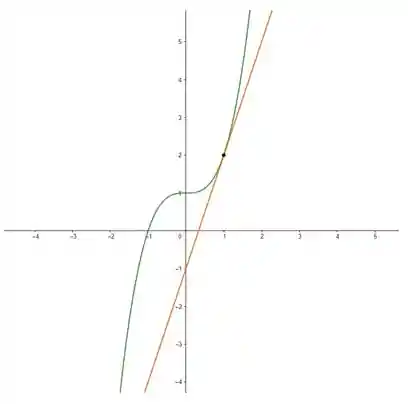
Sendo:
- A função verde:
- A função vermelha:
Exercício: Escreva a equação da reta tangente à curva
Agora vamos praticar com exercícios?!