Exercícios de Reta tangente - Lista de Exercícios Resolvida
Questão 2
Considere a função definida pelo gráfico abaixo,
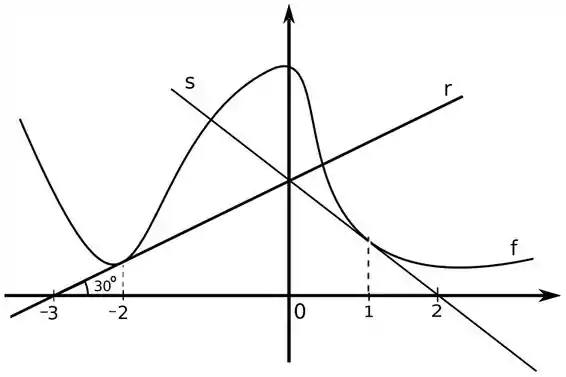
Sabendo que a reta é tangente ao gráfico da em e a reta tangente ao gráfico da em
- Determine a equação da reta
- Determine e
- Determine a equação da reta
- Determine e
Questão 3
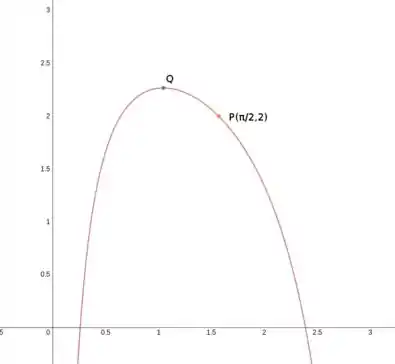
Sendo:
Encontre as equações para:
- A tangente à curva em .
- A tangente horizontal à curva em .
Questão 4
Determine a(s) reta(s) tangente(s) ao gráfico da função a seguir e paralelas a reta abaixo
Ver solução completaQuestão 5
Determine de modo que as retas tangentes ao gráfico de
Sejam no ponto e no ponto .
Ver solução completaQuestão 6
Considere a função .
Usando regras de derivação, determine a derivada de .
Determine a equação da reta tangente ao gráfico de no ponto de abscissa .
Ver solução completaQuestão 7
Considere a função
- Calcule e
- Determine a reta tangente ao gráfico de no ponto
Questão 8
Considere as funções e , ambas definidas no intervalo .
a) Os gráficos das funções f e g possuem ponto de tangência? Se sim, determine as coordenadas do(s) ponto(s) de tangência e a(s) equação(ões) da(s) reta(s) tangente(s) compartilhada(s) pelos dois gráficos nesse(s) ponto(s).
b) Esboce abaixo os gráficos funções f e g (indique ao lado de cada curva a sua respectiva
equação). Caso tenha(m) sido encontrado(s) ponto(s) de tangência no item anterior, esboce
também a(s) reta(s) tangente(s) aos gráficos das funções f e g no(s) ponto(s) de tangencia.
Ver solução completaQuestão 10
Seja uma função tal que a equação da reta tangente ao gráfico de em é
- Seja . Determine a reta tangente ao gráfico da em
- Seja . Determine a reta tangente ao gráfico da em
Questão 11
Seja um número real positivo tal que em um ponto do primeiro quadrante do plano cartesiano as curvas
e
possuem a mesma reta tangente.
O valor de é:
(A) 5
(B) 6
(C) 4
(D) 3
(E) 2
Ver solução completaQuestão 12
Seja derivável, inversível, com inversa derivável e tal que , . A equação da reta tangente ao gráfico da inversa de no ponto é:
Questão 13
2. Considere a equação
- Supondo que é uma função diferenciável de , use derivação implícita para encontrar .
- Determine a equação da reta tangente à curva no ponto .
Questão 14
Determine a equação da reta tangente ao gráfico da função dada passando pelo ponto , caso elas existam.
(c) e
Ver solução completaQuestão 15
Determine a equação da reta tangente ao gráfico da função dada passando pelo ponto , caso elas existam.
(d) e
Ver solução completaQuestão 17
7 - Sabe-se que é uma reta tangente ao gráfico de e paralela à reta . Determine .
Ver solução completaQuestão 18
Questão 3 - Considere a curva plana determinada pela equação . Sabendo que a variável é dada implicitamente em função de próximo do ponto , determine a equação da reta tangente ao gráfico dessa curva no ponto .
Ver solução completaQuestão 19
Seja
Determine a equação da reta tangente ao gráfico de no ponto em que .
Ver solução completaQuestão 21
Determine as equações das retas tangente e normal ao gráfico da função dada em
Ver solução completaQuestão 22
Encontre uma equação para a reta tangente à curva que seja paralela à reta tangente à curva no ponto (1, 2).
Ver solução completaQuestão 23
Encontre uma equação para a reta que contém o ponto (1, 0) e é tangente à curva .
Ver solução completaQuestão 24
Encontre uma equação para a reta que contém o ponto (−2, 3) e é tangente à curva .
Ver solução completaQuestão 25
Prove que não há reta que contenha o ponto (1, 2) e seja tangente à curva
Ver solução completaQuestão 26
a) Encontre a equação da reta tangente ao gráfico de no ponto indicado:
Ver solução completaQuestão 27
. Considere o ponto deslocando-se sobre o gráfico
, para ,
Onde e são medidos em centímetros. Denotemos por o ponto dado pela interseção do eixo com a reta tangente ao gráfico de no ponto . Sabendo que a coordenada do ponto varia a uma taxa constante de , determine com que taxa estará variando a coordenada do ponto no instante em que as coordenadas do ponto forem .
Ver solução completaQuestão 33
Suponha que a equação
defina implicitamente .
Determine a equação da reta tangente ao gráfico de no ponto.
Ver solução completaQuestão 36
Considere a função definida pelo gráfico abaixo, a reta tangente ao gráfico da em e a reta tangente ao gráfico de em .
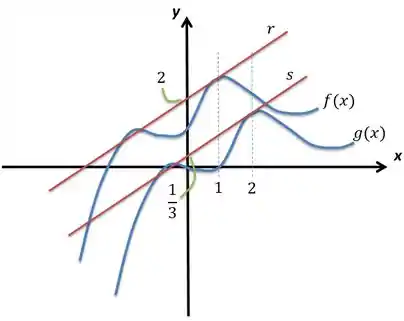
Determine:
A equação das retas e
Ver solução completa
Questão 37
Dentre todas as retas tangentes ao gráfico de , qual é a única que passa pelo ponto ?
Ver solução completaQuestão 38
Q01III) Encontre a equação da reta tangente ao gráfico da função quando .
Ver solução completaQuestão 39
Sejam e funções deriváveis e bijetoras tais que e , para todo Sabe-se que a reta tangente ao gráfico de no ponto de abscissa 3 tem equação . Determine
1. Os valores de
2. a equação da reta tangente ao gráfico de no ponto de abscissa
Ver solução completaQuestão 40
Sabendo que as funções e são deriváveis em seus domínios, determine:
- Equação da reta tangente ao gráfico de pelo ponto
- O valor da constante sabendo que a inclinação da reta tangente ao gráfico de no ponto vale .
Questão 41
- Em cada um dos itens abaixo, determine uma equação para a reta tangente ao gráfico da função no ponto de abscissa .
e.
Ver solução completaQuestão 42
- Em cada um dos itens abaixo, determine uma equação para a reta tangente ao gráfico da função no ponto de abscissa .
i.
Ver solução completaQuestão 43
2. Para os itens e da questão anterior, faça o gráfico da função e da reta obtda. Verifique que, de fato, a reta obtida se comporta como uma reta tangente ao gráfico da função.
m.
Ver solução completaQuestão 44
2. Para os itens e da questão anterior, faça o gráfico da função e da reta obtida. Verifique que, de fato, a reta obtida se comporta como uma reta tangente ao gráfico da função.
h.
Ver solução completaQuestão 45
Determine a equação da reta tangente ao gráfico de cada função a seguir no ponto
a indicado.
no ponto
Ver solução completaQuestão 46
Determine a equação da reta tangente ao gráfico de cada função a seguir no ponto
a indicado.
no ponto
Ver solução completaQuestão 47
Determine a equação da reta tangente ao gráfico de cada função a seguir no ponto
a indicado.
no ponto
Ver solução completaQuestão 48
Determine a equação da reta tangente ao gráfico de cada função a seguir no ponto
a indicado.
no ponto
Ver solução completaQuestão 49
- Em cada um dos itens abaixo, determine uma equação para a reta tangente ao gráfico da função no ponto de abscissa .
n.
Ver solução completaQuestão 50
Seja . Determine a equação da reta tangente ao gráfico de no ponto de abscissa .
Ver solução completaQuestão 51
Ache os pontos sobre a curva para os quais a reta tangente é horizontal
Ver solução completaQuestão 52
Considere a função definida por:
- Encontre o valor de para que a função seja contínua.
- Encontre a reta tangente a no ponto .
Questão 53
6. Sabendo que a reta é tangente ao gráfico da função diferenciável em , determine e .
Ver solução completaQuestão 55
Determinar a reta tangente, o hiperplano normal e a curvatura da curva
Em no ponto .
Ver solução completaQuestão 56
Considere a função . Seja a equação da reta tangente ao gráfico de no ponto onde . Logo é igual a:
Questão 57
Sejam um número real e a curva determinada pela equação . O ponto está sobre a reta tangente ao gráfico da curva no ponto . O valor de é:
Escolha uma:
(A) 489
(B) 477
(C) 475
(D) 482
(E) 479
Ver solução completaQuestão 58
Sabe-se que o ponto está sobre a curva
de tal forma que a reta tangente à curva no ponto determina junto com os eixos coordenados um triângulo de área . O valor de é
Escolha uma:
(A) 94
(B) 102
(C) 106
(D) 108
(E) 110
Ver solução completaQuestão 60
Seja uma constante e seja . Encontre o valor de para que a inclinação da reta tangente ao gráfico de no ponto seja 5.
Ver solução completaQuestão 61
Questão 1:
b) Considere a função dada por
Sabendo que é a reta tangente ao gráfico de no ponto , determine o valor das constantes reais e .
Ver solução completaQuestão 62
3) A reta tangente ao gráfico da função no ponto onde passa no ponto:
Questão 63
Questão 5:
Determine a equação da reta tangente ao gráfico da função que passa pelo ponto .
Ver solução completaQuestão 65
Suponha que é dada implicitamente pela equação . Suponha que .
Determine a equação da reta tangente ao gráfico de no ponto de abscissa .
Ver solução completaQuestão 67
Prove que não há reta que contenha o ponto (1, 5) e seja tangente à curva
Ver solução completaQuestão 68
ME03) Seja uma função qualquer, e considere as afirmações abaixo:
- A reta tangente a em um dado ponto pode interceptar seu gráfico em outro ponto
- possui reta tangente em todo ponto de seu gráfico
Escolha a alternativa correta:
- Ambas são falsas
- Ambas são verdadeiras
- é falsa e é verdadeira
- é verdadeira e é falsa
Questão 69
Q03) Sejam . Decida se cada proposição abaixo é verdadeira ou falsa:
- Se é a equação da reta tangente ao gráfico da função , então
Questão 70
Q03) Sejam . Decida se cada proposição abaixo é verdadeira ou falsa:
- Se é a equação da reta tangente ao gráfico da função , então
Questão 73
Dada a função , determine a equação da reta tangente no ponto , marcando a única alternativa correta.
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 74
Determine as equações das duas retas que passam pelo ponto e que são tangentes a curva
Ver solução completaQuestão 75
Obtenha dois pontos P e Q pertencentes ao gráfico de g(x) = 2x³ − 3x² − 3x para os quais as respectivas retas tangentes são paralelas à reta com equação .
Ver solução completaQuestão 76
5) Seja com . Pelo ponto passam duas retas que tangenciam o gráfico de nos pontos e .
O valor de é
Escolha uma:
A.
B.
C.
D.
E.
Ver solução completaQuestão 77
11] Encontre a declividade da reta tangente à curva de interseção da superfície com o plano no ponto . Trace um esboço. Interprete essa declividade como uma derivada parcial
Ver solução completaQuestão 78
Sabe-se que a reta é tangente à curva determinada pela equação no ponto O valor de é
Ver solução completa
Questão 82
C2) Determine uma equação para a reta que passa por e tem coeficiente angular igual a .
Ver solução completaQuestão 84
Determine a equação do plano tangente ao gráfico de no ponto indicado.
b) no ponto .
Ver solução completaQuestão 85
Determine a equação do plano tangente ao gráfico de no ponto indicado.
a) , no ponto .
Ver solução completaQuestão 87
6. Seja a função definida por
- Calcule .
- Determine a equação da reta tangente ao gráfico de no ponto .
- Mostre que nenhuma reta tangente ao gráfico de passa pela origem.
Questão 88
Considere a função , que está definida para
- Calcule
- Encontre a equação da reta que é tangente ao gráfico de no ponto
Questão 89
3. Considere a função , onde .
- Sabendo que , encontre os valores de e .
- Sabendo que a reta tangente ao gráfico de no ponto para pelo ponto , encontre o valor de .
Questão 92
Questão 3: Seja dada por
c) Encontre o ponto do gráfico de onde a reta tangente é paralela à reta .
Ver solução completaQuestão 93
Questão 4. Seja a superfície dada pela parte da esfera , calota esférica, que está acima do plano . Considere a função definida em uma região de que contém .
(b) Calcule dois vetores tangentes e um vetor normal a em um ponto genérico;
Ver solução completaQuestão 94
4 Considere a função
a) Determine a equação cartesiana da reta tangente ao gráfico de no ponto de abscissa .
b) Obtenha três pontos e pertencentes ao gráfico de , para os quais as retas tangentes são paralelas à reta
Ver solução completaQuestão 95
3 – Determine a equação da reta tangente à seguinte curva espacial em :
Ver solução completaQuestão 97
1.3. Encontre uma parametrização para a curva de nível de nos casos:
a. ,
Determine a reta tangente às curvas acima nos pontos , e , respectivamente.
Ver solução completaQuestão 98
1.3. Encontre uma parametrização para a curva de nível de nos casos:
a. ,
Determine a reta tangente às curvas acima nos pontos , e , respectivamente.
Ver solução completaQuestão 99
Considere a curva
- Mostre que o traço está contida no plano
- Calcule .
- Determine a equação da reta tangente à trajetória de no ponto
Questão 100
Determine a equação da reta tangente às seguintes curvas, nos pontos indicados. Esboce o gráfico em cada caso:
(c)
Ver solução completaQuestão 101
Determine a equação da reta tangente às seguintes curvas, nos pontos indicados. Esboce o gráfico em cada caso:
(b)
Ver solução completaQuestão 102
4) Determine as equações das retas tangente e normal ao gráfico da curva no ponto
Ver solução completaQuestão 103
As parábolas possuem duas retas tangentes comuns.
Determine as equações dessas retas tangentes.
Ver solução completaQuestão 104
Use a derivação implícita para encontrar uma equação da reta tangente à curva , no ponto .
Ver solução completaQuestão 105
5) Seja número real tal que no ponto de interseção dos gráficos e as respectivas retas tangentes sejam perpendiculares.
O valor de é
Escolha uma:
A.
B.
C.
D.
E.
Ver solução completaQuestão 107
Considere a função .
- Obtenha a equação da reta tangente ao gráfico de no ponto de abscissa .
- Existe uma outra reta tangente ao gráfico de e que é paralela à reta do item anterior. Determine o ponto de tangência desta reta com o gráfico de ..
Questão 108
Considere na equação e determine:
(a)
(b) a derivada
(c) a equação da reta tangente ao gráfico de no ponto
Ver solução completaQuestão 109
3 – Determine a equação da reta tangente à seguinte curva espacial em :
Ver solução completaQuestão 114
Se uma bola for atirada ao ar com velocidade de 10 m/s sua altura, em metros, será descrita por . Determine a velocidade da bola quando
Ver solução completaQuestão 115
Supondo que a equação da reta tangente à curva no ponto (4,3) passa no ponto (0,2) determine e .
Ver solução completaQuestão 117
Encontre uma equação para a reta tangente à curva que seja paralela à reta .
Ver solução completaQuestão 118
- Em cada um dos itens abaixo, determine uma equação para a reta tangente ao gráfico da função no ponto de abscissa .
b.
Ver solução completaQuestão 119
- Em cada um dos itens abaixo, determine uma equação para a reta tangente ao gráfico da função no ponto de abscissa .
d.
Ver solução completaQuestão 120
- Em cada um dos itens abaixo, determine uma equação para a reta tangente ao gráfico da função no ponto de abscissa .
g.
Ver solução completaQuestão 121
Encontre a equação da reta tangente ao gráfico da função no ponto .
Ver solução completaQuestão 122
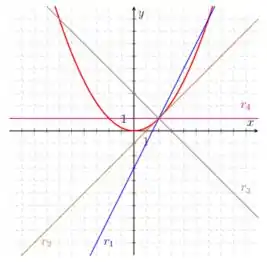
C6) Na figura abaixo, há o gráfico da função e de quatro retas que passam pelo par ordenado . Qual dessas retas você escolheria para chamar de reta tangente ao gráfico de no ponto ?
Questão 123
Encontre as equações das retas tangentes às curvas dadas nos pontos dados. Esboce o gráfico e a reta tangente.
Ver solução completaQuestão 124
Encontre as equações das retas tangentes às curvas dadas nos pontos dados. Esboce o gráfico e a reta tangente.
Ver solução completaQuestão 125
Encontre as equações das retas tangentes às curvas dadas nos pontos dados. Esboce o gráfico e a reta tangente.
e
Ver solução completaQuestão 126
Um avião de caça dá um vôo rasante, percorrendo a trajetória determinada pelo gráfico da função e efetua seus disparos segundo a direção de uma reta tangente como mostra a figura
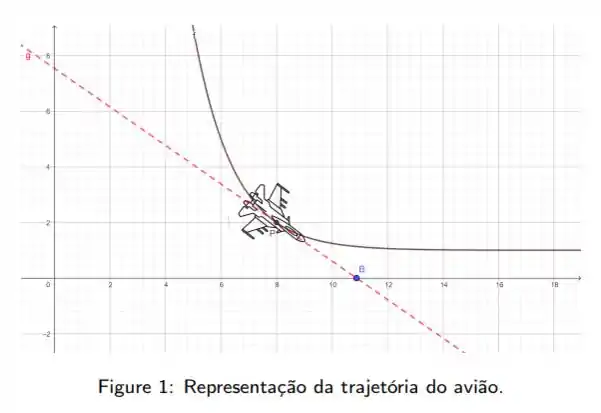
Determine a equação da reta tangente ao gráfico de em um ponto genérico .
Ver solução completaQuestão 127
Um avião de caça dá um vôo rasante, percorrendo a trajetória determinada pelo gráfico da função e efetua seus disparos segundo a direção de uma reta tangente como mostra a figura
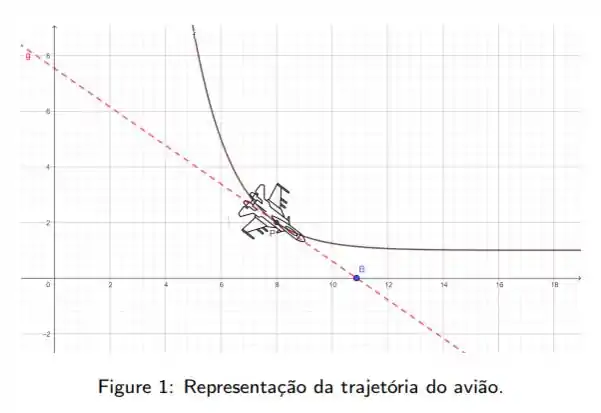
Se o avião dispara a partir do ponto , em que coordenada atingirá o eixo das abscissas?
Ver solução completaQuestão 129
2. Para os itens e da questão anterior, faça o gráfico da função e da reta obtda. Verifique que, de fato, a reta obtida se comporta como uma reta tangente ao gráfico da função.
Questão 130
Sejam e r a reta tangente ao gráfico de no ponto de abcissa . Um ponto que pertence a essa reta é:
Questão 131
A reta normal ao gráfico de uma função em um ponto é definida como a reta que passa por e é perpendicular à reta tangente ao gráfico da função em . Ache uma equação da reta normal ao gráfico de no ponto de abscissa .
Ver solução completaQuestão 132
Usando as ideias dos exercícios , e ., explique de maneira informal por que o coeficiente angular da reta tangente ao gráfico de uma função no ponto de abscissa é
Ver solução completaQuestão 136
Existe algum ponto do gráfico de onde a reta tangente é paralela à reta ?
Ver solução completaQuestão 138
Os gráficos de e admitem retas tangentes paralelas (possivelmente em pontos distintos)? Dê exemplos
Ver solução completaQuestão 139
Existe algum ponto do gráfico de que tem reta tangente paralela à reta ?
Ver solução completaQuestão 141
Sejam um intervalo aberto e uma função. Dado , a reta tangente ao gráfico de no ponto é a (única) reta que passa pelo ponto e tem inclinação igual a
,
Ver solução completaQuestão 142
Dada a curva , ache sobre esta curva um ponto cuja reta tangente passa pelo ponto
Questão 143
Determine a equação da reta tangente ao gráfico da função dada passando pelo ponto , caso elas existam.
(e) e
Ver solução completaQuestão 146
Quantas retas tangentes à curva passam pelo ponto ? Determine as equações dessas retas tangentes.
Ver solução completaQuestão 147
Ache o ponto em que a reta tangente ao gráfico de corta o eixo no ponto
Ver solução completaQuestão 151
- Em cada um dos itens abaixo, determine uma equação para a reta tangente ao gráfico da função no ponto de abscissa .
m.
Ver solução completaQuestão 152
- Em cada um dos itens abaixo, determine uma equação para a reta tangente ao gráfico da função no ponto de abscissa .
h.
Ver solução completaQuestão 153
- Em cada um dos itens abaixo, determine uma equação para a reta tangente ao gráfico da função no ponto de abscissa .
f.
Ver solução completaQuestão 154
- Em cada um dos itens abaixo, determine uma equação para a reta tangente ao gráfico da função no ponto de abscissa .
j.
Ver solução completaQuestão 155
- Em cada um dos itens abaixo, determine uma equação para a reta tangente ao gráfico da função no ponto de abscissa .
k.
Ver solução completaQuestão 156
Parte 1: Determine a equação da reta tangente ao gráfico de no ponto de abscissa
Parte 2: Esboce o gráfico de e da reta tangente
Ver solução completaQuestão 157
3. Extras
b) Considere a função definida por
Determine a reta tangente ao gráfico de no ponto de abscissa
Ver solução completaQuestão 158
Seja . Determine o ponto do gráfico de em que a reta tangente, nesse ponto seja paralela ao eixo .
Ver solução completaQuestão 159
Se denota a posição de uma partícula em movimento no instante sobre uma reta, determine os instantes em que a velocidade é de .
Ver solução completaQuestão 160
- Em cada um dos itens abaixo, determine uma equação para a reta tangente ao gráfico da função no ponto de abscissa .
Ver solução completaQuestão 161
2. Para os itens e da questão anterior, faça o gráfico da função e da reta obtda. Verifique que, de fato, a reta obtida se comporta como uma reta tangente ao gráfico da função.
j.
Ver solução completaQuestão 162
6. Seja para .
(b) Encontre a equação da reta tangente ao gráfico de no ponto .
Ver solução completaQuestão 163
Determine os pontos do gráfico de em que a tangente seja paralela à reta .
Ver solução completaQuestão 164
Quantas retas tangentes ao gráfico são paralelas à reta Determine as equações dessas retas tangentes.
Ver solução completaQuestão 165
Seja . Determine o que se pede, justificando adequadamente o que não há.
A função é inversível?
Determine uma expressão para a inversa de .
Determine a equação da reta tangente ao gráfico , a função inversa de , em .
Ver solução completaQuestão 167
Considere a curva dada pela equação
(b) Encontre a equação da reta tangente à curva dada no ponto .
Ver solução completaQuestão 168
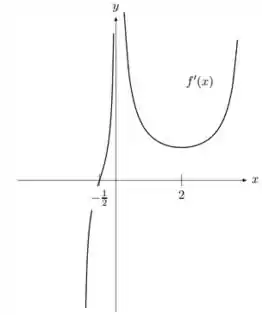
Seja uma função derivável definida no intervalo . O gráfico abaixo é o gráfico da derivada de , ou seja, o gráfico de :
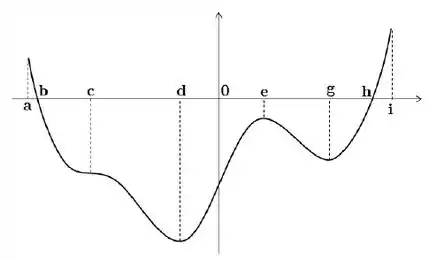
Decida se cada uma das afirmações abaixo é verdadeira ou falsa, justificando sua resposta
- A reta tangente ao gráfico de em tem inclinação negativa
Questão 169
Dados os paraboloides e
- Escreva a integral do volume correspondente.
Questão 171
Considere a função
a) Calcule
b) Encontre a equação da reta tangente ao gráfico de no ponto
Ver solução completaQuestão 172
Considere a função racional .
a) Calcule
b) Encontre a equação da reta tangente ao gráfico de no ponto
Ver solução completaQuestão 176
C7) Entre as retas dos exercícios C4 e C5, qual é a mais parecida com a reta tangente escolhida no
exercício C6? O que mudou entre os exercícios C4 e C5 para que uma dessas retas fosse mais
parecida com a reta tangente? Como você faria para encontrar uma outra reta ainda mais parecida
com a reta tangente?
Ver solução completaQuestão 177
Parte 1: Determine a equação da reta tangente ao gráfico de no ponto de abscissa
Parte 2: Esboce o gráfico de e da reta tangente
Ver solução completaQuestão 178
Obtenha dois pontos P e Q pertencentes ao gráfico de g(x) = 2x³ − 3x² -3x para os quais as respectivas retas tangentes são paralelas à reta com equação y = 3x − 2.
Ver solução completaQuestão 179
Resolva as seguintes questões:
- Dada , calcule a equação da reta tangente ao gráfico de no ponto
Questão 180
2. O ponto está sobre a curva .
a) se é o ponto , use sua calculadora para determinar a inclinação da reta secante , com precisão de seis casas decimais, para os seguintes valores:
a) 1,5
b) 1,9
c) 1,99
d) 1,999
e) 2,5
f) 2,1
g) 2,01
h) 2,001
Ver solução completaQuestão 181
2. O ponto está sobre a curva .
c) Usando a inclinação da parte (b), encontre uma equação da reta tangente à curva em .
Ver solução completaQuestão 182
2. O ponto está sobre a curva .
b) Usando os resultados da parte (a), estime o valor da inclinação da reta tangente à curva no ponto .
Ver solução completaQuestão 183
3. Determine o coeficiente angular da curva no ponto dado e uma equação da reta tangente em .
b)
Ver solução completaQuestão 184
1. Um tanque com capacidade para 1000 litros de água é drenado pela base em meia hora. Os valores na tabela mostram o volume de água remanescente no tanque (em litros) após minutos.
a) Se é o ponto sobre o gráfico de , encontre as inclinações das retas secantes , onde é o ponto sobre o gráfico com e .
Ver solução completaQuestão 185
1. Um tanque com capacidade para 1000 litros de água é drenado pela base em meia hora. Os valores na tabela mostram o volume de água remanescente no tanque (em litros) após minutos.
b) Estime a inclinação da reta tangente em pela média das inclinações de duas retas secantes.
Ver solução completaQuestão 186
Sejam , em que , e . Determine e sabendo que e possuem a mesma reta tangente no ponto de abscissa e que o ponto pertence à reta tangente ao gráfico de no ponto de abscissa .
Ver solução completaQuestão 187
3. Determine o coeficiente angular da curva no ponto dado e uma equação da reta tangente em .
a) ,
Ver solução completaQuestão 188
3. Determine o coeficiente angular da curva no ponto dado e uma equação da reta tangente em .
d)
Ver solução completaQuestão 189
3.33. Seja uma função dada implicitamente pela equação . Admitindo que é derivável, determine a reta tangente ao gráfico de no ponto .
Ver solução completaQuestão 190
3.34. Seja derivável, onde é um intervalo aberto contendo . Suponha que , para todo ∈ . Encontre e a equação da reta tangente ao gráfico de no ponto .
Ver solução completaQuestão 191
3. Determine o coeficiente angular da curva no ponto dado e uma equação da reta tangente em .
e)
Ver solução completaQuestão 192
3. Determine o coeficiente angular da curva no ponto dado e uma equação da reta tangente em .
f)
Ver solução completaQuestão 193
Considere a reta tangente ao gráfico de em . Se está nessa reta, então:
Questão 194
- Em cada um dos itens abaixo, determine uma equação para a reta tangente ao gráfico da função no ponto de abscissa .
c.
Ver solução completaQuestão 195
Considerem o arco de círculo dado pelo gráfico da função com . Seja a reta tangente à no ponto ). Seja o triângulo determinado pela origem e os pontos (caso existam) em que corta os eixos coordenadas. Determine, se possível, os valores de para os quais a área de seja mínima.
Ver solução completaQuestão 196
Seja a função f(x) = 3x + 2:
a) Determine a equação da reta tangente ao gráfico dessa função no ponto x = −1.
Ver solução completaQuestão 197
Para cada curva abaixo, determine uma equação da reta tangente no ponto requerido.
Ver solução completaQuestão 198
Determine a equação da reta tangente ao gráfico das seguintes funções, no ponto de abscissa
dada:
Ver solução completa
Questão 199
Encontre a reta tangente à astroide + , em que a > 0 é um constante, em um
ponto da curva.
Ver solução completaQuestão 200
Encontre os pontos sobre a elipse onde a reta tangente tem inclinação 1. Para esses pontos determine, também, a equação da reta normal à curva.
Ver solução completaQuestão 202
Seja . Considere a função tal que
Sabendo que é um ponto de inflexão do gráfico de , faça o que se pede:
a) Determine e o valor da constante .
b) Determine .
c) Determine a equação da reta tangente ao gráfico de em
Ver solução completaQuestão 204
- Em cada um dos itens abaixo, determine uma equação para a reta tangente ao gráfico da função no ponto de abscissa .
l.
Ver solução completaQuestão 205
2. Para os itens e da questão anterior, faça o gráfico da função e da reta obtda. Verifique que, de fato, a reta obtida se comporta como uma reta tangente ao gráfico da função.
k.
Ver solução completaQuestão 206
2. Determine o que se pede.
f. Use o item anterior para encontrar uma equação para a reta que é tangente ao gráfico da função no ponto da abscissa .
Ver solução completaQuestão 207
Determine uma equação para a reta que é tangente ao gráfico de e paralela à reta .
Ver solução completaQuestão 208
Encontre uma parábola que passa pelo ponto e cujas retas tangentes em e tenham inclinações e respectivamente.
Ver solução completaQuestão 209
Encontre uma parábola que passa pelo ponto e cujas retas tangentes em e tenham inclinações e respectivamente.
Ver solução completaQuestão 210
Seja:
Calcule a derivada de .
Determine a equação da reta tangente ao gráfico de em .
Ver solução completaQuestão 211
Questão 1:
a) Considere a função dada por
Determine a equação da reta tangente ao gráfico de em .
Ver solução completaQuestão 212
Considere a função
Definida para
- Aplicando a definição de derivada de uma função, calcule .
- Determine a equação da reta tangente ao gráfico de no ponto de abscissa .
Questão 214
Determine a equação da reta tangente ao gráfico das seguintes funções, no ponto de abscissa
dada:
Ver solução completa
Questão 215
Determine a equação da reta tangente ao gráfico das seguintes funções, no ponto de abscissa
dada:
Ver solução completaQuestão 216
Determinar a equação da reta tangente à curva , que seja paralela à reta . Esboçar os gráficos da função, da reta dada e da reta tangente encontrada. Determine, também, a reta normal à essa curva passando pelo ponto de tangência.
Ver solução completaQuestão 218
Seja a função dada por . Para quantos valores de o gráfico de tem reta tangente horizontal?
- Nenhum
- 1
- 2
- 3
- Infinitos
Questão 219
Considere para .
(b) Encontre a equação da reta tangente ao gráfico de no ponto .
Ver solução completaQuestão 220
Mostre que para é invertível e calcule . Encontre a equação da reta tangente ao gráfico de no ponto .
Ver solução completaQuestão 221
Determine a equação da reta tangente ao gráfico da função dada passando pelo ponto , caso elas existam.
(b) e
Ver solução completaQuestão 225
Seja uma função definida em , contínua em todo o seu domínio e satisfazendo as condições abaixo:
e
Suponha que o gráfico de é dado pela figura abaixo:
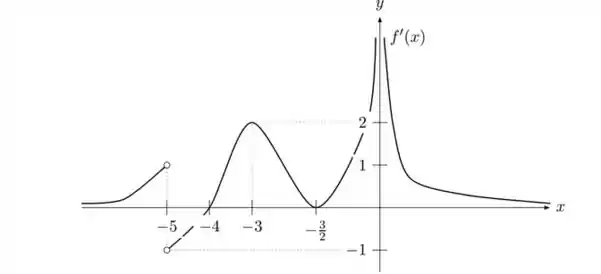
Responda, justificando, o que se pede:
Os pontos onde a reta tangente ao gráfico de é horizontal;
Ver solução completaQuestão 226
Determine as equações das retas tangente e normal ao gráfico da função dada em
Ver solução completaQuestão 227
Seja uma função contínua em tal que:
Suponha que o gráfico de seja dada pela figura abaixo:
Responde o que se pede:
Os pontos onde a reta tangente ao gráfico de é horizontal;
Ver solução completaQuestão 229
1. Um tanque com capacidade para 1000 litros de água é drenado pela base em meia hora. Os valores na tabela mostram o volume de água remanescente no tanque (em litros) após minutos.
c) Use um gráfico da função para estimar a inclinação da tangente em . (Essa inclinação representa a razão na qual a água flui do tanque após 15 minutos.)
Ver solução completaQuestão 230
3. Na figura a seguir, estão representadas uma função e a reta tangente ao gráfico dessa função no ponto .
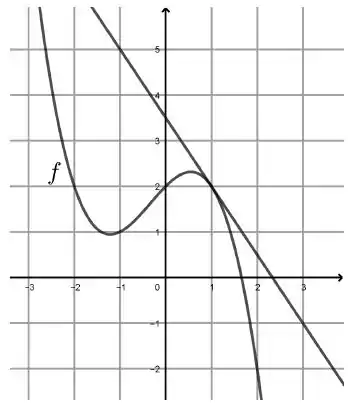
O valor da derivada é:
a)
b)
c)
d)
e)
Ver solução completaQuestão 231
11.2
b) Obtenha a equação da reta tangente à curva dada por no ponto .
Ver solução completaQuestão 232
2.5. Ache a reta tangente à interseção do gráfico da função com o cilindro no ponto .
Ver solução completaQuestão 234
2.7. Determine a equação da esfera que tangencia a superfície nos pontos e .
Ver solução completaQuestão 236
Dentre todas as retas tangentes ao gráfico de , a única que passa pelo ponto é:
- ;
- ;
- ;
- ;
Questão 237
Mostre que qualquer par de retas tangentes à parábola , () tem como interseção um ponto que está numa reta vertical que passa pelo ponto médio do segmento que une os pontos de tangência destas retas.
Ver solução completaQuestão 238
Determine todos os pontos sobre a curva tais que a reta tangente à curva em seja paralela à reta .
Ver solução completaQuestão 239
Considere a parametrização dada por . Determine a equação da reta tangente à trajetória de no ponto . Esboce a curva e reta na mesma figura.
Ver solução completaQuestão 240
Determine todos os números positivos tais que a curva corta a reta .
Ver solução completaQuestão 241
Mostre que as retas tangentes às curvas e no ponto são perpendiculares.
Ver solução completaQuestão 242
Seja uma função definida pela equação
(a) Encontre uma equação da reta tangente ao gráfico da curva no ponto .
Ver solução completaQuestão 243
Encontre uma equação da reta tangente ao gráfico da curva no ponto .
Ver solução completaQuestão 244
Determine os valores das constantes e para que o gráfico da função e a curva definida implicitamente por tenham a mesma reta tangente no ponto .
Ver solução completaQuestão 245
Uma função é definida implicitamente por e pela condição . Calcule .
Ver solução completaQuestão 246
Seja uma função definida pela equação
(b) Existem pontos dessa curva onde a reta tangente é vertical? Justifique.
Ver solução completaQuestão 247
Prove que as retas tangentes a uma elipse ou uma hipérbole interceptam esses conjunto apenas uma vez.
Ver solução completaQuestão 248
Para cada curva abaixo, determine uma equação da reta tangente no ponto requerido.
Ver solução completaQuestão 249
Seja a função f(x) = 3x + 2:
b) Explique de que forma a resposta do item (a) poderia ter sido obtida exclusivamente a partir de considerações geométricas, sem realizar nenhum cálculo.
Ver solução completaQuestão 250
Considere todas as retas que são simultaneamente tangentes às parábolas e . Então o produto dos coeficientes angulares dessas retas é:
Questão 251
7.27. (Transferência Fuvest 2012) Seja . Então, o coeficiente angular máximo das retas tangentes ao gráfico de é
a. ;
b. ;
c. ;
d. ;
e. .
Ver solução completaQuestão 252
Seja derivável em e seja dada por , . Suponha que é ponto crítico
de . Prove que
Prove que a reta tangente ao gráfico de f no ponto de
abscissa passa pela origem.
Ver solução completaQuestão 254
1.7. Seja .
c. Determine o vetor tangente à curva , que você encontrou no item anterior, no ponto .
Ver solução completaQuestão 256
Existe algum ponto do gráfico de cuja reta tangente é paralela à reta ?
Ver solução completaQuestão 257
As curvas e têm a mesma reta tangente no ponto . Quais são os valores de e ?
Ver solução completaQuestão 258
Determine a equação da reta tangente ao gráfico da função , no ponto da abscissa 1.
Ver solução completaQuestão 263
Encontre uma equação para a reta tangente à curva que seja paralela à reta .
Ver solução completaQuestão 267
Sabendo que é tangente ao gráfico da em , determine:
- e
- A equação da reta tangente ao gráfico de em
Questão 268
Considere a função
Determine o domínio de
Calcule a derivada de
Determine uma expressão para a inversa de
Determine a equação da reta tangente ao gráfico da inversa de em
Ver solução completaQuestão 269
Considere a função dada por
Determine a derivada de e depois calcule o valor de .
Encontre a reta tangente ao gráfico de no ponto .
Ver solução completaQuestão 270
(a) Determine a equação da reta tangente ao gráfico no ponto
(b) Encontre a área da região do plano delimitada pela reta do item anterior, o gráfico de e o eixo
Ver solução completaQuestão 271
b) Encontre a equação da reta tangente ao gráfico de no ponto indicado:
Ver solução completaQuestão 272
Encontre uma parábola que passa pelo ponto e cujas retas tangentes em e tenham inclinações e respectivamente.
Ver solução completaQuestão 273
3. Determine o coeficiente angular da curva no ponto dado e uma equação da reta tangente em .
c)
Ver solução completaQuestão 274
C3) Qual é o coeficiente angular da reta que passa pelos pontos e (assuma que ).
Ver solução completa

