Área com Integral imprópria
Produzido por Arthur Melo de AlmeidaTeoria
Funções que não tem fim
Já vimos como calcular vários tipos de área entre curvas e eixos, mas e se eu te pedir pra calcular essa área hachurada aqui?
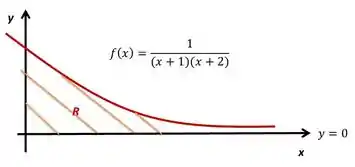
O que a gente faria, dado que é usar a nossa formulinha
Pela figura, temos que .
O problema é que a função nunca toca o eixo , ele é uma assíntota horizontal! E AGORA, COMO VOU ACHAR O OUTRO LIMITE DE INTEGRAÇÃO??
Calma, jovem, é simples! Como o título já deu spoiler lá em cima, nesses casos vamos calcular a área fazendo uma integral imprópria:
Tudo joia na jiboia?
Funções que explodem
Um outro caso que pode aparecer é pedir para calcular a área entre o eixo e
Repare que o denominador se anula em , o que faz a função explodir pro infinito!!

Ok, me empolguei um pouco. Vamos ver isso aí com mais matemática e menos fogo:
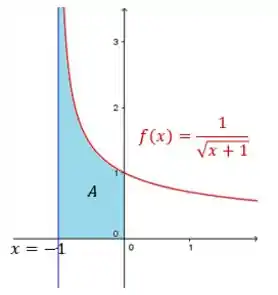
Quando nos deparamos com uma assíntota vertical como essa, vamos fazer:
Portanto, #ficaadica: antes de simplesmente escrever a fórmula da área e sair calculando, dá uma olhada e vê se não tem ponto que zera o denominador! Se for o caso a integral vai ser imprópria :)
Funções que explodem
Exercícios Resolvidos
Exercício Resolvido #1
UNICAMP - Cálculo 1 - P3 2008.1 a – 4
Calcule a área da região limitada pelo eixo e pelo gráfico de , para
Passo 1
É o seguinte, eu não vou nem esboçar esse gráfico por que eu não faço ideia dos detalhes dele.
Juro, não faço ideia de como fica um polinômio do primeiro grau multiplicado a uma exponencial.
Agora, Eu sei que se ele for um gráfico positivo no intervalo pedido , então sua área será dada por:
Caso seja negativo, será o oposto:
Agora, independente de como seja o gráfico, sei que ele só tem uma raiz, justamente em pois o polinômio ali zeraria. Como exponencial é sempre positiva e o é positivo no intervalo podemos dizer que a área será dada pela primeira integral que coloquei. Agora, ele não tem limite superior, né? Bom, isso significa que teremos de usar uma integral imprópria. Vai ser
Temos que fazer o limite,
Passo 2
Agora, para facilitar a análise eu vou primeiro integrar e depois usar os limites, ok?
Integral por partes, né? Pelo LIATE nosso será :
Passo 3
Agora podemos aplicar os limites de integração, lembrando que se trata de uma integral imprópria:
Para esse limite podemos usar L’Hospital:
Assim, temos a resposta:
Resposta
Exercício Resolvido #2
UFRJ - Cálculo 1 - P2 2015.1 - 3a
Considere a região dada por
Determine, se possível, a área de .
Discuta a convergência da integral
Passo 1
Para resolver a maioria das questões nós começamos esboçando o gráfico dado para então calcular a área gerada por ele. Acontece que nessa questão isso não é necessário, uma vez que basta sabermos algumas características da região para já saber como ficará a nossa integral.
Vamos pensar: trabalhamos numa região onde e que fica entre e . Acontece que essa curva, o será sempre positivo, já que é produto de duas funções positivas para qualquer . Com isso, a gente sabe que a área será a integração dessa curva de até o limite máximo que assume. Ué, mas não está limitado na região. Bom, isso só pode significar uma coisa: o limite de integração superior é .
Assim, a conclusão é essa função aqui:
Vamos fazer esse cara pela integração por partes.
Passo 2
Vamos chamar pelo LIATE o termo algébrico (polinômio) de e o resto de .
Vamos resolver essa outra integral para depois voltar para cá.
Passo 3
Caímos em outra integral com polinômio e exponencial, novamente vamos usar integração por partes e novamente usamos o LIATE com o sendo o novo
Vamos voltar à expressão inicial e substituir essa integral:
Passo 4
Para substituir os limites a gente precisa tomar cuidado, já que essa é uma integral imprópria:
Esse termo do limite que sobrou gera indeterminação do tipo , então podemos usar L’Hospital até que essa indeterminação não seja mais gerada:
Portanto,
Passo 5
Olha para essa integral que foi pedida:
O cara pergunta se essa integral aí vai convergir. Bom, a função que ele está integrando é basicamente a mesma da qual calculamos a área, com o detalhe desse . Como a gente viu, para esses mesmo limites de integração, a integral convergiu antes. Ora, como por definição será sempre menor ou igual a , a gente conclui que:
Com isso, pelo teorema da comparação, vemos que a integral do item também vai convergir!
Resposta
Exercício Resolvido #3
UFRJ - Cálculo 1 - P2 2013.2 - 4
Considere as funções:
E seja a região ilimitada definida por .
- Faça um esboço de
- Calcule a área de
Passo 1
Para o temos que as duas funções vão encontrar em:
Já para elas não encontram, pois .
Como todas essas funções são conhecidas, esboçamos:
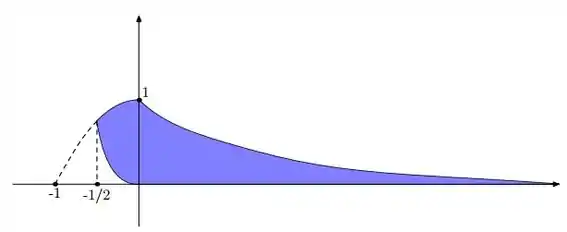
Passo 2
Temos que separar a integral em duas regiões:
Resolvendo, podemos integrar termo à termo:
Substituindo os valores:
Passo 3
Já a outra:
Segue que área é a soma desses dois resultados:
Resposta
Exercício Resolvido #4
UNICAMP - Cálculo 1 - Exame 2012 Diurno - 2
Determine a área abaixo da função
No intervalo
Passo 1
Para essa não é necessário nem fazer o esboço. Como raiz quadrada sempre gera um número positivo, então a área formada será a simples integral da função de até .
Só tem um detalhe. não está definido no domínio dessa função, então tratamos de uma integral imprópria. Vou fazer a integral para um qualquer e depois calcular o limite quando :
Esse termo aí lembra a integral por substituição trigonométrica. Para esse formato a substituição deve ser . Vamos calcular a fórmula da integral e depois desfazemos a substituição e substituímos os limites de integração originais.
Passo 2
Resolvendo pela substituição trigonométrica:
Passo 3
Como originalmente, e sabemos que .
Assim, a função achada é essa aqui:
Agora calculando o limite de :
E essa é nossa área.