Área entre Curvas
Produzido por Arthur Melo de AlmeidaTeoria
O cálculo da área entre curvas é uma aplicação superimportante das integrais definidas! Bora conhecer!?
Como calcular a área entre duas curvas?
Como você calcularia a área hachurada na figura abaixo?
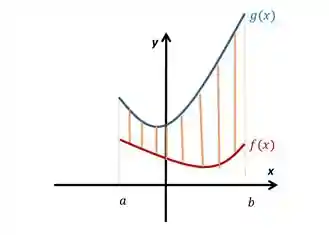
Podemos calcular essa área, fazendo a diferença entre a área sob a curva de cima,
Que é o mesmo que:
E é assim que calculamos a área entre curvas, sem mistério!
Beleza, mas foi tudo muito rápido! Agora vamos entender com mais calma 😉
Pra isso se liga nesse vídeozinho super completo com tudo o que você precisa saber sobre como usar a integral para calcular áreas entre curvas 👇👇👇
📢 Clique para saber mais:
Agora, continua comigo num passo a passo iradoso!
Passo a passo para calcular a área entre duas curvas
Dessa vez, vamos calcular a área englobada pela seguinte função, no intervalo
-Mas como assim, só tem uma curva?! 😵💫😵💫😵💫
Tem certeza?! Da uma olhadinha pro gráfico:
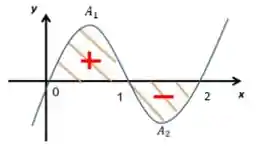
Uma parte do gráfico fica na parte negativa do eixo
-Ué? Mas como que minha área pode dar zero, tá certo isso?
Não! É exatamente aí onde entra a ideia de área entre curvas!
Se liga no pulo do gato! Nossas curvas vão ser:
Isso mesmo, o eixo
Bora pro nosso passo a passo então?!
Passo 1: Observar o comportamento das funções
Temos uma função de terceiro grau, então podemos assumir que ela tem no mínimo 3 raízes, e se todas forem reais, essa função cruza o eixo
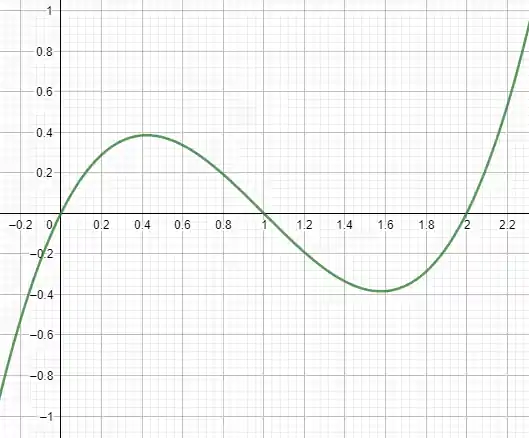
Resolvendo a equação é possível, verificar que essas raízes são
Passo 2: Reescrever as funções em uma função
Para descobrir a área, temos que calcular uma integral.
Show... Mas antes de sair calculando que nem um doido, observa que essa função, dentro do intervalo de
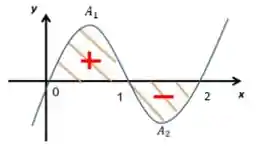
Então, ficamos com:
Na primeira parte da integral, a função
Já pra calcular a área
Substituindo:
Ficamos com:
Passo 3: Calcular a Integral
Nós sabemos que
Agora o problema se resume em calcularmos essas duas integrais. Ambas são integrais polinomiais e são bem simples de resolver. Depois da atenção com os limites de integração, temos como resultado:
Agora sim, área total positiva, tudo calculado certinho!
Exercício: Determine a área da região
A resolução desse exercício você encontra no vídeo abaixo 👇
Agora que você já aprendeu tudo sobre área entre curvas, bora treinar com mais exercícios?
Passo a passo para calcular a área entre duas curvas
Exercício: Determine a área da região , onde é a região limitada pela curva , pelo eixo , e pelas retas e .
Exercícios Resolvidos
Exercício Resolvido #1
UFF - Cálculo IIA - P1 Rodrigo Salomão 2012.2 – 1
Calcule a área da região compreendida entre o gráfico de
E o eixo , com
Passo 1
Po o primeiro passo é sempre tentar ver onde a curva está acima do eixo e onde está abaixo! O legal é tentar esboçar o gráfico. Aqui é um pouco complicado fazer isso, mas sabemos que essa função só se anula onde o numerador for 0, ou seja, .
Agora segue aqui comigo:
Então se for negativo, . Agora se for positivo, então . Então a gente pode pensar em algo assim:
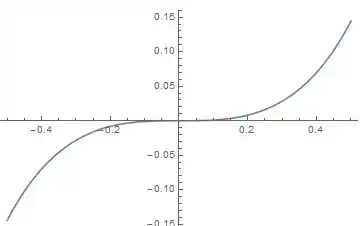
Repara que o denominador não pode zerar, e nele também temos uma raíz quadrada. Então a função não existe para . Porém como nosso limite de integração superior é , não vamos nos preocupar com isso.
Passo 2
Legal! Estamos vendo que a nossa área está acima do eixo , então vamos usar a seguinte fórmula:
Passo 3
Agora temos que resolver essa integral aí em cima. Essa integral sai por substituição trigonométrica, concorda? Vamos resolver a primitiva, voltar para e aplicar os limites de integração:
Bem, esse é o caso , .
Temos que fazer,
Substituindo na integral dada.
Passo 4
Agora, usando a substituição
Então a integral fica assim,
Voltando para :
Passo 5
Usando o triângulo retângulo para converter o na variável inicial:
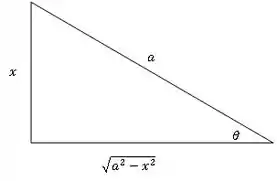
Então temos que
Passo 6
Agora vamos aplicar os limites de integração:
O que vai dar:
Resposta
Exercício Resolvido #2
UERJ - Cálculo 2 - Lista de Integrais Professora Renata - 32d
Determine a área da região , onde:
é a região limitada pela curva , pelo eixo e pelas retas e .
Passo 1
Primeiro eu vou pegar essa função e abrir melhor com o em evidência:
Olha, o tem raiz em . Já o não tem nenhuma raiz e é sempre positivo. Ou seja, ao que parece essa função do terceiro grau só tem raiz em e é negativa quando é negativo e positiva quando ele é positivo. Essas informações já são suficientes para esboçar algo assim:
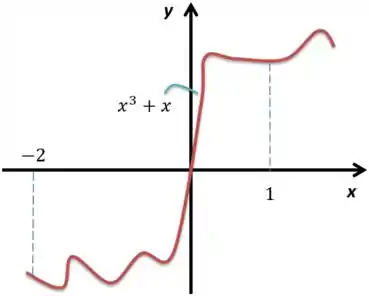
Passo 2
Olha lá uma parte em que está acima do eixo e outra que está abaixo. Então o que faremos? Vamos separar em duas regiões! A primeira está à esquerda do eixo e vamos chamar de e a segunda, que está a direita, vamos chamar de . Portanto,
Passo 3
Primeiro vamos analisar a área . Nessa área é menor que 0, então vamos fazer
Passo 4
Agora para a área aquela que está à direita do eixo , temos que a função é positiva. Então,
Passo 5
Agora a gente só precisa somar os dois resultados, ou seja
Resposta
Exercício Resolvido #3
Elaboração própria
Calcule a área delimitada entre as curvas:
Passo 1
Vamos lá desenhando a região primeiro. Vou começar pelo :
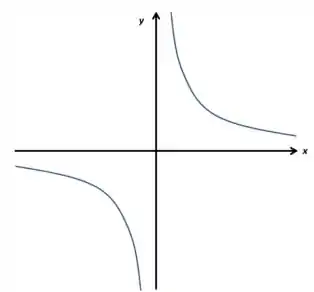
Bom, esse é o desenho base desse gráfico, que tem forma de hipérbole. Agora vou pensar em como encaixar os outros. Ora, tenho que ver aonde eles se interceptam! Primeiro o :
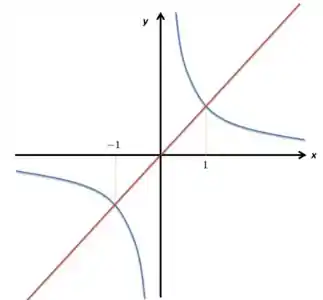
Agora, eu vou botar o outro, o :
Além de que ela toca a quando :
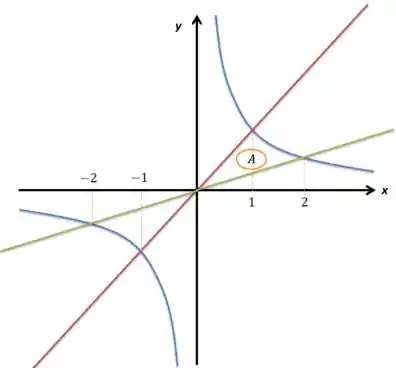
Então essa área entre os gráficos está aí marcada com . Lembrando que até teria uma outra área ali embaixo entre os gráficos, só que o cara especificou que .
Então, a integral está rolando de até , sendo que até o nós temos vermelho por cima e verde por baixo e a partir daí temos azul em cima e verde embaixo, ou seja:
Passo 2
Agora vamos integrar!
Resposta
Exercício Resolvido #4
Elaboração própria
Calcule a área delimitada entre as curvas:
Passo 1
Começamos desenhando as duas parábolas:
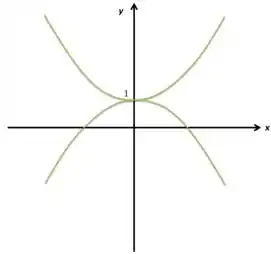
Ok, até aí sem muitos problemas. Agora que devemos encaixar aquela reta ali as devidas interseções. Bom, se você igualar esse gráfico ao gráfico da parábola superior, olha como fica:
Bom, se eu adicionar ainda o gráfico uma vertical paralela ao eixo passando em :
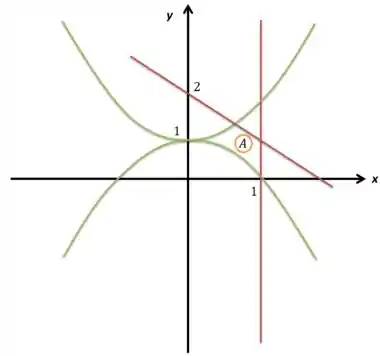
Já tenho ali a minha área definida, então.
Bom, agoraeu só preciso analisar o seguinte:
de até eu tenho a parábola de cima sobre a parábola de baixo
de até tenho a reta não vertical em cima da parábola de baixo. Assim:
Passo 2
Integrando uma de cada vez:
Passo 3
Agora a segunda parte
Passo 4
Juntando tudo
Resposta
Exercício Resolvido #5
PUC-RJ - Cálculo B - P1 2015.1 - 3
Considere a região delimitada pelas curvas e
Esboce a região .
Calcule a área da região .
Passo 1
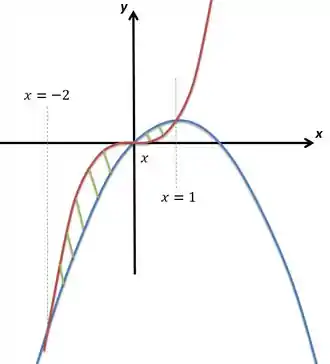
Para esboçar vamos primeiro reparar que um gráfico é , que vem de para e depois explode para , e o outro é , que tem raízes em e e tem concavidade para baixo, já que o termo que multiplica o é negativo. Vamos analisar a interseção dos gráficos:
Conluímos, assim, que a região será dividida em dois pedaços, um de a e outro de até . Vamos ao esboço:
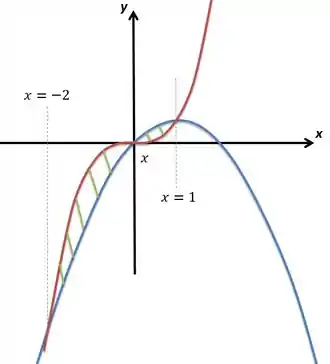
A região está pintada de verde.
Passo 2
Para calcular a área devemos montar uma integral com a diferença entre a função mais alta para a mais baixa. No intervalo a maior é a vermelha , em a mais alta é a azul :
Resposta
Exercício Resolvido #6
Elaboração própria
Calcule a área delimitada entre as curvas:
Passo 1
Vamos lá, existem gráficos que você precisa saber desenhar, como uma reta, parábola, seno, exponencial, etc.
Agora, existem os que você realmente não precisa, a exemplo desses dois aí em cima.
Nesses casos em que você não tem muita noção do que está se passando, você simplesmente escolhe um para ser sua e outro para ser sua .
Vê se você consegue visualizar: dependendo da ordem que você escolher essas funções você vai chegar na área ou em , se tiver escolhido a ordem contrária.
Dessa forma, só precisamos calcular em qualquer ordem e teremos como resultado o módulo da integral.
Bom, aquele me faz parecer que essa é a função maior, então vou tentar colocar ela como , mas tanto faz:
Passo 2
Bom, vamos integrar.
PARA TUDO!
Parceiro, me diz se isso aqui tá valendo:
Propriedade trigonométrica, né? Olha que bonito se eu fizer isso:
Caô? Tá de sacanagem? É, cara, o mundo é dos malandros:
Achei um valor para integral. Como eu disse, a área é o módulo dela (que no caso vai ser o próprio , já que é um valor positivo).
Resposta
Exercício Resolvido #7
UFRJ - Cálculo 1 - P2 2012.1 – 2
Seja a região limitada entre e o eixo . Encontre a equação da reta que passa pela origem e que divide em duas subregiões com áreas iguais.
Passo 1
Ora, ora. Problema interessante...
Foi nos dada uma função parabólica (do 2º grau e com concavidade para baixo). Essa curva e o eixo delimitam uma região de área . Vamos ver o seu gráfico?
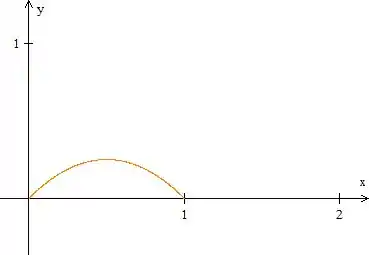
Queremos achar a equação de uma reta que passa pela origem.
Uma reta vai ser
Se ela passa na origem , então
No fundo, queremos calcular para que a área seja dividida pela metade
Passo 2
Vamos esboçar o que o enunciado nos diz:
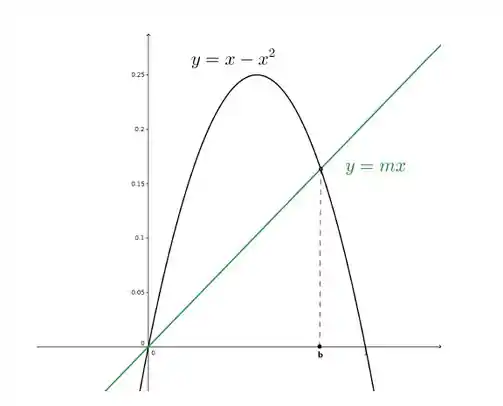
No desenho, foi desenhado uma reta genérica que corta .
OBS: Em problemas onde ainda não sabemos a equação de alguma curva, é muito útil esboçarmos uma situação genérica para essa curva e começar a fazer os cálculos a partir daí.
Igualando as equações, podemos achar os pontos de interseção:
Logo, .
Temos duas formas de prosseguir agora:
1. Dizendo que a área acima da reta é metade da área compreendida entre a parábola e o eixo .
2. Dizendo que a área acima da reta é igual a área abaixo dela.
Vamos seguir a forma 1, já que a área abaixo da reta é mais difícil de ser calculada (ou teríamos que integrar em relação a ou dividir em duas áreas).
Para isso é válido saber que a parábola intercepta em e .
Passo 3
Igualando a área acima da reta à metade da área abaixo da parábola, temos:
Assim, chegamos a uma equação para :
Logo, a equação da reta é:
Resposta
Exercício Resolvido #8
UFRJ - Cálculo 1 - P2 2011.2 – 3
Calcule a área da região limitada pelas curvas e . Faça um esboço da região.
Passo 1
O enunciado nos dá duas curvas:
O enunciado nos pede para esboçar a área limitada por essas curvas e calculá-la.
Para esboçar as curvas, vamos, primeiro entender melhor as funções dadas:
Isso é uma hipérbole. O gráfico vai ser algo assim
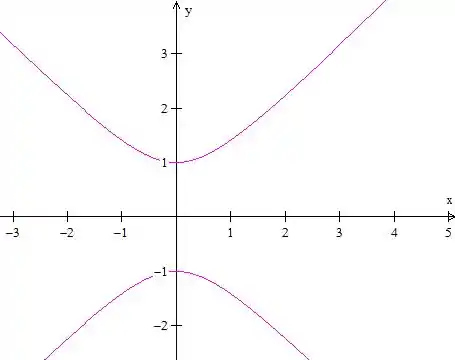
Mas repara que o é uma raiz quadrada, isso nos diz que ele é positivo, então vamos pegar só a parte de cima.
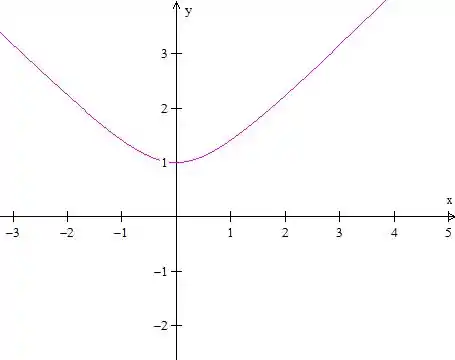
Passo 2
Agora vamos fazer
Ela vai ficar
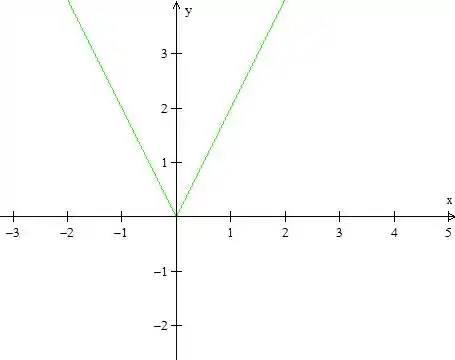
Agora que já podemos esboçar as funções, o próximo passo é igualar as suas equações para acharmos os pontos que elas se interceptam.
Depois, calcularemos a área da região limitada por elas através de integrais.
A nossa área vai ficar então
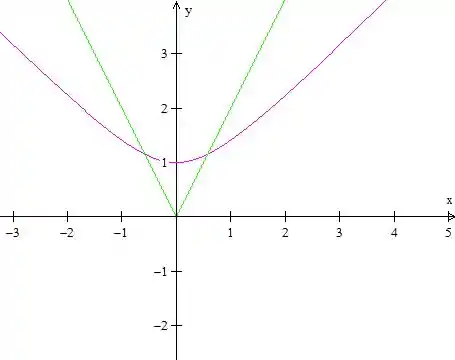
Entre o verde e o rosa.
Passo 3
Igualando as funções:
Esboço da região :
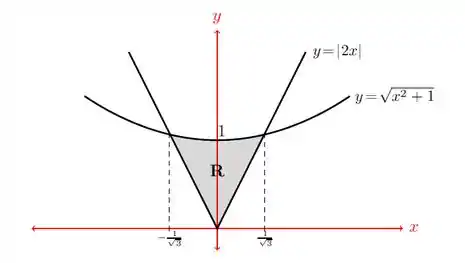
Pela simetria, podemos dizer que a área de é:
Passo 4
Vamos calcular a integral: .
Como aparece a expressão , vamos tentar a substituição trigonométrica:
Mudando os limites de integração:
Aplicando:
Passo 5
Resolvendo a segunda integral por partes:
Calculando:
Substituindo na expressão inicial:
OBS:
Nesse problema, o enunciado nos pediu explicitamente que teríamos que esboçar a região entre as curvas. Portanto, para fazer isso, tivemos que usar conceitos de derivada primeira e derivada segunda para acharmos a concavidade, ponto de mínimo, etc.
É bom estar com esses conceito frescos na hora da prova. Além disso, é bom saber equações de algumas curvas conhecidas:
Resposta
A área é da região é igual a