Área de Superfícies de Revolução
Produzido por Arthur Melo de AlmeidaTeoria
Eu sei que o nome assusta, mas vamos com calma.
Primeiro, uma superfície de revolução é uma superfície gerada quando giramos uma curva em torno de um eixo.
Por exemplo, a esfera é uma superfície de revolução. Se girarmos a função
Que é um semi-círculo de raio e centrado na origem, em torno do eixo , teremos a seguinte superfície resultante:
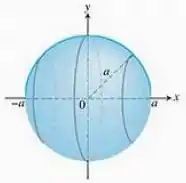
Rodando em torno do eixo
Se uma função é derivável num intervalo , então a área da superfície gerada pela rotação dessa função em torno do eixo é dada por:
Rodando em torno do eixo
Se uma função é derivável num intervalo , então a área da superfície gerada pela rotação dessa função em torno do eixo é dada por:
Só aplicação de fórmula! Mas vejamos isso aí na prática.
O segmento de reta é girado em torno do eixo , gerando o cone da figura abaixo. Vamos calcular a área superficial lateral desse sólido de revolução.
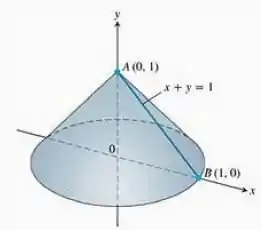
Uma observação importante: as fórmulas servem pra calcular só a área que foi gerada pela rotação. Ou seja, nesse caso é justamente o que ele quer: a área lateral do cone.
Caso ele pedisse a área externa toda do cone, teríamos que acrescentar a área da base, beleza?
Enfim, basta usar a fórmula com , e os intervalos de integração e :
Rodando em torno do eixo x
Rodando em torno do eixo y
Exercícios Resolvidos
Exercício Resolvido #1
George B. Thomas, Cálculo Volume II, 11ª ed. São Paulo: Pearson Education do Brasil Ltda., 2009, pp 477 –20
Determine as áreas das superfícies geradas pela rotação da curvas em torno dos eixos indicados.
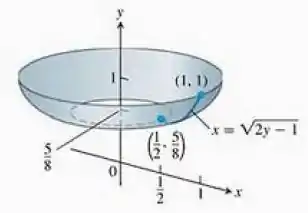
Passo 1
Queremos a área da superfície de revolução gerada pela rotação da curva em torno do eixo no intervalo . A função é derivável em todo o intervalo.
Portanto, tudo o que temos que fazer é utilizar aquela fórmula esperta de área usada para quando queremos a área da superfície lateral quando temos uma rotação em torno do eixo :
Passo 2
Vamos achar os elementos da integral.
Temos
Passo 3
Agora temos que resolver essa integral aí.
Olha só o que eu vou fazer. Vou juntar os dois termos que estão dentro da raiz:
Vamos dar uma arrumada nesse valor
Resposta
Exercício Resolvido #2
George B. Thomas, Cálculo Volume II, 11ª ed. São Paulo: Pearson Education do Brasil Ltda., 2009, pp 479 - 32
Determine a área de superfície gerada pela rotação, em torno do eixo , do pedaço de astróide , mostrado a seguir
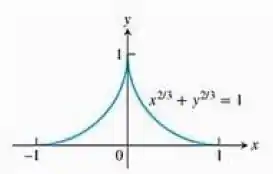
Dica: Gire o pedaço do primeiro quadrante em torno do eixo e dobre o resultado
Passo 1
Queremos a área da superfície de revolução gerada pela rotação da funçãoem torno do eixo . No enunciado, é dado o desenho da função, e podemos perceber que ela é simétrica.
Além disso, ele mesmo dá como dica calcular a área do sólido gerado pela rotação da função no primeiro quadrante e depois multiplicar por dois. A função no primeiro quadrante é:
Passo 2
Novamente, basta utilizamos aquela fórmula espertinha para calcular a área de uma superfície de revolução, gerada pela rotação de uma função em torno do eixo , lembrando que, nesse caso, a fórmula estará multiplicada por dois, pois estamos usando como a função do primeiro quadrante e ela daria apenas metade da área da figura formada, beleza? Por isso eu vou escrever assim:
Aí esse já vai ser a área da figura toda que eu quero \o/
Temos =
Passo 3
Agora temos que resolver a integral. Essa integral aí sai por substituição. Vou resolver a primitiva primeiro e depois aplicamos os limites de integração, pode ser?
Voltando para
Substituindo os limites de integração para calcular a integral definida:
Passo 4
Agora calculamos a área:
Resposta
Exercício Resolvido #3
George B. Thomas, Cálculo Volume I, 11ª ed. São Paulo: Pearson Education do Brasil Ltda, 2009, pp 478 –30a
Eis um desenho esquemático da redoma de pés usada pelo Serviço Meteorológico Nacional dos Estados Unidos para abrigar um radar em Bozeman, Montana.
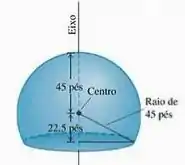
Se a redoma fosse pintada, qual a área da superfície que receberia tinta (sem contar a base)?
Passo 1
Queremos a área da superfície de revolução dada na figura. Primeiro temos que achar qual é a função que deu origem a essa superfície de revolução. Sabemos que o raio da redoma é .
Repara que temos a parte de uma esfera. A esfera vai ser a rotação de uma circunferência.
Então temos que achar a equação da circunferência que gera essa esfera
A equação de uma circunferência é dada por:
Nesse caso,
Vamos considerar o eixo sendo aquele eixo do desenho e o eixo passando pelo centro.
Agora olha bem para o desenho que ele deu. Essa superfície foi gerada pela rotação da circunferência com indo de até .
Então vamos rodar
Com
Passo 2
Novamente, temos que utilizar aquela fórmula espertinha para calcular a área de uma superfície de revolução, gerada pela rotação de uma função em torno do eixo .
A função que está sendo rotacionada é a função . Achamos essa função isolando o na equação da circunferência.
O nosso intervalo de integração será de a . Então temos:
Temos
Passo 3
Para resolver essa integral, vou fazer o seguinte:
Resposta
Exercício Resolvido #4
George B. Thomas, Cálculo Volume I, 11ª ed. São Paulo: Pearson Education do Brasil Ltda, 2009, pp 477 –8ª
Estabeleça uma integral para a área da superfície gerada pela rotação da curva dada em torno do eixo indicado
Com
Rotacionando em torno do eixo
Passo 1
Queremos a expressão da integral para calcular a área da superfície de revolução gerada pela rotação da função definida como
Em torno do eixo .
Novamente, basta utilizamos aquela fórmula espertinha para calcular a área de uma superfície de revolução, gerada pela rotação de uma função em torno do eixo :
Passo 2
Aqui, temos:
Nesse caso, para calcularmos vamos resgatar quem? Queeem? Isso mesmo, o teorema mais amado e idolatrado do Cálculo: o TFC!
Repara que ele só pede para obter a integral, ele não pede para calcular a área. Então não precisa se preocupar em encontrar um valor para a integral. A resposta é essa daí!! Acabooou!
Resposta
Exercício Resolvido #5
George B. Thomas, Cálculo Volume I, 11ª ed. São Paulo: Pearson Education do Brasil Ltda, 2009, pp 478 –31
a) A fórmula da área de superfície foi desenvolvida sob o pressuposto de que a função , cujo gráfico gerou a superfície, era não negativa no intervalo de integração. Para curvas que cruzam o eixo de revolução, substituímos a equação pela fórmula de valor absoluto
Use essa equação para determina a área de superfície do cone duplo gerado pela rotação, em torno do eixo , do segmento de reta ,
b) Determine a área de superfície gerada pela rotação, em torno do eixo , da curva
Passo 1
Queremos a área da superfície gerada pela reta em torno do eixo no intervalo . Nesse caso, como a função assume valores negativos e positivos no intervalo, iremos considerar o seu valor absoluto. Sem pânico. Acompanha aqui comigo que eu garanto ;)
Passo 2
Temos que usar a mesma fórmula que já utilizamos antes para calcular a área da superfície gerada pela rotação de uma função em torno do eixo :
Belezinha até aí?? Então repara só. Nesse intervalo de integração, que vai de a , a função assume valores positivos e negativos. Então ao invés de substituir ali por vou substituir por , beleza?
Passo 3
Para resolver, a primeira coisa que tenho que fazer é dividir os intervalos de integração:
No intervalo , e no intervalo de , . Portanto, escrevemos:
Passo 4
Queremos a área da superfície gerada pela curvaem torno do eixo no intervalo . Novamente, a função assume valores negativos e positivos no intervalo, iremos considerar o seu valor absoluto.
Passo 5
Vamos usar a nossa fórmula velha conhecida:
Como a função assume valores positivos e negativos no intervalo, vou substituir ali na fórmula por
Passo 6
Como a função é simétrica, podemos considerar o intervalo de em que a função é positiva e multiplicar por . Assim:
Passo 7
Para resolver a integral, utilizamos substituição simples:
Voltando para :
Passo 8
Passo 9
Olha o que aconteceria se eu ignorasse as barras de erro e substituísse os limites de integração simplesmente. Eu teria:
Daria zero porque a função é simétrica!