Cascas Cilíndricas
Produzido por Arthur Melo de AlmeidaTeoria
Quando aplicar o método das cascas cilíndricas?
Você sabia que podemos usar integral para calcular o volume de um sólido? Então, pensa num triangulo retângulo e agora rotacional ele em torno do eixo AB, como indicado na figura. Pronto, temos agora um sólido de revolução.
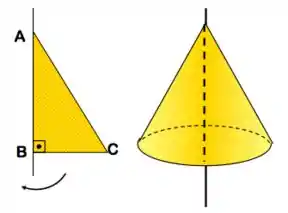
Tá, mas por que eu to te contando isso?
Porque nós usamos esse método, das cascas cilíndricas, pra calcular volumes de sólidos de revolução, que nada mais são do que sólidos obtidos pela rotação de uma figura em torno de algum eixo.
Não precisamos de integral pra calcular o volume de um cone né?
Agora suponha que queremos calcular o volume do sólido originado pela rotação, em torno do eixo , do gráfico de uma função ao longo de um intervalo :
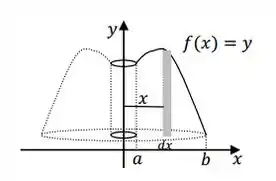
Vamos imaginar uma “casca” que está a uma distância do eixo , tem altura e uma espessura beeem pequena .
O volume da revolução dessa casca em torno de é:
Entendendo:
Logo, podemos integrar de a essa expressão e obteremos o volume que queremos:
Agora vamos para os exercícios praticar!
Exemplo...
Pensa na função e pelo eixo , com . E agora vamos calcular o volume do sólido de revolução obtido pela rotação dessa região em torno do eixo .
Bom, o gráfico é uma parábola, mas a região que a gente quer é só essa em vermelho:
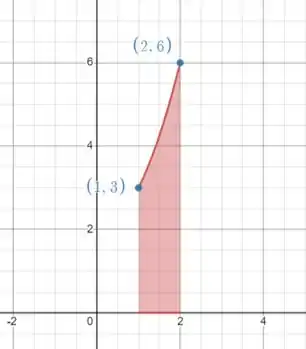
Aplicando a fórmula, o volume do sólido de revolução é
Agora é só desenvolver isso e integrar!
Pronto, o volume desse sólido de revolução é
Só umas observações...
Caso a função tenha sinal negativo no intervalo de integração, deve-se calcular:
Outra coisa: também podemos aplicar o método para curvas que giram em torno de :
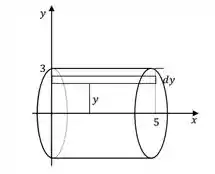
Repare: é o raio, é a espessura da casca e é a largura da casca.
Agora vamos para os exercícios praticar!
Exemplo...
Só umas observações...
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Considere a região delimitada pelo gráfico da função e pelo eixo , com .
Calcule o volume do sólido de revolução obtido pela rotação dessa região em torno do eixo .
Passo 1
Vamos começar visualizando essa região.
A função é bem simples, então podemos esboçar o gráfico dela:
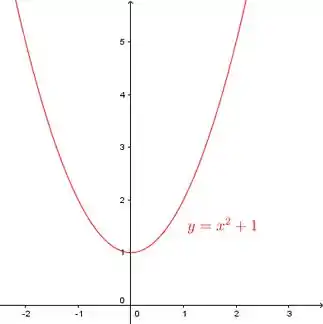
Mais especificamente, no intervalo , que foi o intervalo pedido:
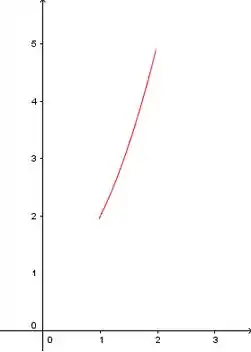
Então a região que o enunciado falou é:
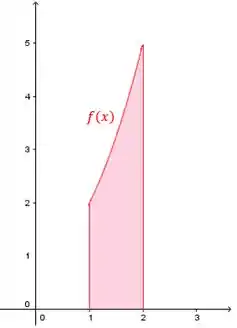
Passo 2
Aplicando a fórmula, o volume do sólido de revolução é
Passo 3
Agora é só desenvolver isso e integrar!
Resposta
Exercício Resolvido #2
PUC-RJ - Cálculo B - P1 2013.2 - 2
Encontre o volume obtido pela rotação da placa limitada por , , e , em torno do eixo , sendo .
Passo 1
O cara quer que nós calculamos o valor do volume rotacionado em torno de da região dada por:
Com e .
Vamos, em primeiro lugar, desenhar . Eu não sei com exatidão como se comportaria o num gráfico, mas deve ser algo parecido com um cosseno.
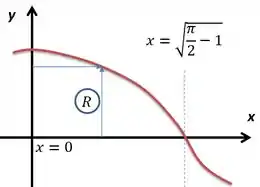
Ali eu representei também duas setas, uma horizontal e outra vertical. A horizontal vai medir em relação ao eixo o raio de rotação de em relação ao mesmo eixo. Já a seta vertical medirá uma distância do gráfico até o eixo . Enfim, como a rotação é em torno do eixo , podemos constatar que a reta horizontal medirá o raio dessa rotação e a vertical a altura. Fazendo o volume por cascas cilíndricas teríamos:
Passo 2
Vamos resolver a integral com uma substituição:
Esse é nosso volume!
Resposta
Exercício Resolvido #3
PUC-RJ - Cálculo B - P2 2014.2 - 4 bc
Considere a região delimitada pela parábola e pela reta .
Considere o sólido obtido pela rotação da região ao redor da reta . Escreva uma integral que calcule o volume de .
Calcule o Volume de .
Passo 1
Vamos começar fazendo o gráfico dessa parábola
Temos que a expressão da parábola pode ser melhor aberta por:
As raízes serão, para facilitar no seu desenho, aproximadamente e :
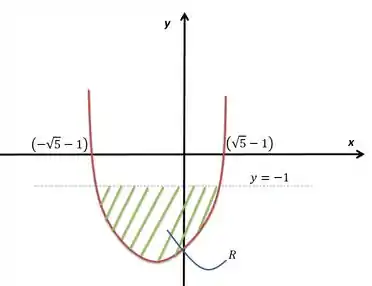
Lembrando que esse é apenas um esboço para dar uma noção geral.
Passo 2
Agora temos a área com o eixo de rotação para o volume
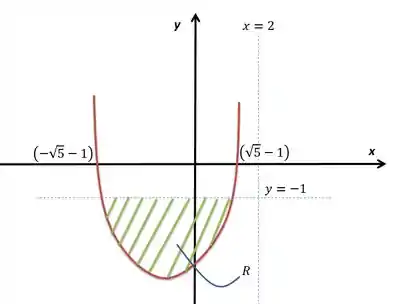
O método mais prático de fazer esse cálculo é através de cascas cilíndricas. Nesse caso, podemos dizer que a altura do cilindro será a distância da parábola até , ou seja
Para o raio, temos que ele valerá a distância horizontal de um ponto qualquer até um ponto na reta na mesma altura, ou seja, será a seguinte diferença:
Assim, nossa integral, que se estende no intervalo dos dois pontos onde encontra :
Terá sua integral dada por:
Passo 3
Agora é só resolver:
Resposta
Exercício Resolvido #4
UFRJ - Cálculo 1 - P2 2013.1 – 3
Seja a região situada entre as curvas , , e . Calcule o volume do sólido obtido fazendo girar a região em torno do eixo .
Passo 1
O chato dessa questão é conseguir visualizar. Vamos fazer um esboço para nos orientar. Como sabemos que o polinômio é crescente para todo o , podemos ver que:
Deve ser decrescente para todo , excluindo onde não está definido. Além disso temos:
Passo 2
Portanto podemos esboçar:
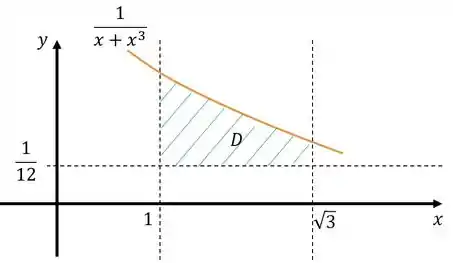
Agora podemos fazer a fórmula de cascas cilíndricas:
Onde é a distância de um ponto arbitrário no eixo até o eixo de giro. No caso a distância é simplesmente :
Passo 3
A função é a altura do gráfico. Como a região só considera a parte do gráfico acima de , nossa é:
Logo:
Passo 4
Fazendo a distributiva da integral:
Integramos:
Por fim, substituímos os valores:
Resposta
Exercício Resolvido #5
USP - Cálculo 1 - P3 2012 - 2 B
Seja a região compreendida entre os gráficos de e para , como mostra a figura abaixo:
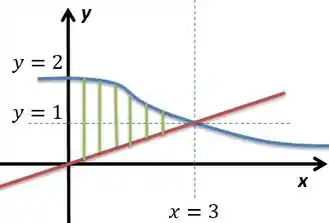
Calcule o volume do sólido obtido pela rotação de em torno de .
Passo 1
Giramos em torno do eixo . Vou tentar a integral por cascas cilíndricas, para não ter o trabalho de ter que inverter as funções e os limites de integração. Se fizermos assim, nós ficaremos com o volume sendo a rotação do gráfico azul menos a do gráfico vermelho em torno do eixo :
Os limites de integração são os mesmos, assim como as funções:
O primeiro termo da integral pode sofrer a seguinte substituição para ser resolvido:
Passo 2
Assim, sendo a outra integral a de um polinômio normal, ficamos assim: