Cálculo de Volumes – Discos e Anéis
Produzido por Arthur Melo de AlmeidaTeoria
Método dos Discos
Usamos esse método pra calcular o volume de sólidos obtidos pela rotação de alguma figura em torno de um eixo (os famosos sólidos de revolução).
Rodando em torno do eixo
Seja uma função contínua em .
Vamos considerar a região limitada pelo gráfico e pelas retas e .
O volume do sólido de revolução obtido pela rotação dessa região em torno do eixo é:
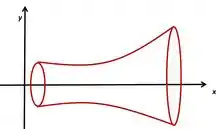
Isso vem da fórmula da área de um disco com raio , reparou?
Enfim, vejamos um exemplo.
Vamos calcular o volume do sólido de revolução obtido pela rotação, em torno do eixo da região limitada pela curva , pelas retas e .
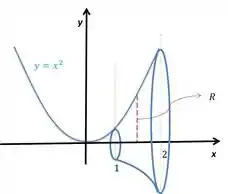
Basta aplicar a fórmula:
Rodando em torno de uma reta paralela ao eixo
Nesse caso o raio não é mais porque a distância ao eixo de revolução passa a ser a distância da curva até essa reta.
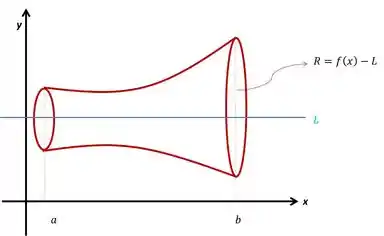
O volume do sólido de revolução obtido pela rotação da região em torno da reta é dado por:
Essa é a única diferença, o resto é só integrar igual!
Rodando em torno do eixo
Pra rotações em torno do eixo a fórmula fica no mesmo formato:
Vamos calcular o volume do sólido de revolução obtido pela rotação, em torno do eixo da região limitada pela curva , pelas retas e e .
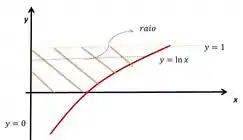
Repara que temos , mas na fórmula precisamos de um . Então temos que escrever em função de :
Show? Agora sim é só partir pro abraço!
Então fica a dica: às vezes você vai ter que reescrever a função antes de aplicar a fórmula. Agora vamos ver uns exercícios!
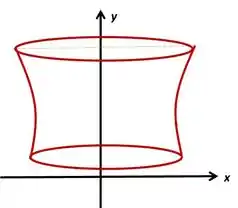
Método dos Anéis
A ideia desse método é bastante semelhante à ideia do método do disco. A diferença é que o método dos anéis é utilizado para quando giramos uma região limitada por duas curvas em torno de um eixo, ao invés de girarmos uma curva.
O eixo não é mais a fronteira da região que estou girando. Nesse caso, sempre haverá uma diferença de volumes. Complicou???? Nããão! Vamos lá!
Rotação em torno do eixo
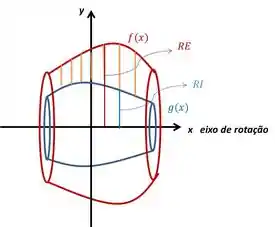
É um sólido com um buraco no meio. Nesse caso, sempre haverá uma diferença de volumes. O volume será dado pela diferença entre o volume da região maior e o volume da região menor. Basta descobrir os dois raios: o raio externo e o raio interno .
No caso em que estou simplesmente girando em torno do eixo , o raio externo será a função que está acima, no caso da figura, e o raio interno a função que está abaixo. No caso da figura, .
Exemplo: Encontre o volume do sólido obtido pela rotação, em torno do eixo da região limitada pelas curvas e e pelas retas e .
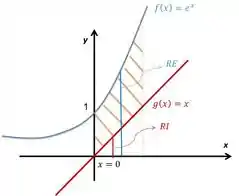
Rotação em torno de uma reta paralela ao eixo
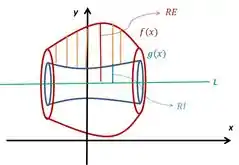
Nesse caso, essa reta passa a ser o eixo de revolução. Aí os raios externo e interno não são mais e porque a distância ao eixo de revolução passa a ser a distância de cada curva até essa reta . O que temos é o seguinte:
Rotação em torno do eixo
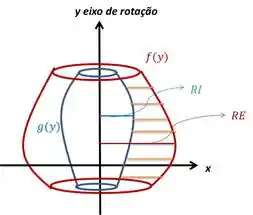
Nesse caso, a única coisa que muda é que ambas as funções têm que estar definidas em função da variável . Assim como no caso de volume de um sólido gerado pela rotação de uma região limitada por uma curva e o eixo, a variável independente tem que ser a mesma do eixo em relação em torno do qual faço a rotação.
Rodando em torno de uma reta paralela ao eixo x
Rodando em torno do eixo y
Método dos Anéis
Rotação em torno do eixo x
Rotação em torno de uma reta paralela ao eixo x
Rotação em torno do eixo y
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Calcule o volume do sólido de revolução obtido a partir da rotação de
Em torno do eixo .
Passo 1
Vamos esboçar isso aí antes de tudo. Vou traçar primeiro e , que são mais simples de serem desenhados. Aí substiuirei quando e .
O gráfico ficará assim:
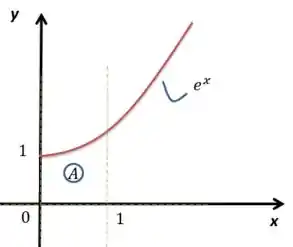
Aquele ali representa a área que eu vou girar em torno do eixo .
Bom, o raio de rotação da figura será , nesse caso. Então a integral a ser feita vai ser:
Passo 2
Integrando essa moleza aí:
E é isso, pessoal.
Resposta
Exercício Resolvido #2
UFF - Cálculo IIA – GMA – 2008.2 – Lista 6 – 15
Calcule o volume do sólido obtido pela rotação da região em torno do eixo , pelo método que achar mais conveniente.
Passo 1
Essa região na verdade são regiões, cada uma com sua função. Vamos separar em partes.
E calcular cada volume separado. Vamos ver
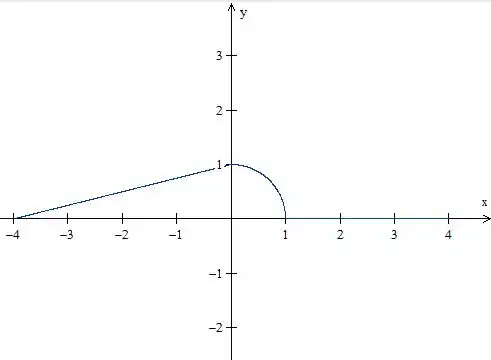
A grande dúvida aqui é qual dos métodos usar. Em todas as regiões temos , ou seja, uma função de que gira em torno do eixo . Então, vamos usar o método dos discos circulares.
Passo 2
Vamos começar pela região , os limite são os valores do intervalo, nesse caso e
Passo 3
Vamos para a região , os limite são os valores do intervalo, nesse caso e
Passo 4
O volume da terceira região vai ser zero, porque a função é , não tem nada para rotacionar aí
Passo 5
Então o volume total vai ser
Resposta
Exercício Resolvido #3
PUC-RJ - Cálculo B - P1 2013.1 – 3b
Seja a região limitada pelos eixos e pelo arco de parábola , para entre e .
Calcule o volume do sólido obtido girando a região acima em torno da reta
Passo 1
Vamos começar vendo como fica o gráfico dessa função, temos uma parábola com o coeficiente de negativo. Além disso, as raízes vão ser
A parábola vai ser
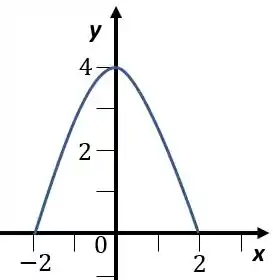
Mas ele só quer de à , então vamos ter
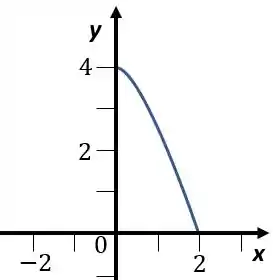
Passo 2
Para calcularmos o volume temos que entender que estamos com duas funções ali, uma que é
E outra que é
E vamos rotacionar essa área ao redor da reta
Vamos ver um desenho para nos ajudar
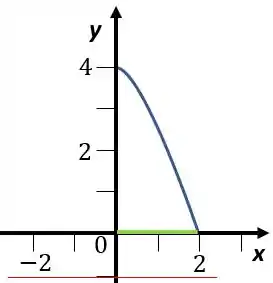
Vamos ver a fórmula para o cálculo de cada um dos volumes, como vamos rodar em torno de um eixo paralelo ao eixo vamos achar .
Primeiro da parábola em azul, a área vai ser
Colocamos aquele porque estamos rotando em torno dele.
O seu volume vai ficar
Passo 3
Vamos ao cálculo do outro volume, que é a rotação da reta verde.
A área vai ser
Colocamos aquele porque estamos rotando em torno dele.
O volume vai ficar
Passo 4
O volume total vai ser
Isso porque o volume de rotação da reta verde vai ser vazio.
Resposta
Exercício Resolvido #4
UERJ - Cálculo 2 - Lista de Integrais Professora Renata- 34e
Seja a região limitada pela curva e pelas retas e . Determine o volume do sólido de revolução gerado pela rotação de em torno, do eixo
Passo 1
Primeiro eu preciso desenhar a região:
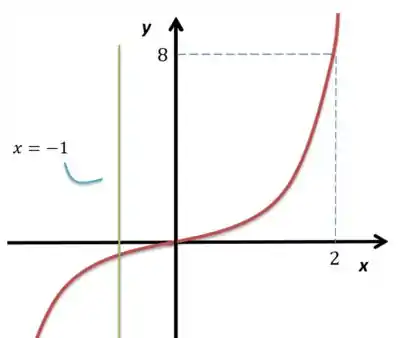
Repara que a área que eu estou trabalhando é essa entre o vermelho, o pontilhado do nível e o eixo . Bom, como vou integrar em , preciso da minha função em :
Agora integro no formato da integral para seções transversais. Repara só em uma coisa, minha função raio será a própria função , já que o eixo de rotação dista do eixo :
E aí, acabou? Não, é essencial que você não esqueça que entre o eixo e o de rotação fica um vácuo que você precisa levar em conta. Ele vai gerar um cilindro de raio e altura , ou seja:
O volume total da figura, então, é:
Resposta
Exercício Resolvido #5
PUC-RJ - Cálculo 1 - P3 2010.2 – 3
Determine o volume do sólido obtido pela revolução em torno do eixo-, da região limitada pelo gráfico de e no intervalo .
Passo 1
Vamos começar desenhando essa região, sendo que uma parábola tem boca para cima e seu vértice na origem e a outra tem boca para baixo e vértice em :
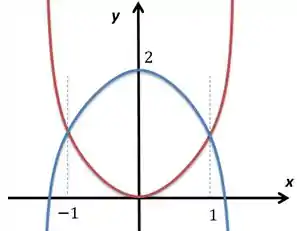
Eu aproveitei e já marquei o intervalo de bem onde as parábolas se encontram, repara aqui:
Legal até aí.
Passo 2
Agora a questão é ver como faremos essa diferença de rotações. Repara que na região delimitada em relação ao eixo de rotação, que é o eixo , a que está mais afastada é a parábola azul, ou seja, . A mais próxima é a vermelha, . Resumindo a brincadeira, vamos fazer a diferença da rotação da mais externa com a mais interna. Ficará assim, usando a fórmula de seções transversais:
Resposta
Exercício Resolvido #6
USP - Cálculo 1 - P3 2011.1 – 2
Determine o volume do sólido obtido pela rotação, em torno da reta , da região
Passo 1
Vamos começar desenhando a região e tentando definir de que área ele está tratando:
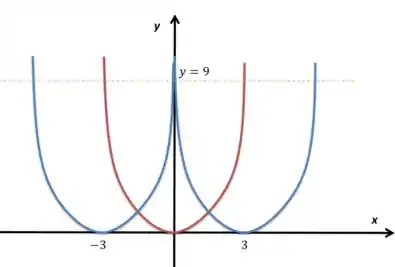
Bom, se você for procurar entender o espaço onde e , ficaríamos com a região dentro do vermelho (acima da linha vermelha) e abaixo da azul:
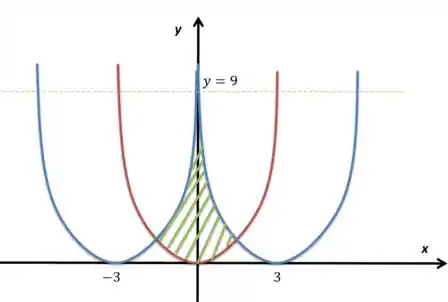
Essa região em verde é a que procuramos. Se trabalharmos as igualdades da parte vermelha com a parte azul da direita temos
E achamos
Se fizermos a outra igualdade, dessa vez da vermelha com a parte azul da esquerda temos
E achamos
A região que está girando vai ser separada em duas parte, uma a direita do eixo e uma a esquerda do eixo . A da direita vai ser o giro do menos o do no eixo , onde vamos ter indo de à .
A partira daí fazemos, no mesmo eixo, giro do menos o do , com entre e . Podemos então armar a operação:
Por simetria, podemos calcular só de um lado e multiplicar por , ou seja:
Resposta
Exercício Resolvido #7
Elaboração Própria
Calcule o volume do sólido gerado pela rotação de
Em torno de .
Passo 1
Primeiro vou esboçar a região:
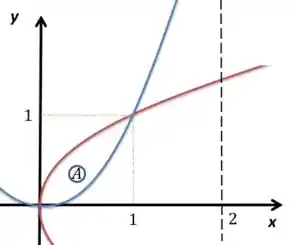
Bom, tenho que definir qual vai ser o meu raio de rotação nesse caso aí. Para o volume do sólido gerado na rotação do gráfico vermelho (, fica assim:
Pois, se é a distância do eixo até o gráfico e do eixo até a distância é , vale essa relação. Para o azul a mesma coisa:
Assim, o volume será dado pela resolução da integral:
Repara que com o giro em torno de uma reta paralela ao eixo eu integro em . Agora é conta.
Passo 2
Resposta
Exercício Resolvido #8
UFRJ - Cálculo 1 - P2 2010.1 – 5
Na figura abaixo, seja o ponto de interseção da curva e a reta , e seja o vértice da parábola . Suponha que a reta passa pelos pontos e .
Calcule o volume gerado pela rotação da região sombreada em torno do eixo-.
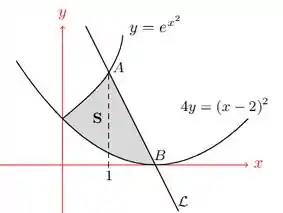
Passo 1
Temos o esboço da região a ser rotacionada em torno de , mas não temos a função da reta . Logo, isso é a primeira coisa que temos que achar.
A equação genérica da reta é dada por . Temos dois pontos pertencentes a reta e, tcharan(!), uma reta é definida por dois pontos. Logo, é só substituirmos o e pelas coordenadas dos pontos para acharmos a reta.
Depois, iremos calcular o volume de revolução. Repare que vamos ter que dividir a área em duas. Além disso, como queremos rotacionar em torno de , vamos usar as funções em função de e não de . Assim:
Passo 2
Achando as coordenadas de :
Achando as coordenadas de :
Achando a equação da reta :
Fazendo :
Logo:
Passo 3
Colocando as funções em função de :
Como , temos as seguintes curvas:
Vamos dividir a região em duas regiões da seguinte maneira:
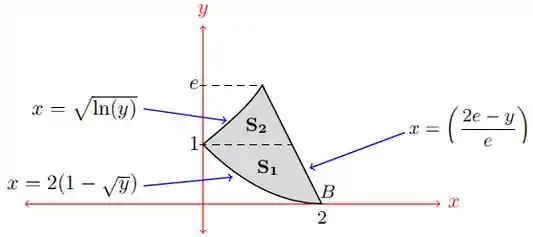
Passo 4
Vamos calcular através de integrais:
Vamos calcular a integral do final pelo método da integração por partes (repare que aparece uma função logarítmica e um ).
Substituindo em :
Calculando a área total:
Resposta
O volume é igual a