Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Valor Médio De Uma Função

Ver Todos os Exercícios

Teoria

Fala aí! Hoje vamos aprender como calcular o valor médio de uma função diferentona em um intervalo por meio de integrais, tá preparado?

Ah, importante! Aqui não vou tratar do Teorema do Valor Médio não, viu? Mas fica tranquilo, se for isso que você tá procurando, tem um textinho lá em Aplicações de Derivadas feito especialmente pra você 🥰

⭐ Veja também ⭐

Como calcular o valor médio de uma função?

Imagino que você tenha mais facilidade pra calcular a média de uma função desse tipo aqui:

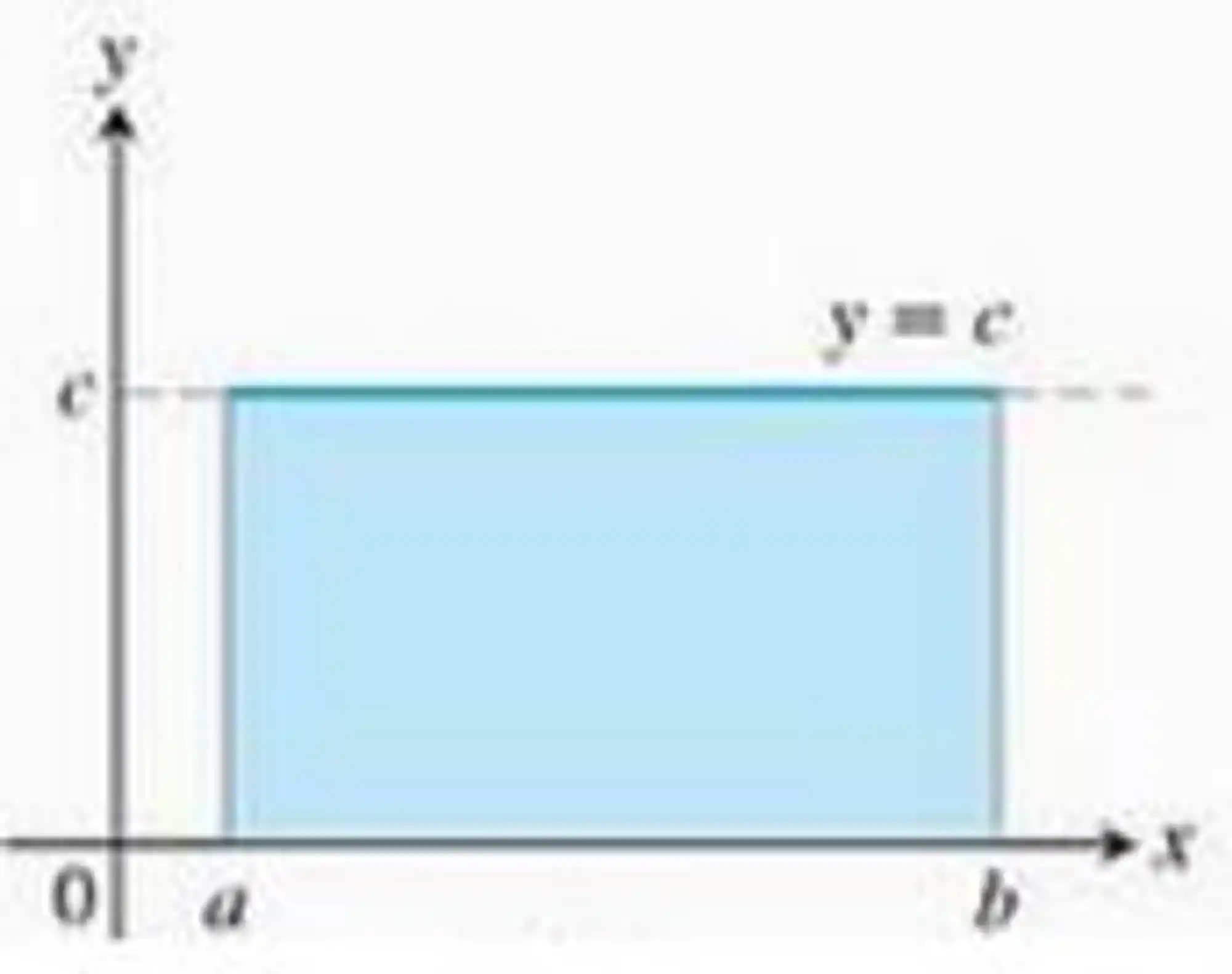
Gráfico de uma função constante
Gráfico de uma função constante

A média vai ser aquele próprio valor .

Mas e se você precisasse calcular a média de uma função como essa aqui?

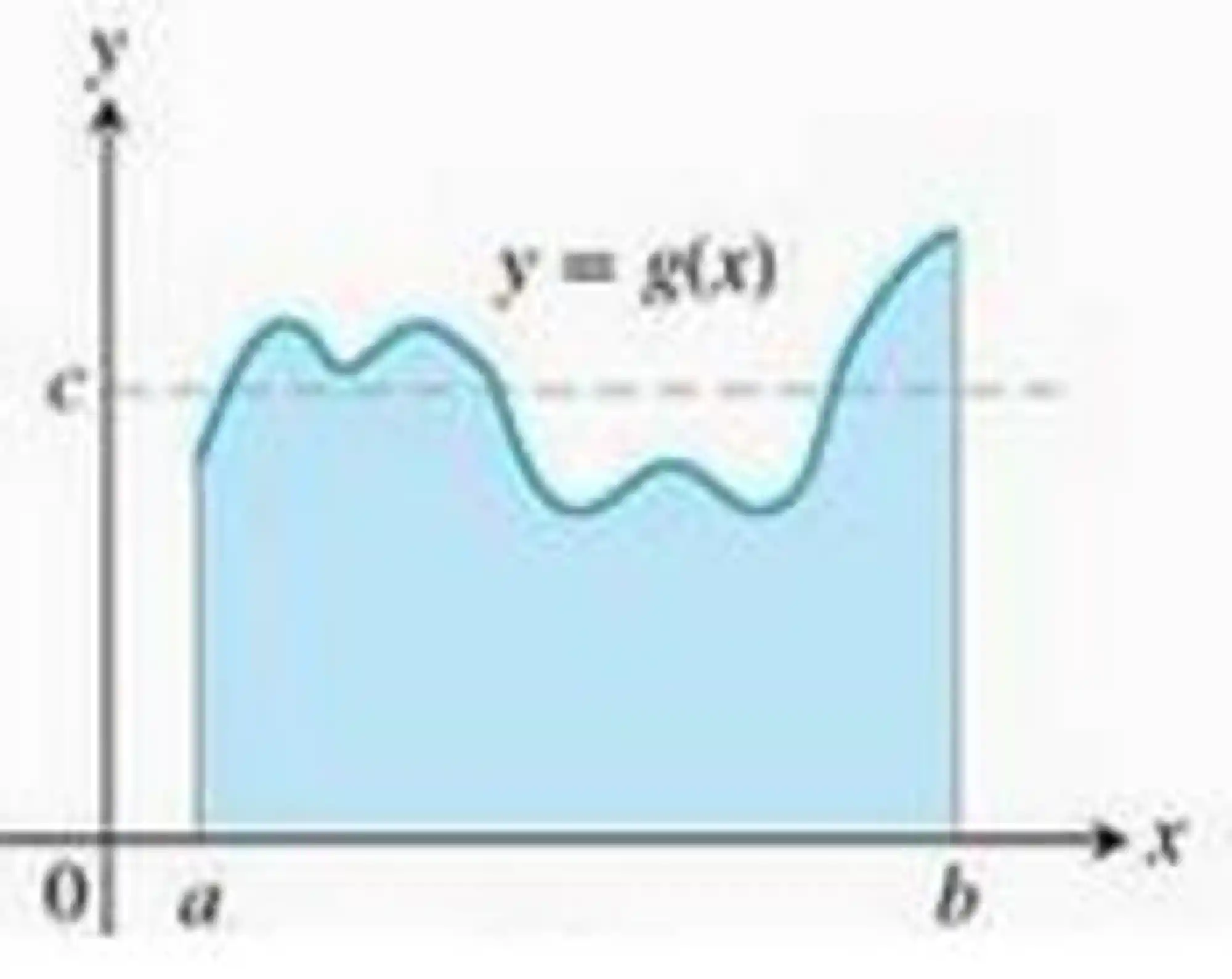
Gráfico de uma função
Gráfico de uma função

Aí já complica um pouquinho, né? Mas relaxa que já vamos aprender melhor.

Se preferir, pode até assistir esse vídeo bem curtinho aqui que te explico tudo o que você precisa saber. Senão, segue comigo no textinho logo abaixo 👇

Pensa no desenho daquele gráfico lá como a água em um tanque. A parede esquerda do tanque é representada por e a parede direita por .

Se balançarmos esse tanque, a água também balança e sua altura varia a cada ponto, concorda?

Mas a média dessa altura é sempre a mesma! Porque a quantidade de água dentro do tanque não muda.

Então, a gente pode interpretar essa média como a área limitada pela função dividida pelo intervalo .

Falou em área, falou em integral! Daí a fórmula para o cálculo do valor médio da função:

é

Bora ver como fica isso aí em um exemplo?

Exemplo: Calcule o valor médio da função no intervalo .

Galera, só aplicar a fórmula que acabamos de ver:

é

Quando aplicamos os limites de integração e fazemos as contas, chegamos em:

é

Tranquilo? Bora fazer mais alguns exercícios, então!

Exemplo: Calcule o valor médio da função no intervalo .

Exercícios Resolvidos

Exercício Resolvido #1

James Stewart, Cálculo Volume I, 6ª ed. São Paulo: Cengage Learning, 2010, pp 419 –1

Encontre o valor médio da função no intervalo dado

f x = 4 x - x 2 ,     0,4

Passo 1

Queremos o valor médio da função no intervalo dado. Tudo o que temos que fazer é utilizar a formulazinha esperta para calcular o valor médio de uma função.

V a l o r   m é d i o = 1 b - a   ∫ a b f x d x

V a l o r   m é d i o = 1 4 - 0   ∫ 0 4 4 x - x 2 d x

V a l o r   m é d i o = 1 4   4 x 2 2 - x 3 3 4 0

V a l o r   m é d i o = 1 4   4.16 2 - 64 3

V a l o r   m é d i o = 1 4   32 - 64 3 = 1 4 96 - 64 3

V a l o r   m é d i o = 8 3

Resposta

V a l o r   m é d i o = 8 3

Exercício Resolvido #2

James Stewart, Cálculo Volume I, 6ª ed. São Paulo: Cengage Learning, 2010, pp 419 – 7

Encontre o valor médio da função no intervalo dado

f x = cos 4 ⁡ x sen ⁡ x     [ 0 , π ]

Passo 1

Novamente, queremos o valor médio da função em dado intervalo. Vamos novamente aplicar a fórmula.

V a l o r   m é d i o = 1 b - a   ∫ a b h x d x

V a l o r   m é d i o = 1 π - 0   ∫ 0 π cos 4 ⁡ x   s e n   x d x

Passo 2

A integral

∫ cos 4 ⁡ x   s e n   x   d x

Sai pelo método da substituição simples:

u = c o s x → d u = - sen ⁡ x d x

s e n   x   d x =   - d u

∫ cos 4 ⁡ x   s e n   x   d x = ∫ - u 4   d u

= - u 5 5

Voltando para x :

∫ cos 4 ⁡ x   s e n   x   d x = - cos 5 ⁡ x 5

Passo 3

Agora podemos substituir os valores:

V a l o r   m é d i o = 1 π - 0   ∫ 0 π cos 4 ⁡ x   s e n   x d x

V a l o r   m é d i o = 1 π - cos 5 ⁡ x 5 π 0  

V a l o r   m é d i o = 1 π - cos 5 ⁡ x 5 π 0  

V a l o r   m é d i o = 1 π - - 1 5 5 - 1 5 5  

V a l o r   m é d i o = 1 π - - 1 5 - 1 5  

V a l o r   m é d i o = 2 5   π

Resposta

V a l o r   m é d i o = 2 5   π

Exercício Resolvido #3

James Stewart, Cálculo Volume I, 6ª ed. São Paulo: Cengage Learning, 2010, pp 419 – 14

Encontre os valores de b tais que o valor médio de f x = 2 + 6 x - 3 x 2 no intervalo 0 , b é igual a 3 .

Passo 1

Esse exercício aqui é um pouquinho diferente. Ao invés de te pedir o valor médio da função em um intervalo definido, ele te dá a média e quer saber em qual intervalo a função tem aquele valor médio.

No fundo, vamos usar a mesma fórmula do valor médio. Só que nessa caso, já vamos ter o seu resultado. A gente vai resolver em x , substituir b como um dos limites de integração e nossa incógnita será b . Acompanha aqui comigo!

V a l o r   m é d i o = 1 b - a   ∫ a b h x d x

V a l o r   m é d i o = 1 b - 0   ∫ 0 b 2 + 6 x - 3 x 2 d x

V a l o r   m é d i o = 1 b - 0     2 x + 6 x 2 2 - 3 x 3 3 b 0

V a l o r   m é d i o = 1 b     2 x + 3 x 2 - x 3 b 0

Sabemos que v a l o r   m é d i o = 3

3 = 1 b     2 b + 3 b 2 - b 3

3 = 2 + 3 b - b 2

b 2 - 3 b - 2 =   - 3

b 2 - 3 b + 1 = 0

Utilizando a famosa fórmula de Bhaskara para resolver a equação do segundo grau acima:

b = 3 ±   9 - 4 2 = 3 ± 5 2

As duas raízes são positivas, então as duas são válidas \o/

Resposta

b = 3 ± 5 2

Exercício Resolvido #4

James Stewart, Cálculo Volume I, 6ª ed. São Paulo: Cengage Learning, 2010, pp 419 – 22

A velocidade v do sangue que circula em uma veia com raio R e comprimento l a uma distância r do eixo central é

v r = P 2 η l R 2 - r 2

Em que P é a diferença de pressão entre as extremidades da veia e η é a viscosidade do sangue.

Encontre a velocidade média (em relação a r ) no intervalo 0 ≤ r ≤ R . Compare a velocidade média com a velocidade máxima.

Passo 1

Esse exercício pode assustar um pouco. Mas na verdade ele é igual aos outros. Ele está pedindo a média de uma função, só que a diferença é que está contextualizado, ou seja, ao invés de ser uma função qualquer em função de x que ele inventou, é uma função que tem um significado físico.

Aquelas letras todas ali assustam, mas se você reparar, ele quer a média da função v em função de r no intervalo [ 0 , R ] . A variável da função é r e todas as outras letras são constantes. Olha só o que tenho que fazer:

V a l o r   m é d i o = 1 b - a   ∫ a b v r d r

V a l o r   m é d i o = 1 R - 0   ∫ 0 R P 2 ƞ l R 2 - r 2 d r

V a l o r   m é d i o = 1 R   P 2 ƞ l ∫ 0 R R 2 - r 2 d r

V a l o r   m é d i o = 1 R   P 2 ƞ l     R 2 r - r 3 3 R 0

V a l o r   m é d i o = 1 R   P 2 ƞ l     R 3 - R 3 3

V a l o r   m é d i o = 1 R   P 2 ƞ l     2 R 3 3

V a l o r   m é d i o =   P   R 2 3 ƞ l    

Passo 2

Ele pede ainda para compararmos o valor médio da função no intervalo com seu valor máximo. A função é decrescente no intervalo [ 0 , R ] , de modo que seu valor máximo nesse intervalo ocorre em r = 0 . Em r = 0 , a função vale:

v m á x =   v 0 =   P 2 ƞ l R 2 - 0 2 =   P R 2 2 ƞ l

Para compararmos a média com o valor máximo, fazemos:

v m é d i o v m á x = P   R 2 3 ƞ l P R 2 2 ƞ l = 1 3 1 2 = 2 3    

v m é d i o = 2 3 v m á x

Resposta

V a l o r   m é d i o =   P   R 2 3 ƞ l    

v m é d i o = 2 3 v m á x

Exercícios de Livros Relacionados

Use o diagrama para mostrar que se f é côncava para cima em [ a , b ] , então f m e df a - b 2
Encontrar a massa total e o centro de massa de uma barra de 5 m de comprimento, sabendo que a densidade linear num ponto é uma função do 1º grau da distância total desse ponto ao extremo direito da ba
(a) Encontre o valor médio de f no intervalo dado.(b) Encontre c tal que f m e d = f ( c ) .(c) Esboce o gráfico de f e um retângulo cuja área seja a mesma que a área sob o gráfico de f. f x = x - 3 2
Use o resultado do Exercicio 77 na seção 5.5 para calcular o volume médio de ar inalado pelos pulmões em um ciclo respiratório.
Ache o valor de χ que satisfaz o teorema do valor médio para integrais para a integral a seguir. Faça uma figura ilustrando a aplicação do teorema. ∫ 1 2 x 3 = 15 4