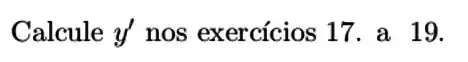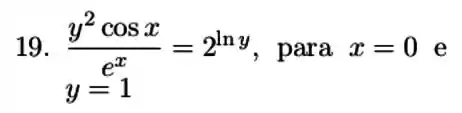Exercícios de Derivação Implícita - Lista de Exercícios Resolvida

O fólio de Descartes

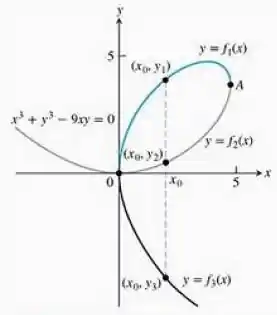
Encontre o coeficiente angular do fólio de Descartes, nos pontos e

Em qual ponto, além da origem, o fólio tem uma tangente horizontal?

Encontre as coordenadas do ponto da figura, onde o fólio tem uma tangente vertical.

Encontre a derivada no ponto da curva definida implicitamente abaixo:

Encontre no ponto diferenciando implicitamente a curva definida por

Se , encontre o valor de no ponto .

No exercício, use a derivada implícita para determinar .

1. Usando derivação implícita, encontre uma equação da reta tangente à curva no ponto .

P1. Em cada item:

(1) determine implicitamente,

(2) encontre explicitamente,

(3) derive o resultado obtido em (2) para encontrar em termos de ,

(4) substitua y encontrado em (2) na expressão encontrada em (1) e verifique que a resposta é consistente com o (3).

Em cada item:

(1) determine implicitamente,

(2) encontre explicitamente,

(3) derive o resultado obtido em (2) para encontrar em termos de ,

(4) substitua y encontrado em (2) na expressão encontrada em (1) e verifique que a resposta é consistente com o (3).

Encontre a reta tangente à curva no ponto . Admita que a referida curva define implicitamente como função diferenciável de em algum intervalo aberto contendo e de forma que .

Se uma função, derivável em , que é dada implicitamente por . Quanto vale e ?

Encontre no ponto diferenciando implicitamente a curva definida por

Determine a expressão de pelo menos duas funções definidas implicitamente pela equação . Explicite seus domínios.

Considere definida implicitamente por . Calcule , sabendo que para todo pertencente aos reais.

Use derivação implícita para encontrar a equação da reta tangente à curva

no ponto

Considere a curva definida, implicitamente, pela equação

Ache o coeficiente angular da reta tangente a essa curva no ponto .

24. Use derivação implícita para calcular nos itens a seguir:

b)

24. Use derivação implícita para calcular nos itens a seguir:

c)

24. Use derivação implícita para calcular nos itens a seguir:

e)

24. Use derivação implícita para calcular nos itens a seguir:

f)

24. Use derivação implícita para calcular nos itens a seguir:

h)

24. Use derivação implícita para calcular nos itens a seguir:

g)

24. Use derivação implícita para calcular nos itens a seguir:

j)

24. Use derivação implícita para calcular nos itens a seguir:

k)

Calcule de

Calcule de

Seja uma função derivável definida em um intervalo aberto centrado em e dada implicitamente pela equação:

Qual é o valor de ?

Seja uma função que satisfaz a equação , qualquer que seja . Então, a equação da reta tangente ao gráfico de no ponto é

Dado que:

Prove que

1. Em cada item: (1) determine implicitamente, (2) encontre explicitamente, (3) derive o resultado obtido em (2) para encontrar em termos de , (4) substitua encontrado em (2) na expressão encontrada em (1) e verifique que a resposta é consistente com o (3).

c.

3. Suponha que é uma função que satisfaz a equação

Encontre uma reta tangente à curva acima num ponto , com , e que seja paralela à reta .

1. Em cada item: (1) determine implicitamente, (2) encontre explicitamente, (3) derive o resultado obtido em (2) para encontrar em termos de , (4) substitua encontrado em (2) na expressão encontrada em (1) e verifique que a resposta é consistente com o (3).

d.

Em cada item:

(1) determine implicitamente,

(2) encontre explicitamente,

(3) derive o resultado obtido em (2) para encontrar em termos de ,

(4) substitua y encontrado em (2) na expressão encontrada em (1) e verifique que a resposta é consistente com o (3).

Encontre por derivação implícita.

Encontre por derivação implícita.

Considere como a variável independente e como a variável dependente e use a derivação implícita para encontrar , sabendo que

Se e , encontre

Seja a função definida implícitamente pela relação em um intervalo contendo . Então, é igual a:

Calcule .

Calcule .

Considere definida implicitamente por . Calcule , sabendo que para todo pertencente aos reais.

Encontre , se é definida implicitamente pela equação

Calcule .

Calcule:

Suponha que é dada implicitamente pela equação . Suponha que .

Calcule .

24. Use derivação implícita para calcular nos itens a seguir:

a)

24. Use derivação implícita para calcular nos itens a seguir:

d)

8. Se , encontre o valor de no ponto onde .

24. Use derivação implícita para calcular nos itens a seguir:

i)

Usando o teorema da função implícita, encontre da função a seguir

Usando o teorema da função implícita, encontre da função a seguir

Usando o teorema da função implícita, encontre da função a seguir

Usando o teorema da função implícita, encontre da função a seguir

Usando o teorema da função implícita, encontre da função a seguir

Usando o teorema da função implícita, encontre da função a seguir

7. Uma escada de está encostada em uma parede. Se a extremidade inferior da escada for afastada do pé da parede a uma velocidade constante de , com que velocidade a extremidade superior estará descendo no instante em que a inferior estiver a da parede?

8. Uma partícula se desloca ao longo da parábola no primeiro quadrante de modo que sua coordenada (medida em metro) aumente a uma velocidade constante de . Qual é a derivada em relação ao tempo do ângulo de inclinação da reta que liga a partícula à origem quando .

Prove:

Se então

6. Sabeno que o ponto pertence à curva e que a equação da reta tangente à curva nesse ponto é dada por , determine e .

Encontre por derivação implícita.

Calcule a derivada se

10. A Regra da Potência pode ser demonstrada usado a derivação implícita para o caso onde é uma número racional, , e é supotar antemão ser uma função derivável. Se , então . Use a derivação implícita para mostrar que

Para cada equação determine .

h)

Expresse em termos de e , onde é uma função derivável dada implicitamente pela equação:

a)

Expresse em termos de e , onde é uma função derivável dada implicitamente pela equação:

f)

Expresse em termos de e , onde é uma função derivável dada implicitamente pela equação:

d)

Expresse em termos de e , onde é uma função derivável dada implicitamente pela equação:

e)

Encontre para cada uma das curvas abaixo:

Expresse em termos de e , onde é uma função derivável dada implicitamente pela equação:

c)

Suponha que seja uma função derivável e dada implicitamente pela equação

Mostre que em todo no domínio de com .

Expresse em termos de e , onde é uma função derivável dada implicitamente pela equação:

b)

Seja para . Escreva e derive implicitamente para confirmar para . Aplique o processo análogo à função , para , para confirmar que para .

Se , então o valor de no ponto onde é

5. Seja uma função diferenciável tal que, para todo , o ponto é solução da equação . Sabendo que , calcule .

Encontre , se é definida implicitamente pela equação dada

A função , com , é dada implicitamente por . Determine a equação da reta tangente ao gráfico de , no ponto de abscissa .

2. a) Calcule no ponto sendo definida implicitamente pela equação

b) Calcule a derivada da função

11. (1EE-2019.2) Considere a curva dada por .

(a) Determine uma expressão para em termos de e .

Calcule , se

Obtenha sabendo que .

Considere na equação e determine:

(a)

(b) a derivada

(c) a equação da reta tangente ao gráfico de no ponto

Dada a equação e , calcule quando

(a)

(b)

(c)

(d)

(e)

P1. Em cada item:

(1) determine implicitamente,

(2) encontre explicitamente,

(3) derive o resultado obtido em (2) para encontrar em termos de ,

(4) substitua y encontrado em (2) na expressão encontrada em (1) e verifique que a resposta é consistente com o (3).

2. Encontre por derivação implícita.

c.

5. Seja uma função diferenciável tal que, para todo , o ponto é solução da equação . Sabendo que , calcule .

2. Encontre por derivação implícita.

d.

4) Suponha que é derivável e . Sabendo que e , calcule .

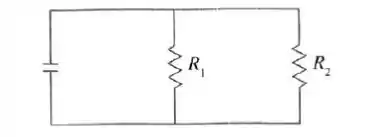
Se dois resistores com resistências e estão conectados em paralelo, como na figura, então a resistência total , medida em ohms (, é dada por

Se e estão crescendo a taxas de e , respectivamente, quão rápido estará variando quando e ?

2. Encontre por derivação implícita.

b.

1. Em cada item: (1) determine implicitamente, (2) encontre explicitamente, (3) derive o resultado obtido em (2) para encontrar em termos de , (4) substitua encontrado em (2) na expressão encontrada em (1) e verifique que a resposta é consistente com o (3).

c.

1. Em cada item: (1) determine implicitamente, (2) encontre explicitamente, (3) derive o resultado obtido em (2) para encontrar em termos de , (4) substitua encontrado em (2) na expressão encontrada em (1) e verifique que a resposta é consistente com o (3).

d.

2. Encontre por derivação implícita.

Dê o que se pede:

1. Determine as constantes tais que:
2. Prove ou dê um contraexemplo:

“Seja uma função definida e derivável em todo . Se a derivada de for contínua, então é derivável até segunda ordem em todo ”.

Encontre se .

Seja E a elipse de equação . Existem 2 retas tangentes a E que passam pelo ponto (12,3). Encontre as equações dessas retas.

Considere o Folium de Descartes

(a) Ache um vetor tangente e um vetor normal ao Folium de Descartes em .

(b) Ache equações paramétricas da reta normal ao Folium de Descartes em .

(c) Esta reta normal passa pela origem? Justifique.

Determine uma função que satisfaça à relação

A função é derivável e satisfaz à equação

Calcule

Seja dada implicitamente por . Suponha que seja derivável.

Calcule e a reta tangente ao gráfico de no ponto .

Calcule a derivada de.

Se então existe? Se sim, calcule

Seja , com . Se é a inversa de , mostre que

3. Determine todos os pontos do plano complexo nos quais a função dada por é derivável. Caso seja derivável, calcule sua derivada.

Considere a curva definida pela equação .

(a) Calcule .

Encontre para cada uma das curvas abaixo:

Encontre para cada uma das curvas abaixo:

Encontre

b)

Encontre uma equação da reta tangente e normal à curva no ponto .

Encontre

a)

Encontre

c)

Questão 4 - A superfície de um cubo oco, de aresta , é feita de um material que se encolhe uniformemente a uma taxa constante de . Determine com que taxa está diminuindo o volume do cubo no momento em que sua aresta mede .

Se uma função, derivável em , que é dada implicitamente por . Quanto vale e ?

3.35. (P1-2016) Seja uma função derivável definida em um intervalo aberto centrado em e dada implicitamente pela equação . O valor de é

a)

b)