Derivadas Laterais
Produzido por Arthur Melo de AlmeidaTeoria
Calculando o valor da Derivada antes e depois do ponto
Assim como temos limites laterais, as funções também possuem derivadas laterais. No exemplo abaixo, observe:
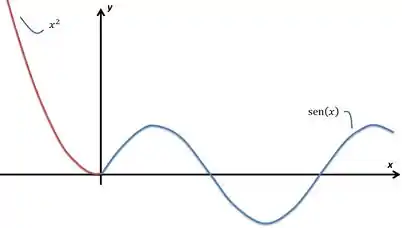
Essa função é dada por:
Como derivamos em ? Precisamos de uma análise lateral dessa derivada, que pode ser feita de duas formas!
Continuidade Derivação de funções:
Uma vez que você saiba que a função é contínua no ponto estudado, (tem que mostrar isso na questão, hein?!) você pode derivar os termos dos dois lados e ver se batem no mesmo valor.
Assim, calculamos as derivadas laterais derivando as funções de cada um dos lados.
Começando para esquerda de :
Agora fazemos pela direita de :
Definição da derivada no ponto:
Aplicamos a definição da derivada no ponto, por limite, e calculamos lateralmente os limites. Por exemplo, pela esquerda temos:
Pela direita, temos:
Repara que a derivada lateral é a derivada analisada por cada lado em que aproximamos de um ponto.
Como calcular a derivada usando limite pode não ser tão simples, sempre opte pelo primeiro método, a não ser que a questão peça pela definição.
Agora vamos praticar!
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
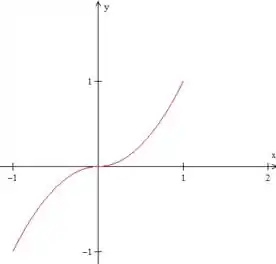
Calcule as derivadas laterais de no ponto .
Passo 1
Repara, a função é contínua em , como vemos no gráfico. Portanto, para achar as derivadas laterais dessa função nesse ponto basta derivá-las de primeira, pelo método da teoria.
Passo 2
A derivada pela esquerda, em relação ao ponto , vai ter como fórmula o seguinte:
Como :
Passo 3
A derivada pela direita, em relação ao ponto , vai ter como fórmula o seguinte:
Como :
Resposta
Exercício Resolvido #2
Elaboração prória
Sendo a função
Calcule as derivadas laterais de no ponto .
Passo 1
Vamos ver se esse cara é contínuo em . Se for, derivamos lateralmente, ou seja, precisamos verificar se:
Passo 2
Primeiro vamos calcular o limite pela esquerda
Observa que é definida pela mesma expressão , ou seja,
Passo 3
Agora vamos calcular o limite pela direita
Portanto, contínua em ! Vamos derivá-lo lateralmente agora.
Passo 4
A derivada pela esquerda, em relação ao ponto , vai ter como fórmula o seguinte:
Como :
Passo 5
A derivada pela direita, em relação ao ponto , vai ter como fórmula o seguinte:
Como :
Resposta
Exercício Resolvido #3
Elaboração própria
Sendo a função
Determine para que as derivadas laterais de sejam iguais
Passo 1
Vamos ver se esse cara é contínuo em . Se for, derivamos lateralmente, ou seja, precisamos verificar se:
Passo 2
Primeiro vamos calcular o limite pela esquerda
E depois, pela direita:
Observa que é definida pela mesma expressão , ou seja,
Sendo assim:
Passo 3
A derivada pela esquerda, em relação ao ponto , vai ter como fórmula o seguinte:
Como :
A derivada pela direita, em relação ao ponto , vai ter como fórmula o seguinte:
Como :
Passo 4
Pras derivadas laterais então serem iguais, fazemos:
Opa, então conseguimos achar !
Resposta
Exercício Resolvido #4
Elaboração própria
Sendo a função
Calcule as derivadas laterais de no ponto .
Passo 1
Vamos ver se esse cara é contínuo em . Se for, derivamos lateralmente, ou seja, precisamos verificar se:
Passo 2
Primeiro vamos calcular o limite pela esquerda
Observa que é definida pela mesma expressão , ou seja,
Passo 3
Agora vamos calcular o limite pela direita
E aí pra gente calcular esse limite vai depender da gente lembrar quem é a tangente hiperbólica. Pra dar uma refrescada na memória:
Sendo assim, o limite fica:
Portanto, contínua em ! Vamos derivá-lo lateralmente agora.
Passo 4
A derivada pela esquerda, em relação ao ponto , vai ter como fórmula o seguinte:
Como :
Passo 5
A derivada pela direita, em relação ao ponto , vai ter como fórmula o seguinte:
E como vimos, com , a tangente hiperbólica tem valor . Logo:
Resposta
Exercício Resolvido #5
Elaboração própria
Sendo , calcule as derivadas laterais de no ponto .
Passo 1
Ué, perai, essa função não é definida por partes, as derivadas laterais vão ser com certeza iguais.

Pêêêêêêê
Não tão rápido meus caros. Isso ai não vai ser necessariamente verdade. O jeito da gente descobrir se é ou não e fazer a questão direito é lembrar da definição de módulo e aplicar nessa função. Veja bem:
Então pra nossa função, vamos ter:
Ou ainda:
E ai sim conseguimos trabalhar. Então partiu!
Passo 2
Vamos ver se esse cara é contínuo em . Se for, derivamos lateralmente, ou seja, precisamos verificar se:
Primeiro vamos calcular o limite pela esquerda
Observa que é definida pela mesma expressão , ou seja, E, agora, vamos calcular o limite pela direita:
Portanto, contínua em ! Vamos derivá-lo lateralmente agora.
Passo 3
A derivada pela esquerda, em relação ao ponto , vai ter como fórmula o seguinte:
Como :
Já a derivada pela direita, em relação ao ponto , vai ter como fórmula o seguinte:
Como :
Ou seja, a nossa função até era contínua, mas não possuía derivadas laterais iguais em