Diferenciabilidade de Funções Definidas por Partes
Produzido por Arthur Melo de AlmeidaTeoria
Funções que mudam sua lei de formação: São contínuas? Como derivá-las? Onde habitam? De que se alimentam? Hoje, no Globo Repórter.
Saque o exemplo que motiva essa teoria:
Para derivar as funções, precisamos que elas sejam diferenciáveis. Aqui está o cerne da questão!
Se as funções dadas são contínuas dentro dos seus domínios, podemos derivar expressão por expressão, mas faltará analisar os pontos em que a função muda de lei de formação. No exemplo, isso acontece em e .
Se você aplicar a definição de continuidade, verá que a função do exemplo é sempre contínua. Assim sendo, podemos usar as derivadas laterais. Derivando primeiro:
Agora verificamos as derivadas laterais:
As derivadas não bateram! Então, a função não é derivável aí em ! Pegando agora :
Boa, em , as derivadas bateram, logo será diferenciável aqui, valendo .
Juntando tudo que concluímos, teremos:
Repare que os e foram substituídos por e e descrevemos pontualmente a derivada onde a muda a sua formação.
Derivando o módulo
Pessoal, esse é um momento único na vida de qualquer aluno de engenharia. Vocês vão ver a derivada da função módulo, tipo essa aqui:
Tá, forcei um pouco? Não é tão emocionante assim! Mas, como fazemos para derivar essa criança ai?
Cara, primeiro precisamos retirar esse módulo para podermos trabalhar com funções que sabemos derivar.
Como que tira essas barrinhas dos infernos? Basta lembrar da definição de módulo. Ou seja, ele vale ele mesmo quando for maior que zero e vale seu oposto quando for menor que zero.
Não lembrava onde o argumento do módulo era maior que zero? Basta acompanhar o desenho aqui
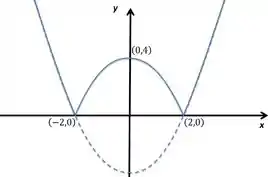
Nos pontos onde há mudança de função, e , temos as raízes de . Dessa maneira, podemos derivar a função chaveada nos dois domínios (em e em ), tendo o cuidado de usar a definição da derivada para observá-la nos pontos de mudança na lei de formação de .
Começando nesses pontos, procuramos:
Calculando os dois, acharemos que seus limites laterais não batem.
Vemos que nesses “bicos” que a função modular gera no seu gráfico (olha de novo como a função fica no gráfico ali de cima) ela não tem derivada.
Importantíssimo: Sempre que tivermos um ponto de mudança da lei de formação da função modular gerando esse “bico”, ou seja, com derivadas laterais diferentes de , a derivada não existirá nesse ponto.
Funções definidas no ponto
Cara, as vezes o enunciado te dá uma função que é desse tipo aqui:
Que muda de expressão em .
Quando você estiver com um caso desse, basta testar a continuidade da função no ponto em que ela muda de expressão. Se ela for continua nesse ponto, será derivável ali e como a outra expressão é derivável sempre a será derivável em todo o lugar.
Partiu exercícios!
Derivando o módulo
Funções definidas no ponto
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria.
Derive a função abaixo:
Passo 1
Bom, como a função tem expressões diferentes para e , precisamos analisar separadamente a sua derivada para cada um desses valores.
Começando com . Para esses pontos, temos:
Vamos aplicar então, as regras de derivação nisso aí.
Passo 2
Aplicando a regra do produto:
Passo 3
Agora, aplicamos a regra da cadeia em :
Para .
Passo 4
Temos que calcular as derivadas laterais em para ver se elas são iguais e diferentes de aí nesse ponto. Vou pelo método . Começamos verificando se ela é contínua no ponto:
Temos
Logo, sim, a função é contínua!
Falta ver se é derivável.
Passo 5
Derivando, teremos a mesma função dos dois lados, que já achamos no Passo :
Substituindo , temos:
Isso nos dá que:
Resposta
Exercício Resolvido #2
UFF - Cálculo IA – GMA – 2008.2 – Lista 6 – 16
Derive cada função (se possível, simplifique a função e/ou a derivada da função).
Passo 1
A derivada desse cara vai ser a derivada da função, feita pelos métodos de derivação convencionais, para , somada à análise de sua possível derivada em .
Passo 2
Assim, começamos calculando essa derivada para valores fora de (com a Regra do Produto e da Cadeia):
Passo 3
Olhamos agora para . Vamos ver se a função é contínua e derivável nesse ponto, fazendo as derivadas laterais pelo método .
Começamos com a continuidade:
Indeterminação dentro do seno? Vamos usar o Teorema do Confronto!
Logo,
Do enunciado temos que:
É contínua! Ótimo, falta provar só se podemos derivá-la
Passo 4
Vamos na derivação agora. Do passo tínhamos:
Em a função não está definida, pois dá ruim. Porém, podemos aplicar o teorema do confronto, vem comigo!
Para a primeira parcela, temos
Já para a segunda parcela,
Assim,
Então, a função será derivável em ! Teremos nesse ponto.
Passo 5
Organizando tudo, teremos a derivada de dada por:
Resposta
Exercício Resolvido #3
UFF - Cálculo IA - P2 Sérgio Almaraz 2010.1 – 2 b
Considere
Determine a derivada de
Passo 1
Observando a lei de definição de percebemos que exceto nos pontos e , é composta por funções deriváveis em seus domínios. A saber, , , (para ). E sabemos que a subtração, multiplicação e composição de funções deriváveis é derivável.
Então, os únicos candidatos a ponto onde a função é não derivável são e . Portanto, temos que analisá-los.
Passo 2
Vamos começar observando se são contínuas nesses pontos:
Portanto, a função é contínua nos dois pontos.
Passo 3
Dado isso, podemos fazer as derivadas das funções e ver se elas convergem lateralmente
Derivamos cada pedaço da função:
Em temos:
Derivável em !
Em temos:
Não será derivável em !
Passo 4
Assim, juntando essas derivadas à definição da derivada no ponto , teremos:
Note que a derivada não está definida para . Note ainda que se substituirmos na expressão ou na expressão temos como resultados que é o valor da derivada no ponto .
Resposta
Exercício Resolvido #4
Elaboração Própria
Seja a função tal que
Calcule .
Passo 1
A primeira coisa quando nos deparamos com uma função com módulo é sempre reescrever ela sem o módulo. E pra isso temos que analisar o sinal do que está dentro do módulo:
Podemos ver que
Passo 2
Ou seja, a função pode ser escrita assim:
Passo 3
Pronto, agora é só derivar normal! Então vamos ter:
Resposta
Exercício Resolvido #5
Elaboração própria
Seja .
Esboce o gráfico de
Dê os pontos onde é duas vezes diferencial e determine e .
Passo 1
Vamos desenhar o gráfico desse módulo de parábola. O processo deve ser desenhar a própria parábola, descobrindo suas raízes e depois “espelhando” toda a região abaixo do eixo para cima.
Descobrindo as raízes da parábola, teremos:
Como essa parábola tem concavidade para cima, a gente sabe que a parte negativa dela está entre suas raízes, e . Com isso, espelhando essa região teremos esse gráfico:
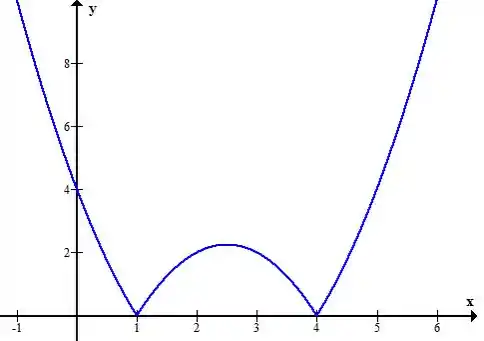
Passo 2
Onde essa função será diferenciável? Repara, o polinômio, quando está fora do módulo, é sempre derivável para quantas vezes quisermos. Quer dizer, se a função fosse só nós saberíamos que ela é derivável sempre, para todos os reais, na derivada primeira, segunda, terceira, ... -ésima derivada.
O problema do módulo é gerar dois “bicos” ali que complicam para a primeira derivada e, portanto, para a segunda derivada, terceira e por aí em diante.
Logo, quais são os únicos pontos em que e não estão definidos?
Logo, é duas vezes diferenciável para todo real menos e : .
Passo 3
Para derivar a função, onde ela pode ser derivável duas vezes, começamos abrindo em forma de módulo:
Derivando esse cara, teremos:
Com isso
Passo 4
O mesmo para a segunda derivada.
Juntando isso em forma de chave, teremos:
Resposta
Exercício Resolvido #6
Hamilton Luiz Guidorizzi, Um curso de Cálculo Vol. 1, 5ª ed. Rio de Janeiro: LTC, 2001, Pg 162 exercício 1f
Determine , e , onde
Passo 1
Temos uma função definida em intervalos diferentes, isso é importante para fazer as derivadas. Para derivá-la, precisamos ver onde ela será derivável.
Em se tratando de polinômios, eles são deriváveis em todo o seu domínio. Com isso, o problema vai morar sempre em . Temos que observar se aí ele será derivável ou não, e podemos fazer isso analisando as derivadas laterais pelo método apresentado na teoria de Derivadas Laterais.
Passo 2
Vamos começar fazendo a continuidade:
Contínua!
A boa é derivar a função agora e ver se as derivadas laterais batem:
Aplicando às derivadas laterais, ficamos com:
É, a derivada aí converge para .
A nossa derivada vai ser
Passo 3
Já vimos que a derivada primeiro converge para um valor. Se queremos derivar a função
Pelo mesmo método do Passo precisamos que a função a ser derivada, seja contínua em para depois derivá-la lateralmente. Já vimos que a derivada primeiro converge para um valor, . Com isso, já podemos derivá-la e analisa-la lateralmente
Não sei ainda se existe derivada em , por isso não o coloquei ali
Aplicando às derivadas laterais, ficamos com:
Não dão o mesmo resultado, então não será derivável em
Vamos ter como resultado final
Passo 4
Agora vamos para a terceira derivada, lembra que a terceira derivada é derivar ? Então tudo isso que pensamos antes vai valer do mesmo jeito, nos dois intervalos que ele definiu fazemos a derivada normalmente.
Só que dessa vez não vamos fazer a terceira derivada em , isso porque sempre que uma derivada não existe, ela não vai existir para nenhuma ordem depois dela.
Não entendeu? Não existe segunda derivada para , isso vai nos dizer que não existe terceira derivada nesse ponto, nem quarta derivada, nem quinta, nem sexta, nem sétima e por aí vai. Entendeu? Não temos um valor para usar na definição, então ele também não existe.
Vamos ter derivando, portanto:
Resposta
Exercício Resolvido #7
USP - Cálculo 1 - P1 2011 – 2 b
Seja a função definida por
Determine os pontos em que é derivável. Justifique.
Calcule nos pontos em que é derivável.
Passo 1
Usamos a continuidade lateralmente para observar suas derivadas laterais, calculadas pelo método apresentado na Teoria de derivadas laterais.
Trabalhamos, nas duas regiões de , com funções contínuas. Pode procurar, não há indeterminações ou pontos em que as funções explodam para nos seus domínios.
Pra variar, o nosso problema para ver a continuidade está simplesmente no ponto onde troca o domínio: . Vamos observar a continuidade nele.
Passo 2
Fazemos seus limites laterais:
Usando o Teorema do Confronto:
Assim,
Como os limites laterais não batem, ela não é contínua nem derivável em .
Passo 3
Agora precisamos derivar a função para observar sua continuidade no resto do domínio:
A primeira, para , é mais tranquila:
Essa derivada vale para com . Sim, esse é um ponto em que a derivada da função não será contínua em algum ponto. Nesse caso, vemos que a derivada não existirá em , pois esse valor gera , já que zeraria o denominador ali.
Passo 4
Para o domínio a derivada vai dar mais trabalho, vamos ter que usar a regra do Produto, do quociente e da cadeia, todas juntas:
É, esse monstro enorme é nossa derivada...
E então, por incrível que pareça, nenhum valor de vai zerar denominador nessa derivada ou gerar qualquer tipo de indeterminação, de onde a gente conclui que ela não gera problemas para a derivada.
Passo 5
Agora temos que achar as derivadas.
Mas repara, acabamos de calcular elas! Para :
Para e diferente de :
Sendo que em e em ela não existe.
Resposta
Exercício Resolvido #8
USP - Cálculo 1 - P1 2012 - 2 c
Seja
Seja . A função é derivável em ? Por que?
Passo 1
Analisando as derivadas laterais pelo método , usamos a definição:
Passo 2
Pelas propriedades dos limites, separamos esse cara em dois.
Passo 3
Esse limite que sobrou pode sair pelo Limite Fundamental Trigonométrico:
Passo 4
Assim,
Chegamos a uma constante! Assim garantimos que é derivável em .