Modelagem - MHS
Produzido por Carolina SabaTeoria
Aplicações a Física
Fala aí, tatuí!!! Agora que já sabemos resolver EDO’s de 2ª Ordem homogêneas com coeficientes constantes, vamos utilizar isso para resolver problemas físicos. Os principais tipos de problemas que vamos abordar aqui são:
- Movimento Harmônico Simples (MHS): Sistema Massa-Mola
- MHS: Pêndulo Simples
- MHS: Pêndulo Físico
Vamos ver cada um deles, passo a passo, a fim de treiná-los em relação à modelagem de problemas físicos, pois, nesse tipo de problema, a parte que apresenta maior dificuldade é conseguir montar a equação diferencial corretamente a partir das informações fornecidas no enunciado.
Movimento Harmônico Simples(MHS):Sistema Massa-Mola
Movimento harmônico é qualquer movimento que tenha a cara de seno, cosseno ou combinação entre eles, ou seja, a movimentação do corpo respeita uma relação de seno ou cosseno, vamos ver isso na prática!!!
Quando a gente tem só uma mola e um bloquinho, o sistema é esse aqui (repare que não tem atrito envolvido):
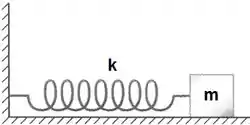
O sistema está em movimento e a massa oscila em torno da posição de equilíbrio.
Vamos encontrar uma equação que descreva o movimento do corpo.
Imagine que alguém pegou essa massa e deu uma puxadinha nele e largou! O sistema entrou em movimento. Como não tem atrito envolvido, esse corpo vai oscilar para sempre! Vamos ver como isso fica?
Analisando as forças atuantes no bloco em um instante genérico temos:
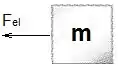
Só temos a força elástica (normal e peso se anulam). Logo, a força resultante é a força elástica. Então:
Pela Lei de Hooke:
Repare que é negativa pois tem direção contrária ao deslocamento da massa, ou seja, quando você desloca a massa para frente, ela aplica força para trás!
Logo:
Pronto!
Agora é só substituir na Segunda Lei de Newton:
Só que a aceleração é a derivada segunda da posição:
Onde:
Substituindo:
Passando tudo para o mesmo lado:
Dividindo tudo por :
Sempre que a gente tiver esse sistema, a gente vai encontrar essa equação. É com ela com que você tem que se preocupar!
Vamos escrever com a cara que estamos acostumados:
A gente chama de, a gente precisa dele para achar a frequência de oscilação do sistema será dada por . Logo o período de oscilação do sistema é dado por
Então temos:
Portanto, chegamos a uma EDO de segunda ordem homogênea de coeficientes constantes! Já sabemos resolvê-la! A equação auxiliar é:
Logo . Usando a fórmula de Bhaskara temos:
Então, a solução geral será:
MHS Pêndulo Simples:
Outro exemplo de Movimento Harmônico Simples (MHS) é o pêndulo Simples
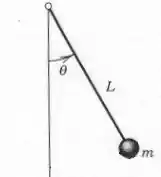
Vamos fazer um passo a passo para mostrar o raciocínio que iremos utilizar
Passo 1: diagrama de corpos livres e forças atuantes.
Isolando a massa, temos o seguinte:
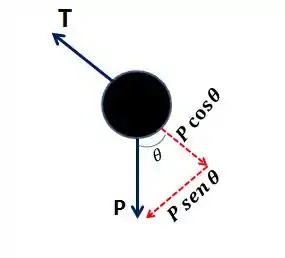
Passo 2: encontrar força resultante.
Como não há movimento na direção do fio, podemos decompor o peso nessa direção e na direção do movimento, perpendicular (setas pontilhadas).
Então a força resultante é dada por:
Passo 3: aplicar a Segunda Lei de Newton:
Sabemos que , mas no caso do pêndulo, temos que:
Veja a figura abaixo para melhor entendimento.
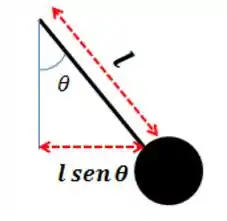
Esse seno tá atrapalhando nossa vida, não é?
Mas para pequenos valores de :
Observação: apareceu um seno, fala que o ângulo é pequeno e substitui o seno pelo próprio ângulo.
Então:
Derivando duas vezes:
Passo 4: chegar à equação do MHS
Substituindo na Segunda Lei de Newton:
De novo, vamos usar a aproximação para pequenos valores de :
Logo:
Comparando com a equação do MHS:
Percebeu que tem exatamente a mesma cara do nosso primeiro exemplo? Pois é, é só resolver um, que é o mesmo estilo de resolução para todos os outros!
MHS: Pêndulo Físico
Outro exemplo é o pêndulo físico!
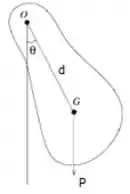
Nesse caso, temos um corpo de massa e momento de inércia , preso a um eixo em um ponto cuja distância ao centro de massa é .
Vamos ao passo-a-passo:
Passo 1: diagrama de corpos livres e forças atuantes.
Temos um par de ação e reação nessa massa. Então a força resultante é zero!
E agora?
Agora a gente usa a Segunda Lei de Newton para rotação:
Onde é o torque resultante, é o momento de inércia e é a aceleração angular.
Vamos calcular o torque em relação ao ponto do eixo, ou seja, o ponto que não se move:
Passo 2: encontrar torque resultante:
Como o torque que calculamos é o único que atua no corpo, então:
Passo 3: aplicar a Segunda Lei de Newton:
Como
Para pequenos valores de :
Então:
Perceba que essa EDO tem a mesma “cara” que as outras EDO’s que encontramos para o sistema-massa mola e o pêndulo simples.
Importante: não precisa decorar isso. Só estamos fazendo pra você pegar o “feeling” de como montar e resolver a equação do MHS, beleza?
MHS Pêndulo Simples:
MHS: Pêndulo Físico
Exercícios Resolvidos
Exercício Resolvido #1
UNA - Mecânica Aplicada - Vibrações Mecânicas
Um oscilador harmônico possui massa e período de vibração natural, medido em um osciloscópio, igual a . Determinar a constante de mola.
Passo 1
Pois bem, para começarmos um problema como esse, acho melhor eu e você entendermos o como um todo, e esse será o nosso primeiro passo:
Temos que determinar a constante de mola de um oscilador harmônico equivalente a um sistema massa-mola. Podemos determinar isso, lembrando que mola tem a ver com frequência, e a frequência natural de um sistema harmônico massa mola é dada por:
E é daí que vamos tirar a constante de mola !
Passo 2
Toda frequência angular, é medido se tivermos um período através da maravilhosa igualdade:
Como no nosso caso . Só que temos que converter para segundos. Isso é tranquilo, lembrando que ...
Portanto...
Passo 3
Finalmente podemos substituir tudo na equação da frequência natural de um sistema massa mola:
Elevando ambos os lados ao quadrado:
Resposta
Exercício Resolvido #2
UERJ - Cálculo 3 - Lista 6 Fernando Lopes - 1
Exercício nº 1 letra lista 6 de Cálculo III – IME - UERJ – Prof. Fernando Lopes C. -2014
Resolva o sistema de oscilações
Passo 1
Vamos usar a segunda lei de Newton para conseguir montar a equação diferencial.
Mas para isso, precisamos fazer o diagrama de forças.
Analisando as forças atuantes no bloco em um instante genérico temos:
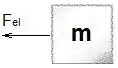
Só temos a força elástica (normal e peso se anulam). Logo, a força resultante é a força elástica.
Passo 2
Então, pelo diagrama de forças atuantes temos:
Porém, pela Lei de Hooke:
Logo:
Substituindo na Segunda Lei de Newton:
Que é o mesmo que:
Onde:
Passo 3
A equação característica dessa EDO é:
Logo
O que evidencia que a solução tem a carona de:
Da pra juntar esses dois caras em um só:
E tchã!Fechou clã! Isso vale para o pêndulo físico e o pêndulo simples! O que muda em cada um deles é o !
Resposta
Exercício Resolvido #3
Encontre a solução da equação do pêndulo simples de comprimento e condições iniciais:
Passo 1
Vamos partir da equação do pendulo simples:
Substituindo os valores encontramos:
Essa EDO é simples de resolver. A solução da equação é da forma:
Agora vamos resolver normalmente o PVI.
Passo 2
Calculando a derivada:
Igualando as condições iniciais, temos:
Substituindo na equação temos:
Resposta
Exercício Resolvido #4
Um pendulo é formado prendendo-se uma haste longa e fina de complrimento e massa em um dado ponto, que está a uma distância acima do centro da haste. Encontre a equação diferencial do movimento e o período do pêndulo.
Passo 1
Primeiro vamos ver um esquema do pendulo descrito no enunciado:
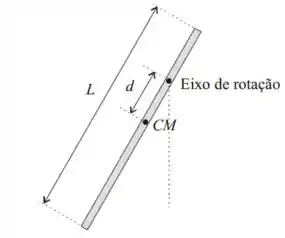
Assim, vamos equacionar esse problema.
Passo 2
Vamos usar a Segunda Lei de Newton para rotação:
Onde é o torque resultante, é o momento de inércia e é a aceleração angular.
Vamos calcular o torque em relação ao ponto do eixo, ou seja, o ponto que não se move:
Passo 3
Igualando as duas equações abaixo temos:
Como
Para pequenos valores de :
Então:
Passo 4
Assim, encontramos a equação do pêndulo. Mas calma essa equação é um MHS, né?
Vamos lembrar que no MHS podemos escrever:
Comparando as equações chegamos a:
Assim, o período de rotação é:
Resposta
Exercício Resolvido #5
UNA - Mecânica Aplicada - Vibrações Mecânicas
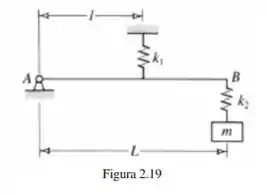
O sistema mostrado na Fig modela o braço de um mecanismo de elevação de peso. Determinar sua frequência natural de oscilação em torno do ponto .
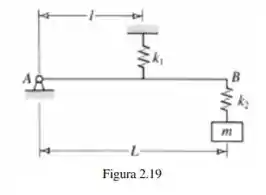
Passo 1
Primeiro vamos começar o problema, entendendo o que estamos buscando no problema e como vamos chegar à solução. Ok?
Pois bem, estamos buscando a frequência natural do - Movimento harmônico simples, mas que não é tão simples assim, não é mesmo rsrsrs. De acordo com a Teoria, se chegarmos a uma modelagem envolvendo uma EDO de 2º ordem como essa genérica aqui:
Então a frequência natural pode ser encontrada a partir do termo que multiplica . Então, basicamente devemos modelar o nosso problema e ver se a gente encontra algo parecido. Vamos nessa?
Passo 2
Para modelar o nosso problema, vamos basicamente utilizar em a física envolvida no nosso sistema: As Leis de Newton!
Considere então, o diagrama de forças livres no desenho a seguir:
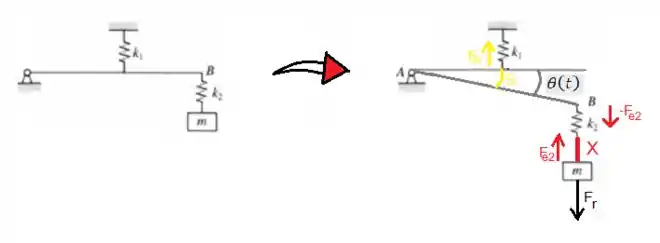
Na massa , temos basicamente a ação de duas forças: uma peso e outra proveniente da mola . Como a massa vibra, ela tem aceleração, logo tem força resultante. De acordo com as leis de Newton, a força resultante é a soma das duas únicas forças que atuam na mola:
Com isso temos a primeira equação. Agora, quero que você observe, também, que no problema, estamos trabalhando com rotações, então, também temos que encontrar uma equação para os torques!
Passo 3
As forças que causam torque na barra durante um tempo qualquer, é a resultante entre os torques causados pela mola 1 e pela mola 2 (duas únicas forças atuando sobre a barra):
Assim como a questão da força, devido ao fato da barra vibrar, tem aceleração, logo não podemos falar que a resultante é zero, saca?
Pronto, do sistema físico a gente tira duas equações:
Passo 4
Vamos estudar primeiro a primeira equação :
A força resultante é Newton mesmo: . A aceleração tem um detalhe importante que precisamos discutir: ela é a aceleração resultante da massa:
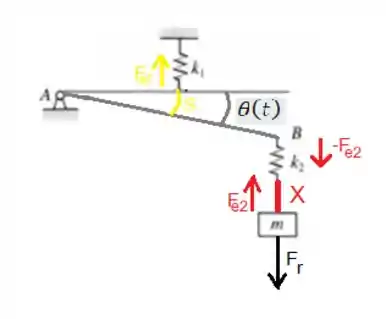
No caso, a massa têm dois deslocamentos: em vermelho e em verde. Como sabemos a aceleração resultante será a segunda derivada do deslocamento total em relação ao tempo:
O arco é dado pelo produto do raio pelo ângulo do arco:
Então...
Show! Agora vamos falar da força elástica : como qualquer força elástica...
A força peso, no entanto:
Então a gente conclui isso aqui:
Passo 5
Vamos estudar primeiro a segunda equação :
Novamente, vamos começar pela resultante: . Como estamos trabalhando com um sistema sem perdas de energia (característica de um MHS), podemos falar que o torque resultante em qualquer tempo, é o mesmo torque do início do movimento:
O legal de olhar o início, é que como as molas não estão esticadas, a única força que faz torque é o peso, então o torque resultante é:
O torque da mola , é o produto da força elástica pela distância de aplicação:
Lembrando que , onde é o arco amarelo de distorção da mola , dado pelo raio vezes o ângulo de distorção...
O torque da mola , por outro lado:
Esse menos é porque a força da mola que influencia no torque da barra é essa daqui:

Mas é a mesma coisa do passo anterior...
Então... Concluímos esse com:
Passo 6
Com os dois passos anteriores, nos chegamos nessas duas equações:
Vamos pegar essa segunda equação, isolar o (ou o porque tanto faz kkk):
Para substituir isso na primeira equação, vamos precisar da segunda derivada:
O primeiro termo dessa derivada é constante, logo sua deriva é ...
Calculando agora a segunda derivada...
Substituindo e na equação ...
Simplificando ainda mais...
Dividindo todo mundo que multiplica o para chegar à equação que a gente quer chegar...
Passo 7
Prontinho! Comparando então a EDO que acabamos de encontrar com a EDO geral de segunda ordem:
Concluímos que a frequência fundamental é:
Ou ainda: