Funções de Duas Variáveis
Produzido por Bruno NeresTeoria
Fala aí galerinha, nós somos o Responde Aí, a plataforma de exatas criada para levar até você um ensino de qualidade e bem didático.
Nosso papo hoje é sobre as funções de duas variáveis, então, bora lá!
Funções de Duas Variáveis
As funções de duas variáveis nada mais são que expressões matemáticas que pegam duas variáveis,
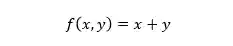
Para cada par de valores

Assim como para as funções de uma única variável é importante sabermos o domínio e a imagem, para as funções de duas variáveis também precisamos conhecer quem são esses dois conjuntos.
Domínio
O domínio é definido como a região na qual as variáveis independentes estão definidas.
Para uma função de uma variável,
Agora, para as funções de duas variáveis, o domínio será uma região no plano
Tá, beleza, o domínio vai ser uma região no plano, mas como olhar para uma função de duas variáveis e encontrar o domínio dela?
Para isso, nós temos que olhar para a função e garantir os seguintes pontos:
- Nas frações o denominador NÃO PODE SER ZERO;
- Dento de raiz quadrada NÃO pode ter número negativo;
- O valor dentro do logaritmo tem que ser SEMPRE POSITIVO.
Vamos pegar um exemplo pra ficar mais claro:
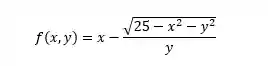
Primeiro você deve ser perguntar: Tem fração na expressão da função?
Para esse caso a resposta é sim, então temos que garantir que o denominador, que nesse caso é igual a
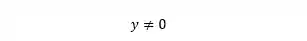
Agora, nos fazemos a segunda pergunta: Tem raiz quadrada na expressão?
Novamente a resposta é sim, então temos que garantir que a expressão que está dentro da raiz, que nesse caso é
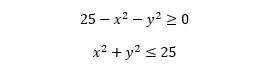
E agora temos que nos fazer a última pergunta: Tem logaritmo na expressão?
Nesse caso a resposta é não, então não precisamos garantir mais nada.
Nesse modo, o domínio desse função será todos os pares de valores
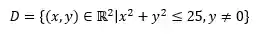
Imagem
A definição de imagem é bem simples, basicamente é o conjunto de todos os valores que uma função assume.
No domínio nós tínhamos o junto de todos os valores que o par
Devemos ficar atentos as seguintes coisas:
- Raízes quadradas: as raízes quadradas sempre nos retornaram um número positivo;
- Termos ao quadrado: os termos ao quadrado também sempre nos retornaram um número positivo
Vamos lá pra um exemplo para ficar mais claro:
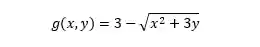
Primeira pergunta: Tem raiz?
Tem, então sabemos que essa raiz nos retornará um número positivo, logo:
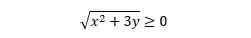
Podemos fazer algumas manipulações para encontrarmos a expressão da função, desse jeito aqui:
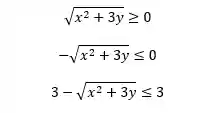
E assim temos que a expressão da nossa função sempre será menor ou igual a 3.
Então, a imagem,
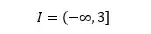
Tranquilo, não é?
É isso que temos para falar hoje sobre funções de duas variáveis.
Além de conteúdo irados em textos, nós do Responde Aí também temos exercícios resolvidos passo a passo em texto e em vídeos. 🎉
Eu vou deixar aqui embaixo um vídeo, no qual a gente resolve um exercício sobre funções de duas variáveis passo a passo com você. É ótimo para praticar. Confere aí 👇🏽
Curtiu nosso conteúdo? Então assine com a gente para ter acesso a muito mais!
Exercícios Resolvidos
Exercício Resolvido #1
CEFET-RJ, P1 prof. Roberto Thomé, exercício 2
Determine e esboce o domínio de
Passo 1
Essa é tranquila! O comando está bem claro, então é só colocar os nossos passos em ação!
Vendo a nossa função com atenção, podemos destacar dois casos que interferem no domínio:
1-Dentro das raízes de índice par não pode ter número menor que
2-O denominador da fração não pode ser
Agora podemos estabelecer as restrições da função!
Passo 2
A primeira restrição é dentro das raízes pares não pode ter número menor que .
Então, vamos analisar o termo,
Para que dentro da raiz seja maior ou igual a zero, temos que
Também temos na função outra raíz par,
Para que dentro da raiz seja maior ou igual a zero, temos que
Por último, também temos um termo que é uma raiz impar,
Como é uma raíz ímpar, não temos restrição nenhuma!
Passo 3
A segunda restrição é que o denominador da fração não pode ser
Então vamos analisar o termo que é uma fração
Para que o denominador não seja zero, temos que
Logo,
Agora, unindo as duas restrições para este termo, temos que , o argumento da raíz, não pode ser menor que ! Então vamos atualizar o resultado que encontramos no Passo 2.
Então a restrição fica assim,
Passo 4
Então agora chegamos em duas condições para se avaliar. A primeira é,
E como que você descobre o que essa desigualdade representa no plano? Basta fingir que é uma igualdade!
Veja, ficaria assim:
Essa é a reta que aponta pra baixo, passando pelo segundo e quarto quadrantes! Agora é só colocar o sinal da desigualdade de novo!
Ou seja, essa parte do domínio é tudo à direita da reta , excluindo a reta (porque o sinal é só de “maior que”, e nao de “maior ou igual”). Enfim, encontramos isso:
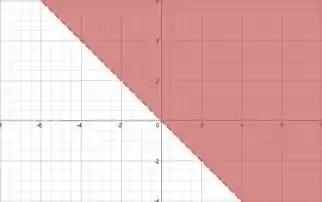
A outra condição é
temos algo parecido. Agora teremos a reta , e como o sinal é de maior ou igual, a reta está inclusa, é pegamos tudo à sua direita. Fica assim:
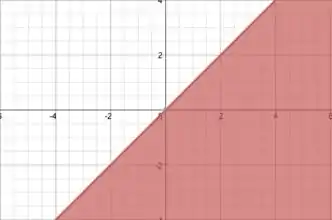
Passo 5
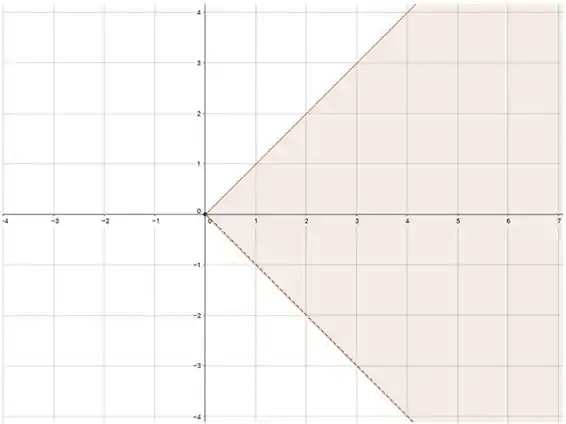
Pra gente esboçar o domínio todo é só sobrepor os que já temos! Fica assim:

Resposta
O domínio é dado por que é a interseção do gráfico acima
E seu esboço é:
Exercício Resolvido #2
Elaboração Própria
Encontre o domínio da função
Passo 1
Temos uma questão que pede pra gente descobrir onde a função existe (ou seja, qual é o seu domínio). Mas, convenhamos... é muito mais fácil descobrir onde ela não existe!!
Nossa função é uma fração, então a primeira coisa que devemos bater o olho é no denominador: ele não pode valer 0.
Vamos ver como é o gráfico da função logaritmo:
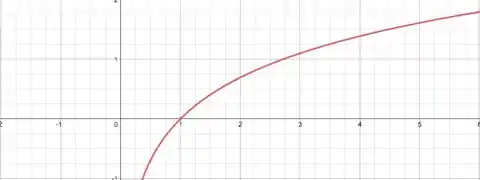
Olha só! Quando seu argumento é , seu valor é (é o ponto onde ela corta o eixo x). Portanto, como o valor do denominador da função do enunciado não pode valer ,
Igualando um argumento ao outro...
Passo 2
Ainda olhando para o gráfico da função logaritmo, observe que ela não está definida em ou números menores que 0. Ou seja, o argumento da função logaritmo só podem ser números maiores do que :
Passo 3
Pronto, agora que todos os problemas do denominador foram devidamente resolvidos, podemos olhar pra parte de cima da fração
Veja, temos aqui uma raíz quadrada
E seu interior não poder valer menos do que
Assim, fica:
Passo 4
Agora é só juntar tudo!
Do passo temos que
Do passo 2 temos que
E, do passo 3, temos que
Assim, nosso domínio é definido por:
Se não se sentir à vontade com a notação matemática (como eu... rsrs), é só escrever por extenso mesmo na prova! Isso aí em cima, lendo em português, diz que o domínio da função é o conjunto dos pontos , sendo e pertencendo aos reais, tais que e
Resposta
Exercício Resolvido #3
Elaboração própria
Determine a imagem de nos seguintes casos:
a)
b)
c)
d)
Passo 1
É bom adquirir o reflexo de achar o domínio da função antes de partir pra imagem. Então vou fazer isso sempre, beleza?
a)
Primeiro podemos notar que não há nenhuma restrição na função, portanto seu domínio é todo o . Enfim, temos:
Portanto, a imagem de é o conjunto . Tranquilo né? Vamos pra próxima!
Passo 2
b)
Nessa função tem uma restrição, por causa do logaritmo:
Mas bom, isso não vai afetar a nossa imagem. Isso porque o logaritmo, ao contrário da exponencial, pode assumir valores negativos, positivos, todos os valores do !
Assim,
Ou seja, a imagem de é todo o !
Passo 3
c)
Mano, essa não tem muito mistério. É só uma função polinomial meio aleatória e sem nenhuma restrição (seu domínio é todo o ).
Nesse caso, não tem muito como justificar, mas intuitivamente podemos dizer que essa função pode assumir qualquer valor, e que, portanto, sua imagem é todo o .
Passo 4
d)
Opa, essa aqui já é mais interessante!
A única restrição nessa função é a raiz quadrada, então temos:
Então o domínio da função é o conjunto dos do que respeitem essa condição.
Passo 5
Agora repare que:
Uma vez que a função exponencial é sempre crescente, podemos aplicar essa função dos dois lados da inequação:
Por isso que é importante saber o domínio da função!! O valor máximo que esse termo pode assumir é 1, por causa da restrição da raiz quadrada.
Raiz quadrada, que é, aliás, positiva:
Então temos
Assim, a imagem de é o conjunto .
Resposta
a)
b)
c)
d)
Exercício Resolvido #4
Elaboração própria
Esboce o gráfico da função
Passo 1
Identificar a superfície:
Fazer :
Essa é a equação da esfera!
Passo 2
Mas como
Devemos ter . Portanto, é apenas a parte superior da esfera.
Além disso, como estão elevados ao quadrado serão sempre positivos. Com aquele sinal de menos ali na frente eles vão sempre ser quantidades que vão subtrair! Portanto, o máximo ocorre onde . Ou seja, :
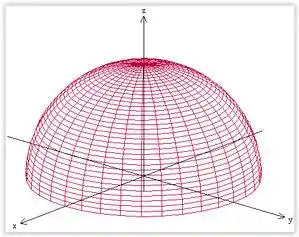
Resposta
Exercício Resolvido #5
UERJ, Lista 3 prof. Hamilton, exercício 6e
Esboce o gráfico da função
Passo 1
Então o enunciado me deu uma função de duas variáveis , a gente pode plotar as raizes dessa equação em um terceiro eixo . Ou seja, vamos colocar nossa variável para acharmos mais facilmente o desenho dela. Chamamos então,
Agora vamos avaliar alguns planos!
Passo 2
Vale perceber que nossa função é , mas na real o não aparece nela!! Isso é um indicativo que ela tem o mesmo perfil ao longo do eixo .
Então vamos ver a curva dela no plano , anulando a variável , já que nossa função nao depende dela, lembra?
Temos uma equação de elipse que se estende por todo eixo !! Ou melhor, temos apenas a parte de cima de uma elipse, já que estamos pegando apenas e não !
Passo 3
A gente acabou de fazer o plano , mas como ficaria o plano . Para isso precisamos fazer
Olha!! Uma reta! Muito simples, na verdade... é uma reta no plano , que fica constantemente em altura ! Ele será um máximo na superfície.
Passo 4
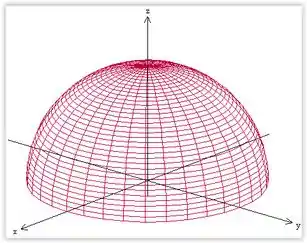
Galera, no Passo , a gente viu que é a metade de uma elipse que se estende por todo eixo . No Passo 3, vimos que essa curva atinge um valor máximo em
Jogando isso pro gráfico, ficamos com,
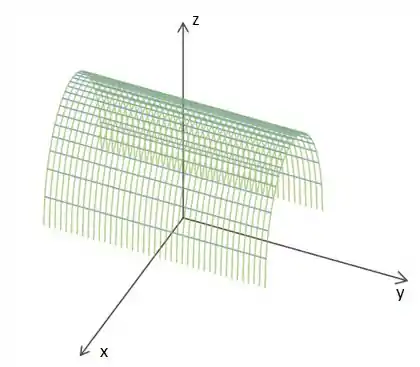
Resposta
A resposta é só repetir o gráfico acima!
Exercício Resolvido #6
UERJ, Lista 1 prof. Renata, exercício 2d
Esboce o gráfico da função
Passo 1
Temos uma função de variáveis, então vamos escrevê-la na forma
Essa é a equação da superfície que temos que esboçar.
Prestando atenção, podemos ver que ser trata da equação de um paraboloide. Dá até pra reparar que ele é voltado pra cima, porque os coeficientes multiplicando e são positivos.
Vamos ver isso com calma analisando as interseções do gráfico com os planos coordenados :)
Passo 2
Então vamos anular as variáveis, uma por uma.
Começando pela variável por exemplo, podemos ver como é a interseção da superfície com o plano . Fazendo :
Opa! Uma equação de uma parábola, bem tranquila! Saca só:
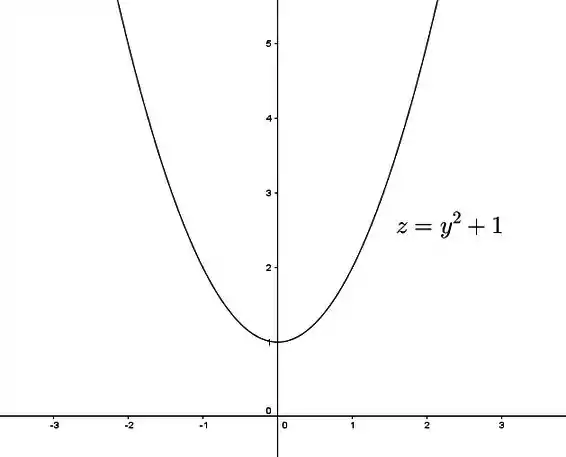
Passo 3
Agora vamos zerar a variável ! Assim, no plano vamos ter:
que também é uma parábola tranquila de esboçar. Ela vai ser bem parecida com a outra, mas por causa desse ela vai ser mais “pontuda”:
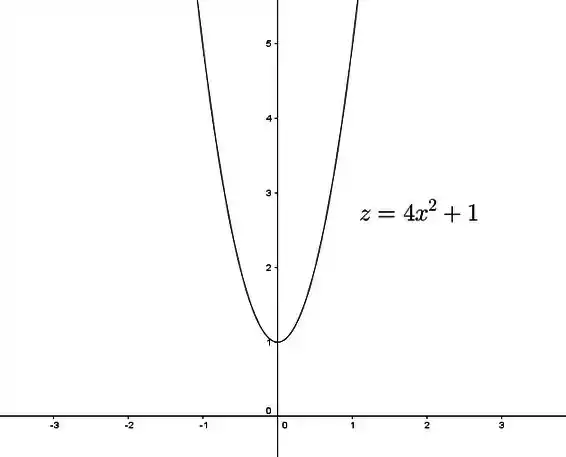
Passo 4
Agora só falta zerar a variável !
Fazendo, portanto, , obtemos:
Repare que essa equação não tem solução!!
Temos
Ou seja, a nossa superfície fica acima do plano !
Passo 5
Resumindo, o nosso gráfico é um paraboloide elíptico voltado pra cima, com vértice no ponto . Ele é mais largo no plano e mais magrinho no plano .
Agora, tendo em mente tudo isso que vimos, eu só te digo uma coisa: partiu esboçar essa bagaça!!
O gráfico ficaria assim:
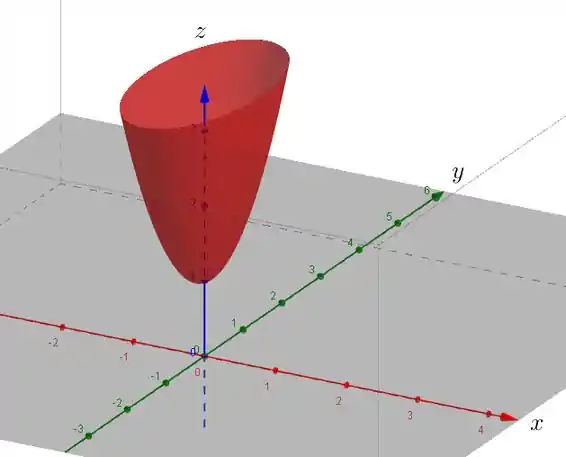
Resposta
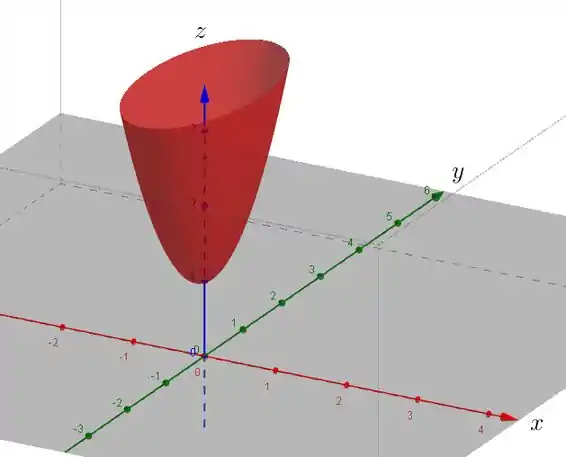
Exercício Resolvido #7
UFF, P1 2013.2 Cálculo IIB prof. Sérgio, exercício 2
Considere a função
- Esboce o domínio de .
- Esboce o gráfico de determinando sua interseção com os eixos coordenados.
Passo 1
a)
Para achar o domínio temos que lembrar que o termo dentro da raiz quadrada não pode ser negativo! Com isso,
Opaa, peraí! Isso tá com cara de elipse!
De fato, temos que
é a equação de uma elipse centrada na origem e com semieixos valendo e .
Como temos uma sinal de , temos que o domínio da é tudo que está fora da elipse (ou seja, tudo que é maior ou igual a 1). Em outras palavras, será o , menos a região dentro dela.
O esboço do domínio vai ser (só vale a parte rosinha):
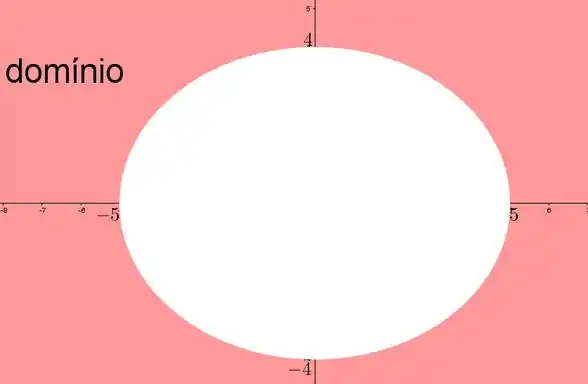
Passo 2
b)
Agora ele pediu o esboço do gráfico. Mas antes de resolver seguindo o enunciado, eu vou dar um bizu aqui!
Nosso reflexo tem que ser: chamar de ! Assim vamos ter:
Podemos elevar ao quadrado (mas tem que tomar muito cuidado com isso, vou explicar o porquê depois):
Galerinha, para quem não lembra, nós temos aqui a equação de um hiperboloide de uma folha, com eixo em . É aquele cara com forma de reator de usina nuclear:
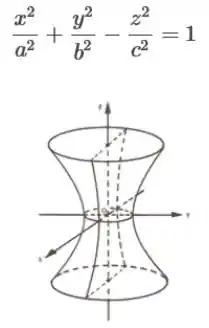
Então fica a dica, sempre bom estar com o gráfico de algumas equações na memória, pois pode ajudar muito a resolver algumas questões!
Passo 3
Mas atenção!! Até separei um passo pra isso porque é bem importante!
A nossa função de origem é
Ou seja, . Enquanto que na equação que achamos depois, do hiperboloide, admite valores negativos! Mas, repito, na nossa função não podemos ter valores negativos de .
Portanto, o nosso gráfico vai ser na verdade só metade desse hiperboloide, só a parte acima do plano !
Beleza?? Tem que ficar esperto com isso!
Passo 4
Enfim, continuando e resolvendo de acordo com o enunciado! Nós temos que seguir o procedimento padrão: analisar as interseções do gráfico com os eixos coordenados.
Vamos começar zerando a variável . Assim, podemos obter a interseção do nosso gráfico com o plano :
que é exatamente a equação da elipse que delimita o domínio da função, e que já vimos na letra a):
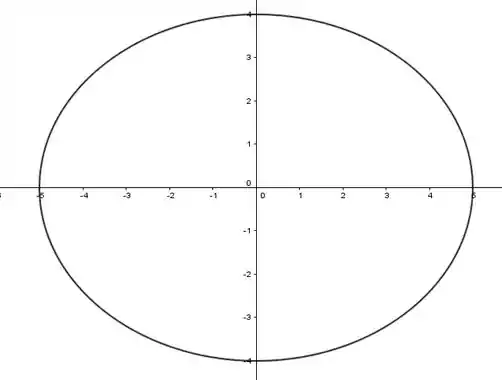
Beleza, vamos prosseguir!
Passo 5
Agora vamos zerar a variável . Vamos ter:
Opa, é agora que o nosso gráfico começa a justificar seu nome de hiperboloide! Pois isso nada mais é que a equação de uma hipérbole.
O seu esboço ficaria assim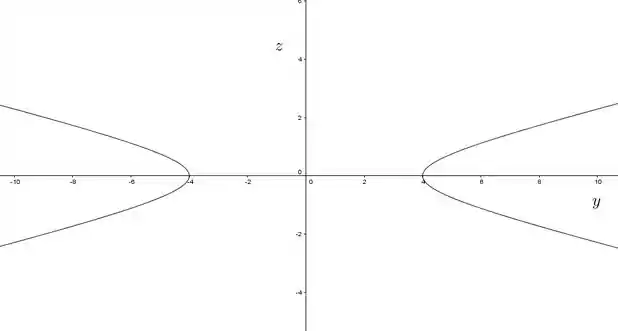
Lembrando que pro nosso gráfico só vamos considerar a parte com !!
Passo 6
Agora só falta zerar o pra ver o que tá rolando no plano :
Novamente temos uma hipérbole, que vai ser um pouco mais “pontuda” que a anterior por conta desse no lugar do :
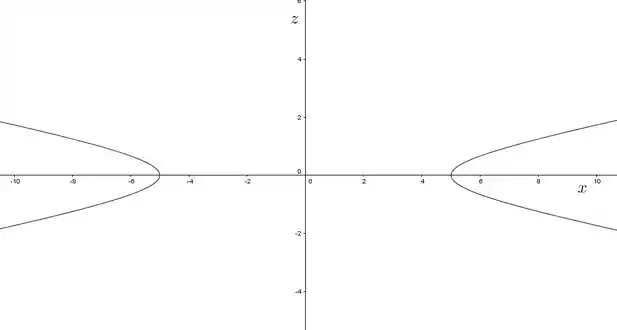
Vou repetir de novo, sou chato mesmo: pro gráfico a gente só vai usar a parte com positivo!
Passo 7
Bem agora não tem jeito, é mão na massa! A partir de isso tudo que a gente viu, com determinação deve dar pra tirar um esboço decente do gráfico! Quero ver sangue no olho, que esse gráfico é chatinho de desenhar mesmo!!
Enfim, daria alguma coisa mais ou menos assim:
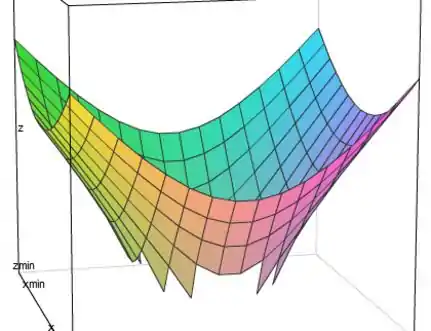
Viu, até no computador é chato de desenhar ;)
Resposta