Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Curvas De Nível

Ver Todos os Exercícios

Teoria

Fala aí! Hoje vamos aprender um pouquinho melhor sobre curvas de nível, e como o cálculo vai nos ajudar a representar funções de várias variáveis!

Vem comigo 😆

⭐ Veja também ⭐

O que são curvas de nível?

Em Cálculo, curvas de nível são ferramentas usadas para visualizar funções de várias variáveis representadas em dimensões inferiores.

Basicamente, a gente quer encontrar um jeito simples de desenhar uma função tridimensional (ou às vezes de ordem maior ainda) em um papel, que é só bidimensional. É a mesma ideia daqueles mapas topográficos que a gente vê em Geografia, sabe?

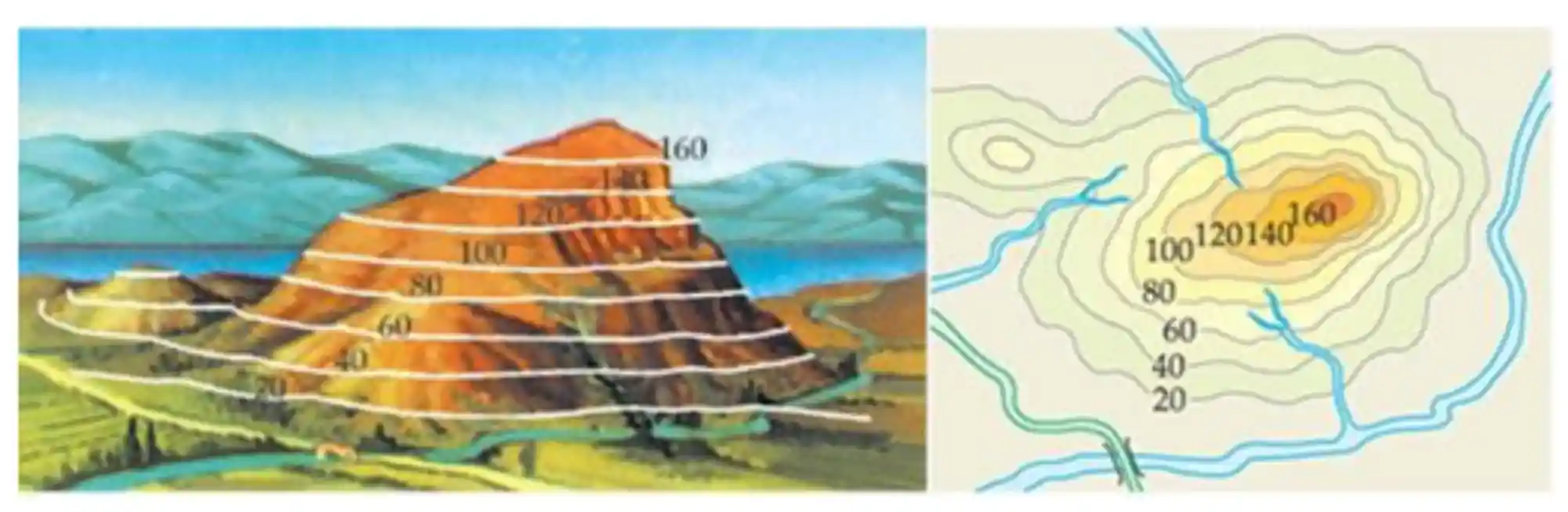
Representação do mapa topográfico de uma montanha.
Representação do mapa topográfico de uma montanha.

Como fazer o cálculo de curvas de nível

Para calcular uma curva de nível de uma função , é só a gente igualar .

A definição formal é a seguinte:

Seja um número real. Uma curva de nível de uma função é o conjunto de todos os pontos pertencentes ao domínio de , tais que .

Falando assim parece complicado, né? Mas prometo que já vai ficar mais claro!

Olha só, quando a gente olha pro gráfico da função , a gente vai ver o seguinte:

Gráfico da função
Gráfico da função

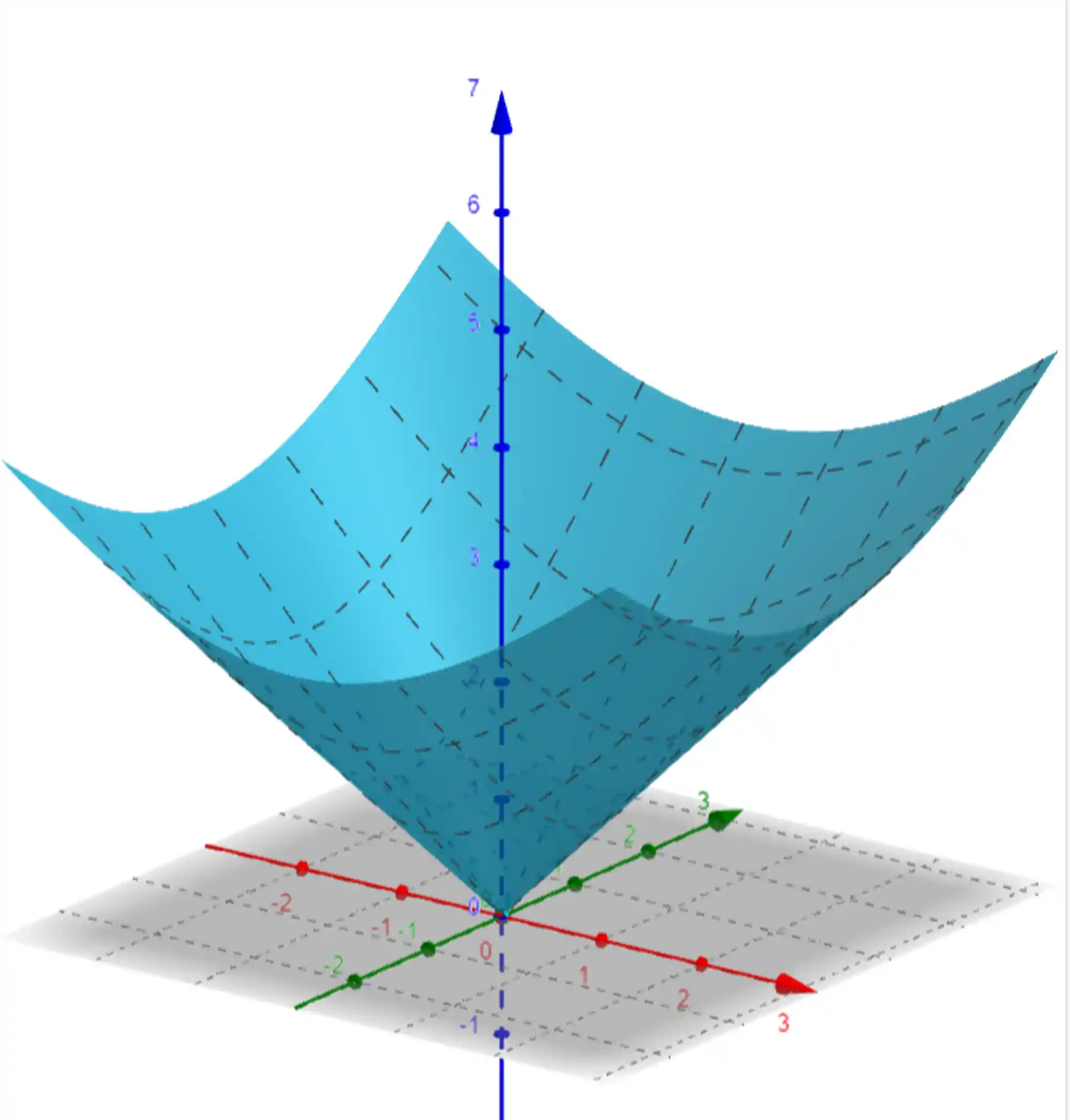
Agora, vamos olhar para aquela definição ali em cima e tentar imaginar o que seria a curva de nível 1 dessa função. 🧐

De acordo com a definição, a curva de nível 1, , seria o conjunto de todos os pontos do domínio de para os quais .

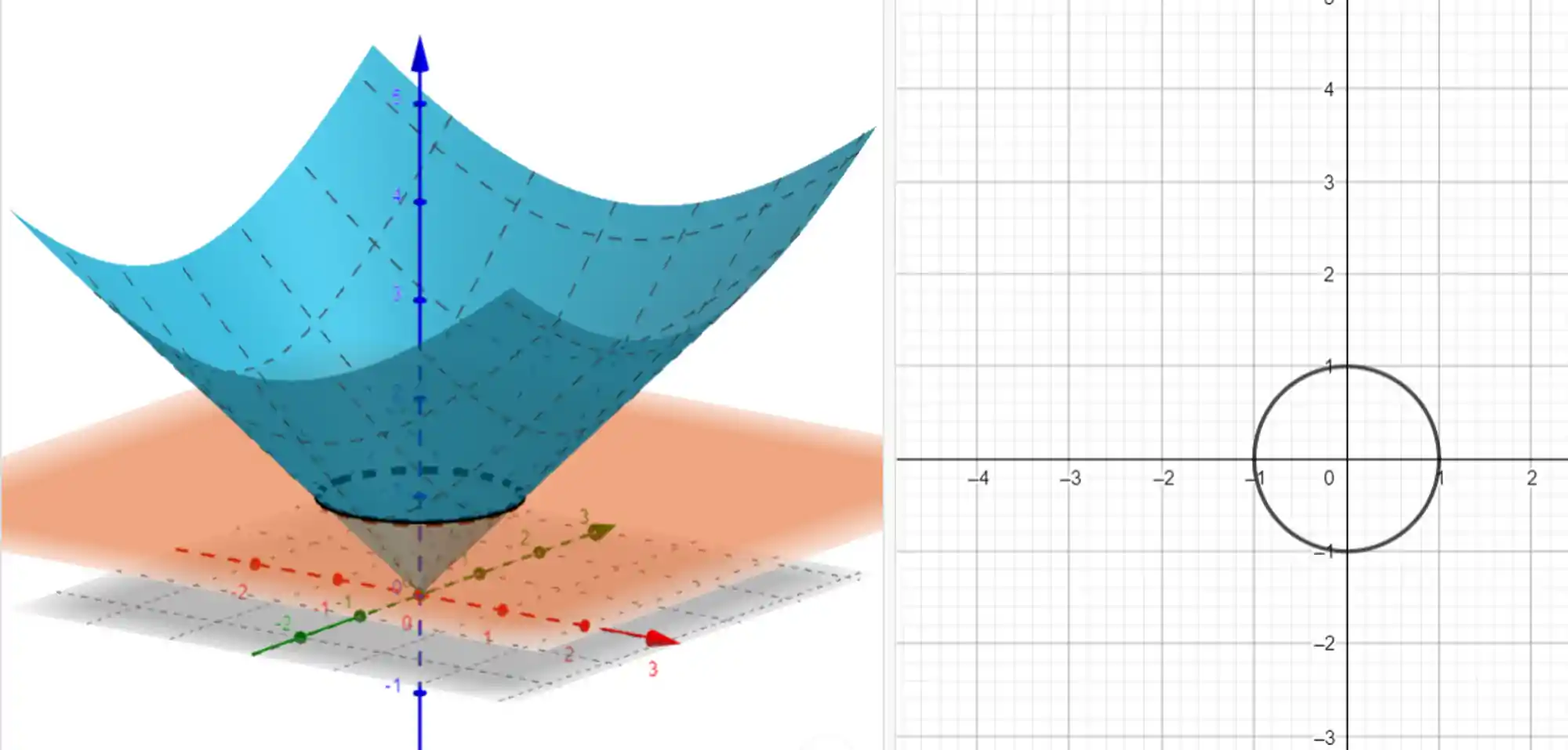
Olha só, vendo esse gráfico aí em cima de lado, o tá naquela linha fininha que aparece ali:

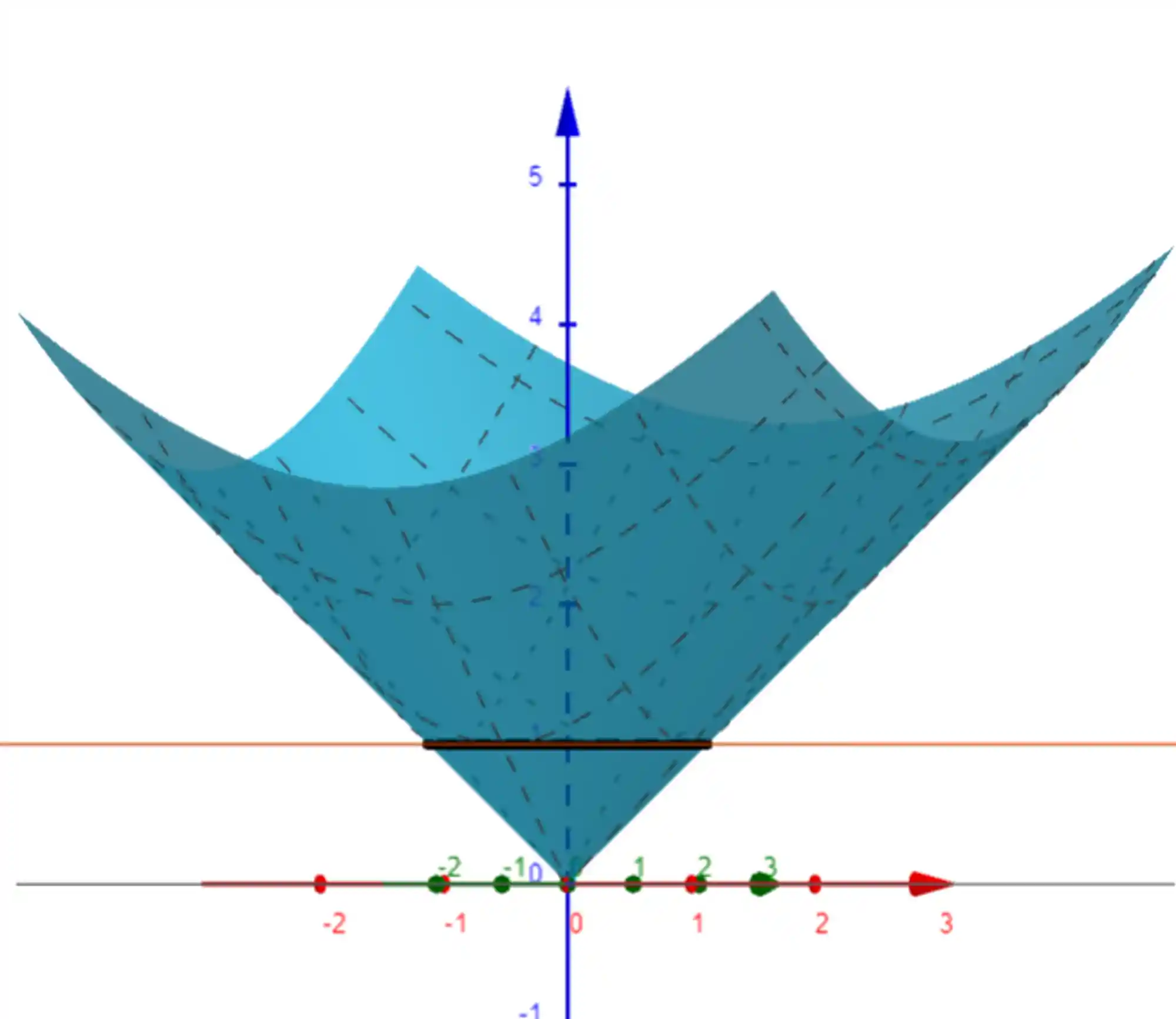
Gráfico de
Gráfico de

Então, a curva de nível 1 vai ser o conjunto de todos os pontos em que esse plano intercepta o gráfico da nossa função!

Vou marcar essa interseção com um círculo preto ali no gráfico abaixo, ó:

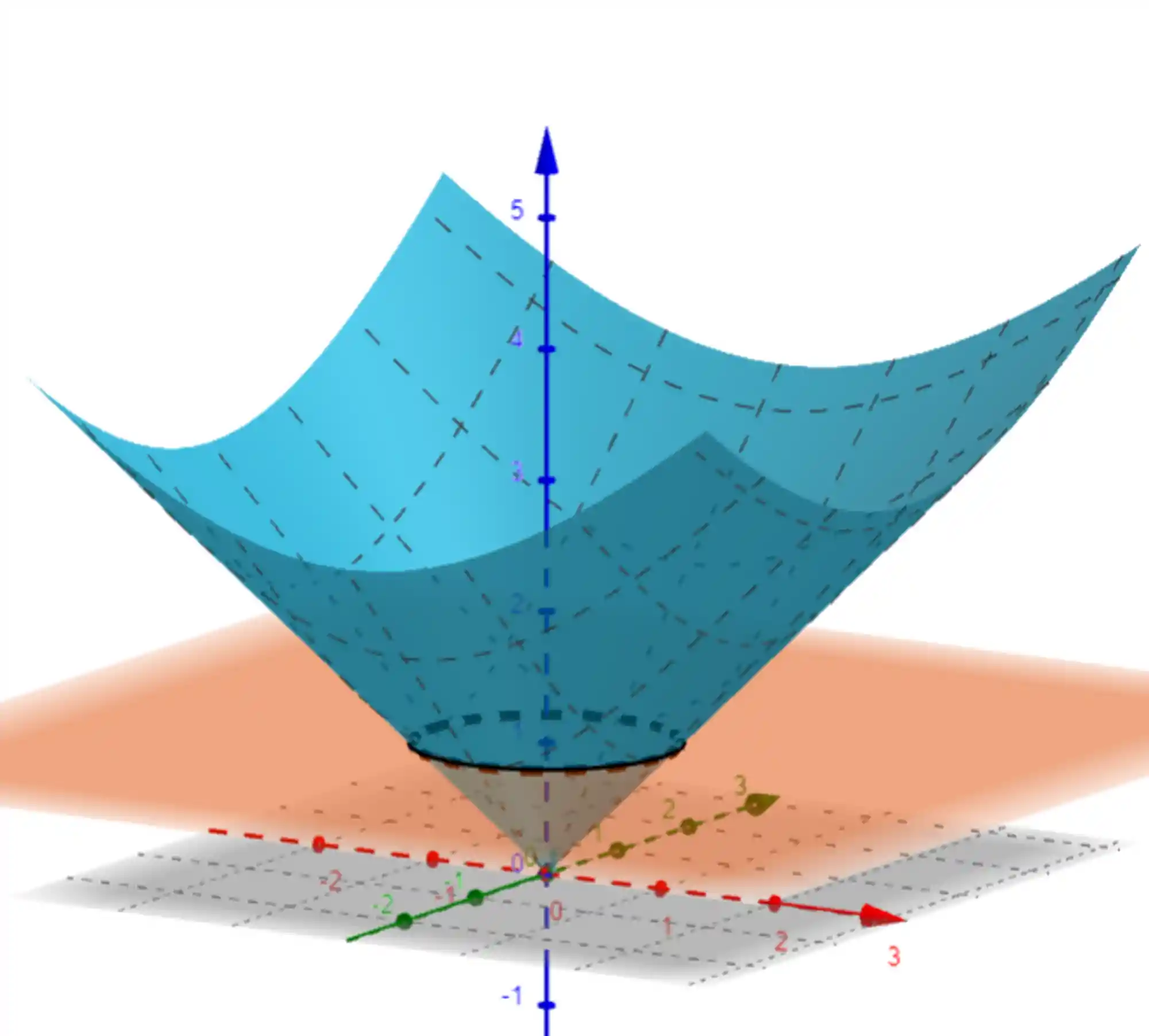
Curva de nível 1 evidenciada.
Curva de nível 1 evidenciada.

Aí, repara só numa coisa: como a gente viu nesses gráficos ai, a curva de nível de uma função pertence tanto ao gráfico de quanto ao plano . Então, para acharmos a equação dessa curva de nível , é só igualarmos a função a essa constante!

Vamos achar a equação da curva de nível que a gente tava estudando anteriormente. É só igualar a função a 1:

Essa é a curva de nível da nossa função no nível . E sua equação é a de uma circunferência de raio 1 com centro na origem!

Gráficos de
Gráficos de

Se ficou perdido em algum momento, assiste esse vídeo rapidinho aqui que te explico de um jeito bem diretinho 👇

Mapa de Contorno

Mapa de contorno é o nome dado à representação das curvas de nível de uma função em .

O negócio aqui é desenhar várias curvas de nível para uma função , até que a gente tenha uma noção boa do comportamento do gráfico da própria função mesmo.

Imagina o seguinte, quando você olha para aquele exemplo da montanha lá, se tivesse só uma curva de nível no mapa topográfico, não daria pra ter nenhuma ideia que na realidade existe uma montanha ali, concorda? Mas conforme você vai adicionando mais curvas de níveis diferentes, vai obtendo valores maiores, e aí já dá pra começar a ter uma ideia que esse relevo tá crescendo pra formar uma montanha!

Pegou a ideia? Porque é exatamente a mesma coisa que vamos fazer aqui!

Vamos aplicar isso aí no seguinte exemplo 👇

Exemplo: Desenhe o mapa de contorno da função .

A gente já viu que é só igualar a expressão da função a uma constante , né? Então vamos fazer isso, deixando como uma constante genérica mesmo:

A partir dessa equação, vamos analisar os intervalos de para ver que tipos de curvas de nível a gente tem.

Repara que, se o termo for positivo, a gente tem a equação de uma circunferência. Pois a soma de dois termos quadráticos positivos igual a um outro termo positivo fornece a equação de uma circunferência.

Então, se

nossas curvas de nível são circunferências de raio .

E se ? Bora substituir na equação e descobrir:

Repara que essa igualdade só é satisfeita quando e . Então, nossa curva de nível em , na verdade é o ponto .

Só falta ver o caso com . Bora lá:

Se , o lado direito da equação fica negativo. Como o lado esquerdo é sempre positivo (já que as variáveis tão elevadas ao quadrado), essa equação não tem solução. Então, não temos curvas de nível para 😔

Vamos resumir o que a gente achou:

  • Não há curvas de nível.
  • Só temos o ponto .
  • As curvas de nível são circunferências centradas na origem de raio igual a .

Então, só pra ficar mais bonitinho o nosso gráfico: se , a circunferência vai ter raio igual a 1; se , a circunferência tem raio igual a e assim por diante.

Olha como fica nosso resultado:

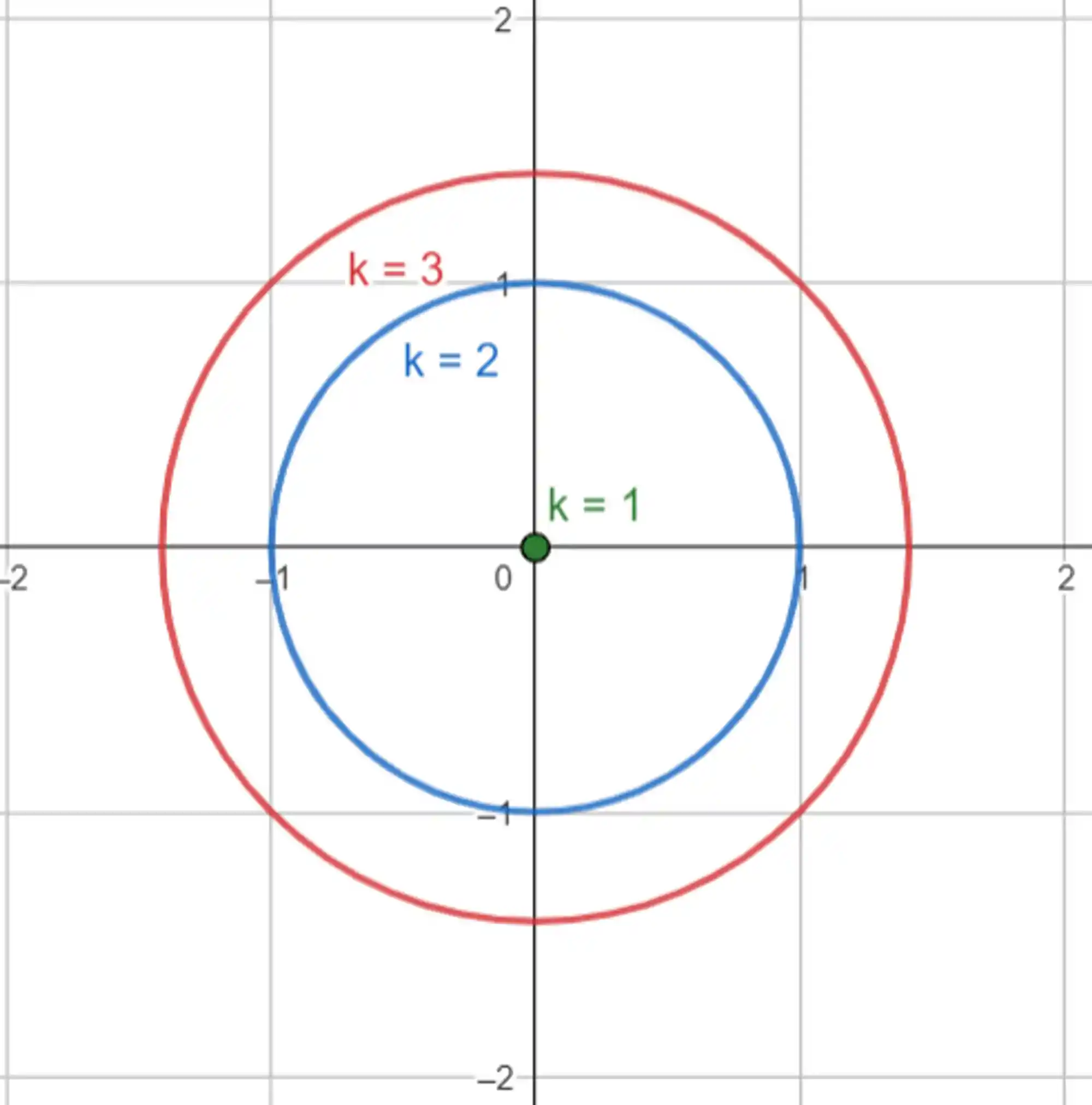
Mapa de contorno para
Mapa de contorno para

Beleza? É muito importante não esquecer daquele pontinho ali na origem, porque pro mapa de contorno, a gente sempre tem que desenhar todos os tipos de curvas de nível.

Bora praticar com mais alguns exercícios!

Mapa de Contorno

Exemplo: Desenhe o mapa de contorno da função .

Exercícios Resolvidos

Exercício Resolvido #1

James Stewart, Cálculo – Volume 2, 6ª ed. São Paulo: Cengage Learning, 2010, p. 827 - 41

Faça o mapa de contorno da função mostrando várias curvas de nível.

f x , y = y - ln ⁡ x

Passo 1

Essa é tranquila! Pra achar as equações das curvas de nível, basta igualar a função a uma constante qualquer k :

y - ln ⁡ x = k

⇒ y = ln ⁡ x + k

Ou seja, só precisamos esboçar vários gráficos dessa forma, fazendo variar o k .

Passo 2

Quando acrescentamos uma constante numa função, deslocamos seu gráfico na vertical. Dá uma olhada:

Na figura temos, de verde, o gráfico da função y = cos ⁡ x e em cima, de laranja, o gráfico da função y = cos ⁡ x + 2 .

E basicamente nessa questão vamos ter que fazer a mesma coisa, mas com a função y = ln ⁡ x , deslocando o gráfico pra cima e pra baixo dependendo do valor de k !

Passo 3

O gráfico da função y = ln ⁡ x   é assim, lembra?

Agora vamos fazer um estudo para vários intervalos de k :

k > 0

k = 0

k < 0

Quando temos k = 0 , a função não irá se deslocar nem para cima, nem para baixo, ficando igual ao gráfico acima.

Passo 4

Agora vamos analisar a função para, k > 0

Neste caso a função será deslocada para cima, dependendo do valor de k .

Passo 5

Agora vamos analisar a função para, k < 0

Neste caso a função será deslocada para baixo, dependendo do valor de k .

Passo 6

Para exemplificar, eu fiz k valer - 2 ,   - 1 ,   0 ,   1 e 2 , o que resultou nesse lindo arco-íris de curvas de nível:

Resposta

Exercício Resolvido #2

Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, p. 71 – exemplo 3.3

A temperatura em um ponto ( x , y ) de uma placa de metal plana é T x , y = 9 x 2 + 4 y 2 graus.

  1. Encontre a temperatura no ponto ( 1 ,   2 ) .
  2. Encontre a equação da curva ao longo da qual a temperatura tem um valor constante e igual a 36 graus.
  3. Esboce a curva do item (b).

Passo 1

Resolvendo o item (a):

Basta substituir x = 1 e y = 2 para descobrir T ( 1,2 ) :

T x , y = 9 x 2 + 4 y 2

T 1,2 = 9 1 2 + 4 2 2

T 1,2 = 9 + 16

⇒ T 1,2 = 25

Passo 2

Resolvendo o item (b):

Queremos encontrar a curva em que a temperatura é constante e igual a 36 . Logo:

T x , y = 36

⇒ 9 x 2 + 4 y 2 = 36

Dividindo os dois lados por 36 :

9 x 2 36 + 4 y 2 36 = 36 36

⇒ x 2 4 + y 2 9 = 1

Portanto, os pontos ( x , y ) que satisfazem essa equação satisfazem T x , y = 36 .

Observação: note que esses pontos são uma curva de nível da função T ( x , y ) !

Passo 3

Perceba que equação da curva que acabamos de encontrar é uma elipse.

Portanto, seu gráfico é o seguinte:

Resposta

  1. T 1,2 = 25

  2. x 2 4 + y 2 9 = 1

Exercício Resolvido #3

Hamilton Luiz Guidorizzi, Um Curso de Cálculo – Volume 2, 5ª ed. Rio de Janeiro: LTC – Livros Técnicos e Científicos Editora S.A., 2001, p. 161 – 2c

Desenhe as curvas de nível e determine a imagem:

f x , y = x - y x + y

Passo 1

Antes de determinar as curvas de nível, é importante saber qual o domínio da função!

Repara que temos uma fração, então o denominador não pode zerar, ou seja,

x + y ≠ 0

Deste modo, temos que a função não é definida no ponto ( 0,0 ) , pois zeraríamos o denominador.

Vamos por partes! Pra achar as equações dessas curvas de nível temos que igualar a função a uma constante qualquer k :

x - y x + y = k

Vamos lá!

Passo 2

Vamos tentar isolar o y , deixando ele em função de x :

x - y = k x + y

⇒ k y + y = x - k x

y k + 1 = x 1 - k

y = 1 - k 1 + k x

Beleza, aí está nossa equação explícita! Agora vamos analisar possíveis valores de k .

Passo 3

Começando pelo caso mais simples: k = 0 . Isso dá simplesmente

y = 1 - 0 1 + 0 x ⇔ y = x ,

que é uma reta bem fácil de esboçar:

Repare que nossa função f ( x , y ) não está definida no ponto ( 0,0 ) , por isso tem essa bolinha aberta ai na origem, já que se a função não tá definida num ponto, a curva de nível não pode passar por esse ponto, beleza?

Passo 4

Outro caso bem tranquilo é a curva de nível k = 1 :

→ y = 1 - 1 1 + 1 x = 0 ,

que nada mais é que o eixo x :

Passo 5

Vamos fazer mais umas 2 curvas de nível que tá de bom tamanho. Vamos pegar um k > 1

Podemos usar agora k = 2 :

y = 1 - 2 1 + 2 x = - 1 3 x

Também sem grande mistério pra desenhar:

Passo 6

E agora, pra finalizar, que tal uma curva de nível com k   negativo?

Usemos então k = - 1 . Como não podemos zerar o denominador, vamos olhar a função de outra forma,

y = 1 - k 1 + k x →   ( 1 + k ) y = ( 1 - k ) x

Fazendo k = - 1 :

1 - 1 y = 1 + 1 x

x = 0

Tranquilho?!

O desenho é:

Passo 7

Juntando todas as curvas de nível que desenhamos:

Passo 8

Maas ainda não acabou a questão! Ele pediu também a imagem da função, lembra?

Relembrando, a imagem é o conjunto de todos os valores que a função pode assumir. E o fato da gente já ter olhado as curvas de nível da função vai ajudar bastante!

A função pode valer para vários valores de k :

f x , y = k

E o conjunto desses k que vai ser a imagem da função.

Então temos que descobrir quais valores de k são permitidos e quais não são. E na verdade já fizemos isso! Porque esse f x , y = k é a mesma coisa que a gente fez pra achar as curvas de nível, e acabou resultando na equação

y = 1 - k 1 + k x

Aí vimos que k pode valer qualquer coisa, inclusive - 1 .

Ou seja, a função pode assumir qualquer valor real, então sua imagem é o conjunto dos reais.

R

Resposta

Curvas de nível:

Imagem:

R

Exercício Resolvido #4

USP, P1 2011, exercício 1 (modificado)

Seja

f x , y = 2 x 2 + y 2 4 x - y 2

a) Esboce a curva de nível de f que corresponde ao nível z = 3 . Em que pontos essa curva intercepta o eixo x ?

Passo 1

a)

Ok, ele quer a curva de nível que tem z = 3 . Então, tudo o que temos que fazer é pegar a função f x , y e igualá-la a 3 :

2 x 2 + y 2 4 x - y 2 = 3

E agora partiu ver que curva é essa! Vamos desenvolver melhor essa equação?

2 x 2 + y 2 = 3 4 x - y 2

2 x 2 + y 2 = 12 x - 3 y 2

2 x 2 - 12 x + 4 y 2 = 0

Dividindo tudo por 2 ,

x 2 - 6 x + 2 y 2 = 0

Passo 2

Agora, o que acha de completarmos o quadrado para o x ? Só pensar que o coeficiente - 6 do x é duas vezes o coeficiente do x 2 vezes o segundo termo do produto notável. Assim,

x 2 - 6 x + 9 - 9 + 2 y 2 = 0

x - 3 2 + 2 y 2 = 9

x - 3 2 9 + 2 9 y 2 = 1

E pronto! Temos aí a equação de uma elipse, centrada em 3,0 !

Passo 3

Agora, analisemos o que o enunciado realmente pediu: em que ponto essa curva corta o eixo x ? Para saber disso, temos que fazer y = 0 , e então teremos o ponto pedido :)

x - 3 2 9 + 2 9 0 2 = 1

x - 3 2 = 9

Tirando a raiz quadrada dos dois lados,

x - 3 = ± 3

x = 0   o u   x = 6

Passo 4

Mas tome muito cuidado agora! Encontramos os pontos 0,0 e 6,0 , certo? Não! Temos apenas o segundo, pois a origem não faz parte do domínio da função! Isso porque substituindo os valores x , y = 0 ,   0 na função temos uma divisão por zero.

Assim, temos apenas o ponto 6,0 , pois a curva não toca a origem:

Passo 5

Coloquei direto a imagem da elipse, mas se você tiver alguma dúvida de como se esboça, é só lembrar da equação geral:

x - x 0 2 a 2 + y - y 0 2 b 2 = 1

Então, como nosso x 0 = 3 e y 0 = 0 , seu centro está em 3,0 . Aí para ver os semieixos, você pega, a partir do centro, + a e – a na direção x e + b e – b na direção y !

Resposta

a) Corta o eixo x no ponto 6,0 , apenas.

Exercício Resolvido #5

Elaboração própria

Considere a função

z = f x , y = ln ⁡ e x + y - 1

  1. Escreva a equação da curva de nível de f que contém o ponto 8,2 e da curva de nível que contém o ponto - 2,3
  2. Mais geralmente, escreva a equação da curva de nível de f que contém o ponto a , b , com b > - a .
  3. Mostre que o valor de f sobre a reta y = - x + 2 é constante, isto é, que y = - x + 2 está contida em um conjunto de nível de f .
  4. Mostre que o valor de f sobre a reta y = - x + 3 é constante, isto é, que y = - x + 3 está contida em um conjunto de nível de f .
  5. Se, por um momento, f representasse um lucro e você fosse um empresário, em qual reta você gostaria de estar: y = - x + 2 ou y = - x + 3 ? Justifique sua resposta.

Passo 1

a )

Para achar a curva de nível precisamos do valor de z , como ele deu um ponto que a curva de nível está vamos trocar esse ponto na função e achar nosso z , começando pelo ponto 8,2

z = f 8,2 = ln ⁡ e 8 + 2 - 1

z = ln ⁡ e 10 - 1

Para achar a curva de nível vamos fazer

ln ⁡ e 10 - 1 = f x , y

ln ⁡ e x + y - 1 = ln ⁡ e 10 - 1

Como temos logaritmos de mesma base podemos “tirar” o ln ⁡  

e x + y - 1 = e 10 - 1

e x + y = e 10

x + y = 10

E temos nossa curva de nível.

Passo 2

Vamos fazer a mesma coisa para o outro ponto - 2,3 ,

z = f - 2,3 = ln ⁡ e - 2 + 3 - 1

z = ln ⁡ e - 1

Para achar a curva de nível vamos fazer

ln ⁡ e - 1 = f x , y

ln ⁡ e x + y - 1 = ln ⁡ e - 1

Como temos logaritmos de mesma base podemos “tirar” o ln ⁡  

e x + y - 1 = e - 1

e x + y = e

x + y = 1

E temos nossa outra curva de nível.

Passo 3

b )

Vamos fazer a mesma coisa de novo, só que dessa vez no ponto a , b

z = f a , b = ln ⁡ e a + b - 1

z = ln ⁡ e a + b - 1

Para achar a curva de nível vamos fazer

ln ⁡ e a + b - 1 = f x , y

ln ⁡ e x + y - 1 = ln ⁡ e a + b - 1

Como temos logaritmos de mesma base podemos “tirar” o ln ⁡  

e x + y - 1 = e a + b - 1

e x + y = e a + b

x + y = a + b

E temos nossa curva de nível. Você deve estar se perguntando onde entra aquela restrição, isso serve para vermos que o cara dentro do ln ⁡   no valor de z é positivo, e assim podemos ter o logaritmo sem problemas. Ele é positivo porque

b > - a

b + a > 0

e b + a > e 0

e b + a > 1

e b + a - 1 > 0

Sacou?

Passo 4

c )

Basta trocar esse valor de y na função e ver se z vai ser constante.

y = - x + 2

z = f x , - x + 2 = ln ⁡ e x - x + 2 - 1

z = ln ⁡ e 2 - 1

Que, por mais feio que seja, é uma constante.

Então essa reta é uma curva de nível.

Passo 5

d )

Basta trocar esse valor de y na função e ver se z vai ser constante.

y = - x + 3

z = f x , - x + 3 = ln ⁡ e x - x + 3 - 1

z = ln ⁡ e 3 - 1

Que, por mais feio que seja, é uma constante.

Então essa reta é uma curva de nível.

Passo 6

e )

Como a função representa lucro, queremos o maior valor de z possível. Qual deles é maior?

Sabemos que

e 3 > e 2

Isso porque e ≅ 2,7

Subtrair 1 não vai mudar o cara dentro do logaritmo, então a segunda reta vai ser melhor. A melhor situação é

y = - x + 3

Resposta

  1. x + y = 10

    2. x + y = 1

  2. x + y = a + b
  3. z = ln ⁡ e 2 - 1
  4. z = ln ⁡ e 3 - 1
  5. y = - x + 3

Exercício Resolvido #6

Howard Anton, Irl Bivens, Stephen Davis, Cálculo – Volume II, 8ª ed. Porto Alegre: ARTMED EDITORA S.A, 2005, p. 934 - 37

Em cada parte, as questões se referem ao mapa de contorno na figura abaixo.

a) O ponto A ou B é o ponto mais alto? Explique seu raciocínio.

b) O ponto A ou B está na inclinação mais íngreme? Explique seu raciocínio.

c) Iniciando em A e movendo-se de tal modo que y permanece constante e x cresce, a elevação começará a crescer ou decrescer?

d) Iniciando em B e movendo-se de tal modo que y permanece constante e x cresce, a elevação começará a crescer ou decrescer?

e) Iniciando em A e movendo-se de tal modo que x permanece constante e y decresce, a elevação começará a crescer ou decrescer?

f) Iniciando em B e movendo-se de tal modo que x permanece constante e y decresce, a elevação começará a crescer ou decrescer?

Passo 1

a)

Essa é fácil, basta ver qual é o nível de cada curva! O nível está indicado pelo número ao lado da curva.

Ou seja, o ponto A está numa curva de nível de altura 3 , enquanto o ponto B está na altura 2 .

Portanto, o ponto A é mais alto.

Passo 2

b)

Quanto mais próximas as curvas de nível, mais íngreme a inclinação.

Podemos ver que as curvas de nível em torno de B estão mais próximas, logo o ponto B está na inclinação mais íngreme.

Passo 3

c)

Como já vimos, o ponto A está na altura 3 .

Se partirmos dele mantendo o y constante e fazendo o x crescer, ou seja, pra direita, estaremos caminhando na direção de uma curva de nível de altura 4 .

Portanto, a elevação está crescendo!

Passo 4

d)

Seguindo a mesma lógica da letra anterior, partindo do ponto B   pra direita estamos andando da altura 2 na direção de uma curva de altura 1 : a elevação está decrescendo.

Passo 5

e)

É a mesma coisa! Partindo de A mantendo o x constante e fazendo o y decrescer, estamos andando pra baixo, na direção da mesma curva de nível de altura 4 do item c): a elevação está crescendo.

Passo 6

f)

E agora, pra finalizar, indo do ponto B pra baixo notamos que a elevação está decrescendo: de novo estamos andando de uma curva de nível 2 pra uma de nível 1 .

Resposta

a) A

b) B

c) crescer

d) decrescer

e) crescer

f) decrescer