Introdução aos Limites de Funções de Várias Variáveis
Teoria
Certo, agora vamos voltar a falar de limites.
A ideia é a mesma da função de uma variável: pra qual valor a função tende quando nos aproximamos de certo ponto?
Neste caso, temos e tendendo, simultaneamente, para dois valores independentes. A notação do limite é esta:
Lê-se: limite de quando tende para e para .
No fundo, basta substituir diretamente os valores de e e ver o que acontece.
Por exemplo:
Substituindo os valores:
Só uma observação: as propriedades de soma, multiplicação, “passar o limite pra dentro”, de limites pra funções de 1 variável valem aqui também e pra você não ter que ficar caçando essas propriedades, vou dar uma lembradinha rápida nelas aqui:
E, se for composta, teremos:
Agora vamos ver uns exercícios? :)
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ, P2 2014.2, questão 5 (modificada)
Calcule o limite
Passo 1
Então pessoal, quando vamos resolver um limite de uma função com varias variáveis, o primeiro passo é igual o de quando resolvemos um limite normal: substituir os valores!
Repara que o está tendendo a e o está tendendo a .
Então agora é só substituir o pelo e o pelo . Veja só como fica:
Pronto! Depois de substituir, a gente calcula tudo normal. Resolvendo tudo chegamos que esse limite vai para zero!
Resposta
Exercício Resolvido #2
George B. Thomas, Cálculo – Volume 2, 11ª ed. São Paulo: Pearson Education do Brasil, 2009, p. 304 - 12
Calcule o limite
Passo 1
E ai, pessoal? Tudo bom? Se liga, sempre que a gente for resolver qualquer limite, a nossa primeira tentativa sempre vai ser substituir os valores para saber se já chegamos a um resultado ou caímos em uma indeterminação. Então vamos lá!
Substituindo os valores de e (repara que e ):
Calculando esse cosseno e seno, vamos encontrar:
E é só isso!
Resposta
Exercício Resolvido #3
Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, p.81 – exemplo 3.9
Seja
Calcule
Passo 1
Substituímos os valores:
O que dá:
Resposta
Exercício Resolvido #4
Howard Anton, Irl Bivens, Stephen Davis, Cálculo – Volume II, 8ª ed. Porto Alegre: ARTMED EDITORA S.A, 2005, p. 945 - 28
Determine
Passo 1
Substituindo os valores de e :
Uma função me fornece o valor cuja tagente seja igual a . Repare que o termo dentro da arctangente tende pra .
Deste modo, temos que buscar qual valor cuja tangente vai para o infinito.
Passo 2
Lembra que a função tangente é uma razão de seno e cosseno?
Note, que quando o cosseno for zero, os valores de tangente vão tender ao infinito. E o cosseno é igual a zero, onde é qualquer número inteiro.
Vamos olhar o gráfico da função tangente para entender melhor seu comportamento:
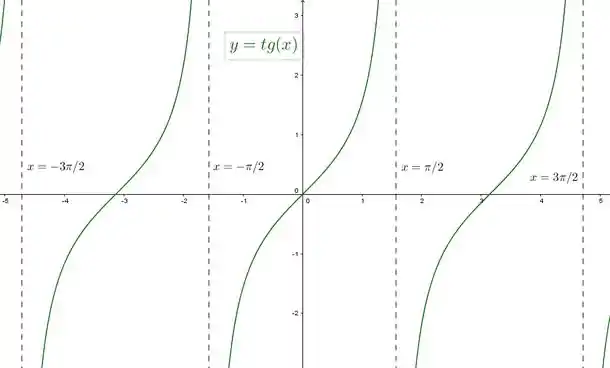
Repara que ela vai para infinito para .
Assim, temos
Botei as aspas porque não dá pra tratar o infinito como se fosse um número! Mas escrevendo a resposta bonitinha, temos que