Parametrizações Avançadas de Superfície
Produzido por Arthur Melo de AlmeidaTeoria
Em parametrização explícita, vimos o que é parametrização e a parametrização de superfícies que podiam ser escritas como .
Agora vamos aprofundar nosso conhecimento aprendendo outras parametrizações importantíssimas! Vale lembrar que qualquer superfície pode ser parametrizada, mas temos que ter cuidado de escolher parâmetros que nos ajude a resolver o problema! Lembre-se: parametrizar superfície, sempre 2 parâmetros.
Em algumas superfícies é muito útil utilizar uma parametrização mais específica. Vamos ver três casos importantes que são: a parametrização de um cilindro, a de uma esfera e a de uma superfície de revolução.
Mas, antes de parametrizar estas superfícies, vamos revisar duas relações trigonométricas importantes!
A primeira é a relação fundamental da trigonometria:
Outra relação muito importante é:
Parametrização de um cilindro
Seja um cilindro de equação . Olha lá, por cilindro entendemos só a parte lateral, não estamos falando das tampas em cima nem embaixo. Então, vamos escolher os seguintes parâmetros:
Mas, não eram para ser em função de dois parâmetros?! Aí os pontos estão em função de e .
Calma! Estamos vendo a equação genérica de um cilindro, então chamamos o raio de , mas ele é um valor constante, não é uma variável. Logo, não é um parâmetro. Olha o exemplo desse cilindro aqui
Parametrização de uma esfera
Agora vamos ver a esfera! Uma esfera genérica tem equação , onde é o raio da esfera. A parametrização esférica usa os parâmetros:
Agora já podemos associar ao cilindro, né? Aconteceu a mesma coisa! aqui é um valor constante, então os parâmetros da esfera são e
Parametrização de uma superfície de revolução
Algumas vezes o seu problema vai te pedir para calcular uma “superfície de revolução”, ou então “a superfície obtida girando a função em torno de algum eixo”. Muita calma nessa hora, jovem! O nome parece difícil de entender, mas esse tipo de questão tem um macete que vai deixar tudo tranquilo! Olha só esse exemplo aqui:
Encontre uma parametrização da superfície resultante da rotação da reta , limitada por , em torno do eixo .
A superfície que o enunciado está se referindo é a seguinte:
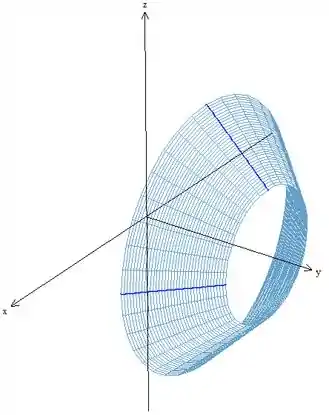
Ok, entendi, mas e ai? Como parametrizo esse tipo de superfície?
É bem simples! Dá para perceber que a “ideia” de eixo e eixo se confunde no problema? Ou seja, se eu começasse pela mesma reta, só que no plano daria na mesma superfície! Por isso, quando rodamos no eixo , as parametrizações de e vão estar associadas! A mesma coisa vai acontecer quando rodarmos nos eixos ou .
No nosso problema, vamos dizer que , com isso, pela equação inicial temos:
E vamos colocar um fator referente ao giro que fizemos com a função.
Perceba que esse fator não entrou no parâmetro de porque giramos em torno dele! Além disso, a função está presente no termo também, isso por causa daquela história de e serem parecidos quando rodamos no eixo , lembra?
Pronto, está parametrizada!
De forma geral...
Rotação no eixo :
Rotação no eixo :
Rotação no eixo :
Parametrização x Mudança de variáveis
Devemos ficar atentos na diferença entre parametrizar uma curva e fazer mudança de variáveis! É muito comum confundir os dois, pois as expressões são realmente parecidas.
Para começar, vimos que na parametrização de superfícies colocamos a função em dois parâmetros. Já na mudança de variáveis, continuamos com três variáveis no problema!
Qual é a conclusão que podemos tirar disso, e isso aqui é muito importante: Quando escrevemos algo com dois parâmetros, isso representa uma superfície! Quando escrevemos algo com três parâmetros, isso representa um sólido! Não vai confundir isso, beleza?
Vamos ver um exemplo?
Sabemos que um sólido esférico de equação é escrito em coordenadas esféricas como:
Com as variáveis definidas no seguinte intervalo,
Ou seja, ao mudar de variáveis o nosso problema sai de para
Agora se pegarmos somente a superfície esférica deste sólido, concorda que a variável não é mais uma variável, é fixa e seu valor é ?
Então, a equação da superfície esférica é e como é fixo e de valor igual a , a superfície só depende das variáveis e (Veja só, dois parâmetros!!) e a função de parametrização é:
Com os parâmetros e variando,
Acho sempre válido explicar aqui, cada parametrização está associada a apenas uma superfície! Da mesma forma que a gente olha pra essa equação e “sabe” que é um plano que passa por , e . Um computador consegue olhar para a parametrização
E saber que o esboço disso é uma esfera de raio centralizada na origem.
Deu para clarear um pouco a diferença? Bom, vamos aos exercícios pra fixar melhor isso aí!!
Parametrização de uma esfera
Parametrização de uma superfície de revolução
Parametrização x Mudança de variáveis
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ, Lista de Parametrização, Questão 4
Parametrize a parte da superfície:
Limitada pelas superfícies:
Passo 1
Vamos começar reescrevendo esta equação e saber qual é a cara dela!
Reescrevendo a equação da superfície, temos:
Completando o quadrado perfeito:
Ajeitando a parte dentro dos parênteses, temos
Ou seja, se trata de um cilindro de raio com centro no ponto .
Agora vamos parametrizar e depois achar os limites para equação parametrizada!
Passo 2
Podemos parametrizar a superfície com coordenadas cilíndricas. Então vamos deixar as componentes em e em função de seno e cosseno. Fica assim:
Substituindo na equação original, podemos achar o :
Repara que o parâmetro sumiu. Pois toda equação multiplicada por é igual a ela mesma. Mas como é uma superfície precisamos necessariamente de dois parâmetros.
Mas fica, tranquilo, como estamos falando de um cilindro no eixo , podemos deixar o sendo o próprio parâmetro e as funções seno e cosseno descrevem a parte circular do cilindro. Logo a parametrização fica assim:
Passo 3
Agora podemos começar a pensar nos limites da superfície. O enunciado disse que ela é limitada pelas superfícies:
Ou seja,
Como acabamos de parametrizar, precisamos colocar em função de . Já sabemos que , então olhando no Passo 1 temos que
Substituindo, ficamos com,
Agora na real já está pronto. Falta só arrumar, mas não é de palhaçada não. Arrumar algebricamente esse tipo de coisa (i.e. limitações da superfície) é algo que vai te ajudar na hora de fazer alguma integral nos próximos capítulos. Arrumando:
E encerrou!
Resposta
Exercício Resolvido #2
Hamilton Luiz Guidorizzi, Um curso de Cálculo – volume 3, 3ª ed. Rio de Janeiro: LTC, 1997, pp. 209 - 3.
Determine uma parametrização para o conjunto de todos tais que
Onde e são constantes estritamente positivas.
Passo 1
A equação que queremos parametrizar é parecida com a equação da esfera , assim, vamos tentar usar a parametrização parecida com a esférica!
Mas antes de usar a parametrização vamos definir novas variáveis que tornem a nossa equação igual a da esfera, assim:
Que quando substituímos na equação que queremos parametrizar temos:
Passo 2
Podemos parametrizar a nova equação com coordenadas esféricas. Segue que:
Com,
Por enquanto a nossa parametrização é:
Mas está não é a superfície que estamos buscando!
Passo 3
Agora podemos voltar para as variáveis e
Assim, temos que a parametrização da nossa curva é:
Resposta
Exercício Resolvido #3
UFRJ, Lista de Exercícios de Parametrização, Questão 5
Parametrize a porção da esfera que não se encontra no interior do paraboloide .
Passo 1
Primeiramente, sabemos que a parametrização de uma esfera é melhor em coordenadas esféricas, então já podemos atacar com a seguinte parametrização:
Onde . Seguindo, temos:
Substituindo :
Podemos seguir com a limitação da esfera, que é estar fora do paraboloide.
Passo 2
Um ponto está fora do paraboloide se ele respeita a inequação:
Como podemos averiguar pelo gráfico:
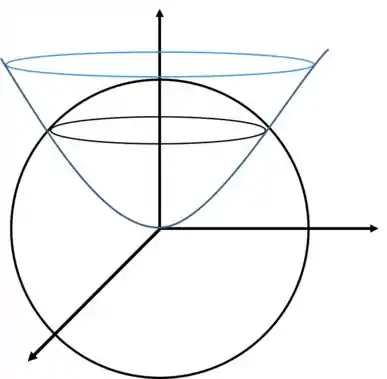
Portanto, arrumando malandramente, somamos em ambos lados:
As raízes são:
Mas como temos um paraboloide deve ser sempre positivo, então eles se encontram em E assim:
De resto o , por sua definição, pode ir até , então:
O não tem restrições, com exceção daquela convencionada pela trigonometria:
Resposta
Exercício Resolvido #4
UERJ - Análise Vetorial - Lista 3 Flávio - 7f
Obtenha uma parametrização para a seguinte superfície:
Passo 1
Primeira pergunta, vocês lembram que superfície é essa? Se não lembram eu vou dar uma ajuda, é um hiperbolóide de uma folha! Alguma coisa assim oh:
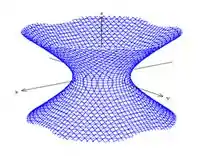
Sacou?
E como ele é formado? Ele é uma hipérbole rotacionada em torno de um eixo!!! No caso, é rotacionada em torno do eixo que está com o sinal negativo (o ). Então estamos parametrizando uma superfície de revolução 😉
Vamos usar como curva a parte de da hipérbole no plano :
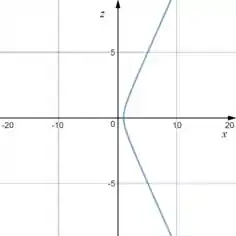
Passo 2
Show, próximo problema! Já sabemos que essa superfície é formada pela revolução de meia hipérbole. Mas como que é a parametrização de uma hipérbole?!?!
Pois é, temos que lembrar disso na hora também, então puxe todos os seus conhecimentos de parametrização de curvas agora! A parametrização é essa aqui oh:
Sendo que essa é só a parte com positivo da hipérbole.
Então para a nossa hipérbole , temos:
Além disso, como e são parecidos quando rodamos em torno de , vai aparecer um no também!
Passo 3
Pra finalizar rotacionamos isso em torno do eixo e ficamos com:
Resposta
Exercício Resolvido #5
Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009 – Modificado
Encontre uma parametrização para a superfície obtida girando-se a circunferência abaixo em torno do eixo :
Passo 1
Já sabemos que, quando aparecer essa história de rodar uma função em torno de algum eixo, estamos tratando de superfície de revolução né? Essa está rodando em torno do eixo , portanto vamos colocar aquele fator de giro nos eixos e .
O gráfico da nossa superfície de rotação é esse aqui:
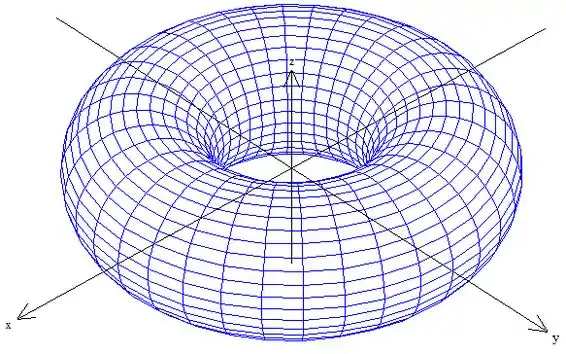
Passo 2
Para conseguir parametrizar a superfície, precisamos antes obter nosso e certo? Vamos ver a nossa equação da circunferência inicial:
Pela relação fundamental trigonométrica
Temos que
Como é o círculo inteiro que está rodando, temos que
Passo 3
Agora só falta substituir tudo na fórmula! Como rodamos no eixo , o fator de giro entra nos eixos e , e a nossa parametrização fica assim: