Parametrização de Superfícies Explícitas
Produzido por Arthur Melo de AlmeidaTeoria
Definição
Antes de aprendermos a integrar em superfícies, precisamos saber como descrevê-las. Uma superfície é um objeto no espaço, assim é natural pensarmos que três variáveis são necessárias para descrevê-la!
Agora imagine a seguinte equação , olhando a figura abaixo, você concorda que ela representa uma superfície?
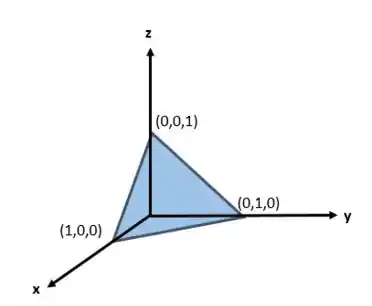
Então, agora que já vimos a superfície vamos pensar o que isto tem a ver com parametrização! Concorda comigo que se eu te der um valor de e um valor de você tem o valor de ? Basta substituir em ! Ou seja, eu não preciso de 3 variáveis para parametrizar uma superfície e sim de 2!
Isto significa que a superfície tem como parâmetros as variáveis e !
Deu para pegar a ideia de parametrização? Se não conseguiu não se preocupe, logo veremos exemplos de parametrização e este assunto vai ficar mais claro! Mas, antes vamos definir parametrização de modo mais formal.
Dizemos, então, que uma superfície é parametrizada por uma função vetorial , tal que:
Dentro de um domínio do plano . Utilizamos e como parâmetros, mas você pode escolher a variável que quiser. Não se assuste com essa notação ela vai ficar mais clara ao longo da teoria.
Parametrização explícita
Este é o tipo mais simples de parametrização! Foi o que usamos acima para demonstrar a ideia de parametrização. Ela ocorre quando uma das variáveis pode ser escrita como função das outras duas:
Muitas vezes usamos este tipo parametrização sem nem mesmo saber!
Exemplo: Vamos analisar a equação do plano e escrever sua forma paramétrica explícita!
Olhando a equação do plano podemos notar que é possível escrever ! Agora vamos encontrar :
Pronto! Encontramos nossa primeira superfície parametrizada! Agora só para terminar, vamos colocar nossa parametrização no formato da função vetorial .
Chamamos e , logo:
Encontrando o domínio dos parâmetros
Ao parametrizar uma superfície devemos ficar bem atentos quanto a mudança do domínio das variáveis. Ih... Acho que não ficou muito claro né?! Vamos tentar simplificar mostrando como fazer com a equação que vimos lá no início, .
Sem definir nenhum domínio este plano é infinito, é válido para qualquer valor de , e . Mas não queremos o plano todo, mas sim uma parte dele. Então, vamos encontrar o domínio da superfície representada na imagem!
Quem está dizendo quais pontos eu estou usando na parametrização são as variáveis concorda? Então se eu falar quais pontos eu quero trabalhar, eu consigo limitar a superfície.
No nosso primeiro exemplo a gente só quer a parte do plano no primeiro octante. A gente consegue impor isso se estiverem dentro desse triângulo aqui:
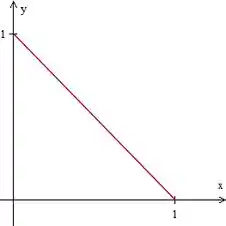
Agora como a gente escreve essa região matematicamente? É igual o que a gente fazia em integrais duplas região do tipo I ou do tipo II. Portanto, podemos dizer que
Então é isso pessoal, quando pedir para parametrizar uma superfície fica ligado se ela pode ser escrita como . Se puder os parâmetros são as variáveis da função. Depois só achar o domínio em que eles vão variar (no nosso caso foi esse triângulo).